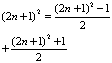九年级数学阶段性测试试卷1

一、填空题（每题3分，共30分）

1、计算: =_________.

2、若分式的值为0，则=_________.

3、纳米是长度计量单位，1纳米=米，则12纳米用科学记数法表示为　　　　　　　米.

4、分式的最简公分母是　　　　__.　

5、一元二次方程的根是__________.

6、已知方程的两根是,则=__________.

7、若关于x的方程的解是正数，则的取值范围是　　  　 

8、已知是一元一次方程的一个根，则m的值为　　　　　

9、某商品标价1375元，打八折出售，仍可获利10%，则该商品的进价是　　　 　元

10、观察下列等式=25=12+13，=49=24+25，=81=40+41，=121=60+61，这些等式反映自然数间的某种规律，设表示自然数，试用关于的等式表示出你所发现的规律_______________________.

二、选择题（每题3分，共30分）

11、下列各式中属于分式的有--------------------------------------------------------------------( 　　　)

（１）（２）（３）（４）（５）

Ａ、１个　　　　　　 Ｂ、２个　　　　　 Ｃ、３个　　　　 Ｄ、４个

12、下列运算正确的是----------------------------------------------------------------------------(　　　 )

Ａ、　　　Ｂ、　　 Ｃ、　　Ｄ、

13、以和为根的一元二次方程是------------------------------------------(　　　 )

Ａ、　　　　　　　　　　 Ｂ、　

Ｃ、　　　　　　　　　　 Ｄ、

14、如果m个人完成一项工作需要d天，则(m+n)个人完成这项工作需要的天数为

　　---------------------------------------------------------------------------------------------------(　　　 )

Ａ、　　　　　 Ｂ、　　　　　 Ｃ、　　　 Ｄ、

15、计算的结果是----------------------------------------------------(　　　 )

Ａ、　　　　　 Ｂ、　　　　  Ｃ、　　　　  Ｄ、

16、下列说法正确的是---------------------------------------------------------------------------(　　　 )

Ａ、方程是关于的一元二次方程

Ｂ、方程的常数项是４

Ｃ、若一元二方程的常数项为０，则０必是它的一个根。

Ｄ、当一次项系数为０时，一元二次方程总有非零解。

17、若方程有增根，则m的值为---------------------------------(　　　 )

Ａ、　　　　　　　　　　　　　　  Ｂ、　

Ｃ、或　　　　　　　　　　 Ｄ、或

18、方程的根的情况是--------------------------------------------------------(　　　 )

Ａ、有两个不相等的实数根，

Ｂ、有两个相等的实数根。

Ｃ、没有实数根。

Ｄ、无法确定。

19、党的十六大提出全面建设小康社会，加快推进社会主义现代化，力争国民生产总值到2020年比2000年翻两番（４倍）。在本世纪的头二十年（2001年――2020年），要实现这一目标，以十年为单位计算，设每个十年的国民生产总值的平均增长率都是，那么满足的方程为------------------------------------------------------------------------(　　　 )

Ａ、　　　　　　　　　　　　  Ｂ、　　　

Ｃ、　　　　　　　　　　　　　  Ｄ、

２０、已知，是方程的两根，且则m的值是---(　　　 )

Ａ、16　　　　　　  Ｂ、18　　　　　　　 Ｃ、18或0　　　　　 Ｄ、16或0

三、解答题（第21题6分，22题8分，23题6分，24－27题各10分，共60分）

21、先化简后求值

，其中。

22、解方程

（1）　　　　　　（2）

23、已知x关于的方程有两个不相等的实数根。

（1）求k的取值范围。

（2）是否存在实数k，使此方程两个实数根的倒数和等于０？若存在，求出k的值；若不存在，说明理由。

24、基商店经销一种销售成本为每千克40元的水产品，根据市场分析，若按每千克50元销售，一个月能售出500千克，销售单价每涨一元，月销售量就减少数10千克，针对这种情况，请解答以下问题。

（1）当销售单价为每千克55元时，计算月销售量和月销售利润。

（2）设销售单价为每千克元，月销售利润为元，求与的函数关系式。

（3）在月销售成本不超过10000元的情况下，使月利润达到8000元，销售单价应定为多少？

25、已知一元二次方程有两个不相等的实数根，如果k是符合条件的最大整数，且一元二次方程与有一个相同的根，求此时m的值。

26、阅读下列材料：

先观察，寻找出规律后，再解答下列各题：

，，，

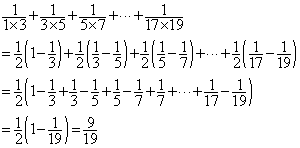
（1）在式子　中，第６项是____________, 第n项是______________.

 

 

（2）上述表示和的方法是将每一个分数化成两个分数的差，使得除首末两项外的中间各项

均可以消去，从而达到求和的目的，受此启发，试一试，解方程：

27、阅读材料：已知，且，

求的值。

解：由及知

又　

可变形为

由和

所以p与是方程的两个不相等实数根。

则　  

根据阅读材料所提供的方法，完成下面的解答：

已知：,且

求的值。

九年级数学阶段性测试试卷

参考答案

一．填空题

题号	1	2	3	4	5
答案		1
题号	6	7	8	9	10
答案				1000

二．选择题

题号	11	12	13	14	15	16	17	18	19	20
答案	C	B	A	C	B	C	C	C	B	D

三．解答题

21．，其中

解：原式=------------------------------------------------------------------2分

　　　　=----------------------------------------------------------------------------4分

　　当时，原式==------------------------------------6分

22． (1) 　　　　　　　　　　　 (2)

　　 解：　　　　　　　　　　　  解：--------------------------4分

　　　　 ---------------------4分　　　　　  （无检验扣2分）

23. 解: (1)由题意可知：且---------------------2分

　　　　　　　　　　　　 解得　且-----------------------------------3分

　　　(2)设是该方程的两根，并假设满足题意的存在

　　　　 则　　　 ----------------------------------4分

　　　　　　　　   ---------------------------5分

　　　　　　　　　　  解得　

　　　　　　　　　　  不满足（1）中的条件

　　　　　　　　  满足题意的不存在。--------------------------------------------6分

24. 解: (1) 销售量：（千克）-----------------------------1分

　　　　  月销售利润：（元）-------------------------------2分

　　　(2)

　　　　  -----------------------------------------------------6分

　　　(3)设销售单价为每千克元，

　　　　 则根据题意得 ①　 -----------------7分

　　　　　　　　　 且 ②　 --------------------8分

　　　　　　　　　 由①得　 　　

　　　　　　　　　 由②得　 ----------------------------------------------9分

　　　　  综上所述，-----------------------------------------------------------------10分

25. 解:  一元二次方程有两个不相等的实数根

　　　  

　　　　　　　 ---------------------------------------------------------------------------3分

　　　  符合条件的最大整数--------------------------------------------------------4分

　　　  方程的两根为---------------------------------6分

　　　　  当一个相同的根为1时，求得-------------------------------------------8分

　　　　  当一个相同的根为3时，求得----------------------------------------10分

26. (1) ,　------------------------------------------------------------4分

　 (2) 解: 可将原方程化为：

　　　　　 -----------------6分

　　　　　　　　　　　　　　　　　　　　　 

　　　　　　　　　　　　　　　 可化为　　　　

　　　　　　　　　　　　　　　 解得　　　　 -----------------8分

　　　　　　　　　  经检验，是增根，舍去

　　　　　　　　  原方程的根是-----------------------------------------------10分

27. 解: 由,知--------------------------------------2分

　　　　方程可变形为：

　　　　　　　 --------------------------------------------------------------4分

　　　又

　　　　 --------------------------------------------------------------------------------5分

　　　　 是方程的两个不等实根-------------------------------8分

　　　　 -------------------------------------------------------------------------10分