九年级数学竞赛训练题
班级：_______ 姓名：______ 得分：_______
一、选择题:（3分×10=30分）
1．关于x的一元二次方程x2＋kx－1=0的根的情况是
A、有两个不相等的同号实数根 B、有两个不相等的异号实数根
C、有两个相等的实数根 D、没有实数根
2．若x>2，化简
的结果是（ ）
A．x+2 B．±（x-2） C．2-x D．x-2
3．用配方法将二次三项式a2+4a+5变形，结果是（ ）
A．（a-2）2+1 B．（a+2）2+1 C．（a-2）2-1 D．（a+2）2-1
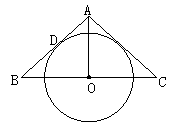
4．已知△ABC中，AB=AC，∠A=50°，⊙O是△ABC的外接圆，D是优弧BC上任一点（不与A、B、C重合），则∠ADB的度数是（ ）
A．50° B．65° C．65°或50° D．115°或65°
5．小明所在的年级共有10个班，每个班有45名学生，现从每个班中任抽一名学生共10名学生参加一次活动，小明被抽到的概率为（ ）
A．
B．
6．某校去年对实验器材的投资为2万元，预计今明两年的投资总额为8万元，若设该校这两年在实验器材投资上的平均增长率为x，则可列方程____ __．
7．已知AB是两个同心圆中大圆的弦，也是小圆的切线，设AB=a，用a表示这两个同心圆中圆环的面积为（ ）
A．
a2 B．
a2 C．
a2 D．
a2
8．已知半径为1的圆心在原点，半径为3的圆的圆心坐标是（-
，1），则两圆位置关系是（ ）
A．外切 B．内切 C．相交 D．外离
9．用一把带有刻度的直角尺，①可以画出两条平行的直线a与b，如图（1）；②可以画出∠AOB的平分线OP，如图（2）；③可以检验工作的凹面是否成半圆，如图（3）；④可以量出一个圆的半径，如图（4）．
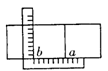
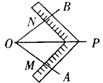
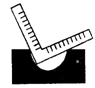
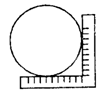
(1) (2) (3) (4)
上述四个方法中，正确的个数是（ ）
A．1个 B．2个 C．3个 D．4个
二、填空题（3分×10=30分）
11．若代数式
有意义，则x______．
12．计算（2
-3）2006·（2+3）2006=_______．
13．方程（x-1）=（x-1）的根为_______．
 | |||
 | |||
(6) (7) (8)
14．如图6，⊙O的半径为5cm，圆心O到AB的距离为3cm，则弦AB长为_______．
15．等边三角形ABC绕着它的中心，至少旋转______度才能与它本身重合．
16．如图7，在△ABC中，∠C=90°，AB=10，AC=8，以AC为直径作圆与斜边交于点P，则BP的长为_______．
17．制造一种产品，原来每件的成本是100元，由于连续两次降低成本，现在的成本是81元，则平均每次降低成本的百分率为_______．
18．如图8，已知一扇形的半径为3，圆心角为60°，则图中阴影部分的面积为________．
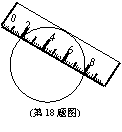
18．如图，一宽为2cm的刻度尺在圆上移动，当刻度尺的一边与圆相切时，另一边与圆两个交点处的读数恰好为“2”和“8”(单位：cm)，则该圆的半径为 cm。
 | |||
 | |||
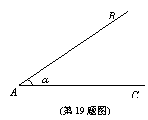
19．如图，∠BAC=30°，AB=10。现请你给定线段BC的长，使构成△ABC能惟一确定。你认为BC的长可以是 ， 。
三、解答题（60分）
21．计算下列各式（每小题3分，计12分）
（1）（+1）2 （2）（+1）（-1）
22．（6分）化简后求值:已知a=2-，b=2+，求
的值．
23．（6分）抛掷两个普通的正方体骰子，把两个骰子的点数相加，则“第一个骰子为1、第二个骰子为6”是“和为7”的一种情况，我们可以将它记为（1，6）．如果一个游戏规定，掷出“和为7”时甲方赢，掷出“和为9”时乙方赢，请预测甲乙双方获胜的概率各是多少？
24．（7分）黄冈百货商店服装柜在销售中发现：“宝乐”牌童装平均每天可售出20件，每件盈利40元，为了迎接“六．一”国际儿童节，商场决定采取适当的降价措施，扩大销量，增加盈利，减少库存，经市场调查发现：如果每件童装每降价4元，那么平均每天就可多售出8件，要想平均每天在销售这种童装上盈利1200元，那么每件童装应降价多少元？
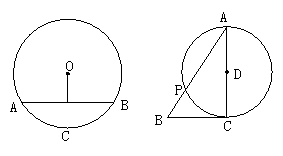
25．（6分）如图，AO是△ABC的中线，⊙O与AB相切于点D．
（1）要使⊙O与AC边也相切，应增加条件_________．
（2）增加条件后，请你证明⊙O与AC相切．
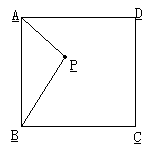27．（7分）如图，P为正方形ABCD内一点，将△APB绕点B按逆时针方向旋转90°得到△BP′M，其中P与P′是对应点．
（1）作出旋转后的图形；
（2）若BP=5cm，试求△BPP′的周长和面积．
22．(本小题满分12分)
如图7
⊙0的半径为1，过点A(2，0)的直线切⊙0于点B，交y轴于点C.
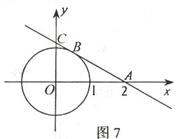(1)求线段AB的长；
(2)求以直线AC为图象的一次函数的解析式．