九年级数学期中测试卷
一、选择题(每小题3分,共36分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
1．
当a〈３时，下列式子
，其中，一定有意义的个数为（ ）
Ａ １ Ｂ ２ Ｃ ３ Ｄ ４
２．下列各式中是最简二次根式的是（ ）
Ａ 
Ｂ 
Ｃ 
Ｄ 
３．下列二次根式中能与
进行合并的是（ ）
Ａ 
Ｂ 
Ｃ 
Ｄ 
４．已知a〈0，则
化简后为（ ）
Ａ 
Ｂ 
Ｃ 
Ｄ 
５．若
，则a+b+ab的值为（ ）
Ａ 
Ｂ 
Ｃ －５ Ｄ ３
６．已知２是关于ｘ的方程
的一个根，那么１－２ａ的值为（ ）
Ａ－５ Ｂ－３ Ｃ ３ Ｄ ７
７．方程３ｘ２＋２ｘ－５＝０的根的情况是（ ）
Ａ有两个相等的实数根 Ｂ有两个不相等的实数根
Ｃ没有实数根 Ｄ只有一个实数根
８．方程２ｘ（ｘ－３）＝４（３－ｘ）的根为（ ）
Ａ ｘ＝２ Ｂ ｘ＝－２ Ｃ ｘ１＝２ｘ２＝３ Ｄ ｘ１＝－２ｘ２＝３
９．若关于ｘ的一元二次方程２ｘ（ｋｘ－４）－ｘ２＋６＝０没有实数根，则k的最小整数值为（ ）Ａ －１ Ｂ １ Ｃ ２ Ｄ ３
１０。若ｘ１，ｘ２是一元二次方程３ｘ２＋ｘ－１＝０的两个根，则
的值为（ ）
Ａ １ Ｂ －１ Ｃ ３ Ｄ －３
１1。餐桌桌面是第１６０ｃｍ宽１００ｃｍ的长方形，王阿姨准备设计一块桌布，面积是桌面的２倍，且使四周垂下的边宽相等，小红设四周垂的边宽是ｘｃｍ，那么满足ｘ的方程为（ ）
Ａ（１６０＋ｘ）（１００＋ｘ）＝２×１６０×１００
Ｂ（１６０＋２ｘ）（１００＋２ｘ）＝２×１６０×１００
Ｃ（１６０＋ｘ）（１００＋ｘ）＝１６０×１００
Ｄ（１６０ｘ＋１００ｘ）＝１６０×１００
12．如果a，b是两个不相等的实数,且满足ａ２－３ａ＝１，ｂ２－３ｂ＝１,那么a2+b2的值是（ ）
A 11 B 9 C 7 D 3
二、填空题（每小题3分，共24分）
１３。当ｘ 时，代数式
有意义．
１４。已知
在实数范围内等式成立，则ｘｙ＝ ．
１５。当x= 时，最简二次根式
与
可以合并．
１６。当
时，代数式
的值等于
。
１７。已知方程ｘ２＋ｋｘ－６＝０的一个根是２，则它的另一个根是 ，ｋ的值是 。
１８。若方程
，则ｐ= ，ｑ= 。
１９。已知关于的一元二次方程２ａ（１－ｘ）＝ｂ（１－ｘ２）的实数根，则ａ与ｂ的关系是 ．
２０。已知三角形两边的长分别为６和８，第三边的长是一元二次方程ｘ２－１６ｘ＋６０＝０的实数根，那么这个三角形的面积是
三、解答题（60分）
21．（8分）
（1）
（2）
（3）
（4）
２２。（１０分）解下列各方程
（１）（２ｘ－１）２－９＝０ （２）（２ｘ＋３）２＝５（３＋２ｘ）
（３）３ｘ２＋２ｘ－４＝０ （４）ｘ２－６ｘ＝１ （５）２（３ｘ－１）２－１４＝３ｘ
２３。（５分）计算
２４。（５分）若关于的一元二次方程ｘ２＋（ｍ＋１）ｘ＋ｍ＋４＝０两实根的平方和为２，求ｍ的值
解：设方程的两实根为ｘ１，ｘ２，那么ｘ１＋ｘ２＝ｍ＋１，ｘ１ｘ２＝ｍ＋４
∴ｘ１２＋ｘ２２＝（ｘ１＋ｘ２）２－２ｘ１ｘ２＝（ｍ＋１）２－２（ｍ＋４）＝ｍ２－７＝２
即 ｍ２＝９ 解得，ｍ＝３，ｍ的值是３，请把上述解答过程的错误或不完整之处，写在横线上，并给出正确的解答
错误或不完整之处有： ．
 |
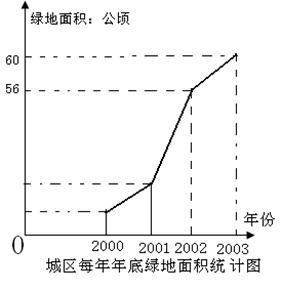
２５。（８分）请你仔细观察图－１，思考下列问题：美化城市，改善人们的居住环境已成为城市建设的一项重要内容，某市城区近几年来，通过拆旧房，植草，栽树，修建公园行措施，使城区绿地面积不断增加
（１）根据图中所提供的信息回答下列问题：２００３年底的绿地面积为 公顷，比２００２年底增加了 公顷，在２００１年，２００１年，２００３年这三年中绿地面积增加最多的是 年
（２）为满足城市发展的需要，计划到２００６年底使城区绿地总面积达到７２．６公顷，度求２００４年，２００５年这两年绿地面积的年平均增长率
26．（6分）某水果批发商场销售一种高档水果，如果每千克盈利10元如果每天可售出500ｋｇ经市场调查发现，在进货价不变的情况下，若每千克涨价1元，日销售量将减少20ｋｇ，现该商场要保证每天盈利6000元，同时又要使顾客得到实惠，那么每千克应涨价多少元？
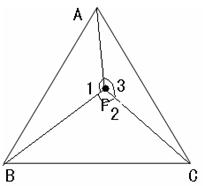
27．如图，在等边△ABC中有一点P连接PA、PB、PC，∠1：∠2：∠3＝3：4：5，且
PA＝6cm
求PB、PC的长
28．（6分）先阅读理解，再回答下列问题
因为
，且
，所以
的整数为1；因为，
且，
所以
整数为2因为
，且
，所以
的整数为3 。。。。。。
以此类推，
（ｎ为正整数）的整数部分为什么?请说明理由: