九年级数学月考测试卷
| 题 号 | 一 | 二 | 三 | 总分 | ||||||
| 1-10 | 11-18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | ||
| 得 分 | ||||||||||
一、 仔细选一选（本题有10个小题，每小题4分,共40分.）
1、在行程问题中，路程s（千米）一定时，速度v（千米/时）关于时间t（小时）的函数关系的大致图像是（ ）
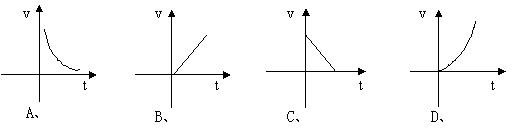
2、若将函数y=2x2的图象向左平移3个单位，再向上平移7个单位，可得到的抛物线是（ ）
A、y=2(x-3)2-7 B、y=2(x-3)2+7 C、y=2(x+3)2-7 D、y=2(x+3)2+7
3、在比例尺为
的地图上，若某建筑物在图上的面积为50 cm2，则该建筑物实际占地面积为（ ）
A、50 m2 B、5000 m2 C、50000 m2 D、500000 m2
4、 如果两点
（1，
）和
（2，
）都在反比例函数
(k>0)的图象上，那么（ ）
A．＜＜0 B．
＜
＜0 C．＞＞0
D．＞＞0
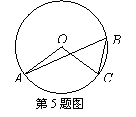
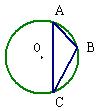
5、如图，A、B、C是⊙O上的三点，∠AOC=100°，则∠ABC的度数为
A、30° B、45° C、50° D、60°
6、二次函数y=ax2+bx+c的图象如图所示，对称轴x=1，下列结论中，正确的（ ）
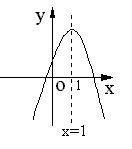A、ac>0 B、b<0
C、b2-4ac<0 D、2a+b=0
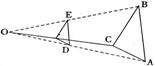
7、按如下方法，将△ABC的三边缩小的原来的
，如图，任取一点O，连结AO、BO、CO，并取它们的中点D、E、F，得△DEF，则下列说法正确的个数是( )
①△ABC与△DEF是位似图形 ②△ABC与△DEF是相似图形
③△ABC与△DEF的周长比为1:2 ④△ABC与△DEF的面积比为4:1
A、1 B、2 C、3 D、4
第7题图 第8题图 第9题图
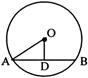
8、如图，已知⊙O的半径为5
，弦
，则圆心O到AB的距离是 【 】
A．1 B．2 C．3 D．4
9、如图，
的边长都大于2，分别以它的顶点为圆心，1为半径画弧（弧的端点分别在三角形的相邻两边上），则这三条弧的长的和是（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
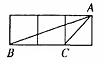
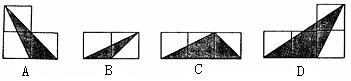
10、如图，小正方形的边长均为l，则下列图中的三角形(阴影部分)与△ABC相似的是( )。
二、认真填一填（本题有8个小题，每小题5分,共40分.）
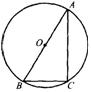
11、如图，AB是⊙O的直径，则∠C= ．
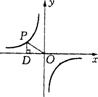
12、如图，点P是反比例函数
上的一点，PD⊥
轴于点D，则△POD的面积为 。
13、二次函数
的对称轴是
14、如图，在⊙O中，弦AB=1.8cm，圆周角∠ACB=30O，则⊙O的直径等于 cm。
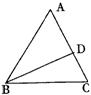
15、如图，D是△ABC的边AC上一点，若AB＝AC，要使△CDB∽△BAC，只需添加条件______________________(只添一个即可)。
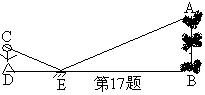16、为了测量校园水平地面上一棵不可攀的树的高度，学校数学兴趣小组做了如下的探索：根据《科学》中光的反射定律，利用一面镜子和一根皮尺，设计如下图所示的测量方案：把一面很小的镜子放在离树底（B）8.4米的点E处，然后沿着直线BE后退到点D，这时恰好在镜子里看到树梢顶点A，再用皮尺量得DE=2.4米，观察者目高CD=1.6米，则树（AB）的高度约为________
米。（精确到0.1米）。
17、请写出一个开口向上，对称轴为直线x=2，且与y轴的交点坐标为(0，3)的抛物线的解析式 。
18、已知点C是线段AB的黄金分割点，且AC>BC，AB=2，则BC= .
三、全面答一答（本题有7个小题，共70分.）
19、（本题满分8分）反比例函数经过点（l, -1).
（1）求k的值
（2）若反比例函数的图象经过点P（a, a-2）, 求a的值．
20、（本题满分8分）如图，在△ABC中，DE//BC，AD=4㎝，DB=2㎝
(1) 
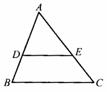求
的值
(2) 如果△ADE的面积是16㎝2，那么梯形BCED的面积是多少？
21、（本题满分10分）如图，已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C。
（1）用直尺画出该圆弧所在圆的圆心M的位置；（4分）
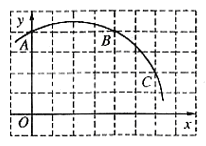（2）若A点的坐标为（0，4），D点的坐标为（7，0），试验证点D是否在经过点A、B、C的抛物线上；（6分）
22．（本题满分10分）如图，BE是△ABC的外接圆⊙O的直径，CD是△ABC的高。
（1） 
求证：
（2） 已知：CD=6，AD=3，BD=8，求⊙O的直径BE的长。
23．（本题满分10分）马戏团让狮子和公鸡表演跷跷板节目．跷跷板支柱AB的高度为1.2米．
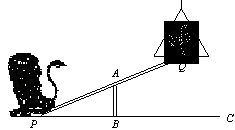（1）若吊环高度为2米，支点A为跷跷板PQ的中点，狮子能否将公鸡送到吊环上？为什么？
（2）若吊环高度为3.6米，在不改变其他条件的前提下移动支柱，当支点A移到跷跷板PQ的什么位置时，狮子刚好能将公鸡送到吊环上？
24．（本题满分12分）某商场购进一种单价为40元的篮球，如果以单价50元出售，那么每月可售出500个，根据销售经验，售价每提高1元，销售量相应减少10个；
（1）假设销售单价提高元，那么销售每个篮球所获得的利润是
元；这种篮球每月的销售量是
个；（用含的代数式表示）（4分）
（2）8000元是否为每月销售这种篮球的最大利润？如果是，请说明理由；如果不是，请求出最大利润，此时篮球的售价应定为多少元？（8分）
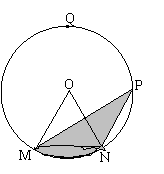
25(本题满分12分)如图，在半径是2的⊙O中，点Q为优弧MN的中点，圆心角∠MON=60°在劣弧QN上有一动点P，且点P到弦MN的距离为。
⑴求弦MN的长；(3分)
⑵试求阴影部分面积
与的函数关系式，并写出自变量的取值范围；(6分)
⑶试分析比较，当自变量为何值时，阴影部分面积与
的大小关系(3分)