九年级
秋半期教学质量检测数学试卷
（全卷共三大题，满分150分，120分钟完卷）
| 题号 | 一 | 二 | 三 | 总分 | 核分人 |
| 得分 |
|
|
|
|
|
|
1．下列各方程中，是一元二次方程的为（ ）
A．x2+
B．3x+4=0
C．4x2+2y－1=0 D．
2．已知一元二次方程x2－2x－m=0，用配方法解该方程，配方后的方程是（ ）
A．（x－1）2=m2+1 B．（x－1）2=m－1
C．（x－1）2=1－m D．（x－1）2=m+1
3．用反证法证明“三角形中必有一个内角不小于60°”，应先假设这个三角形中（ ）
A．有一个内角小于60° B．每一个内角小于60°
C．有一个内角大于60° D．每一个内角大于60°
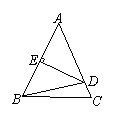
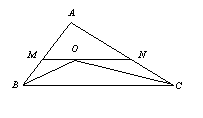4．如图，在△ABC中，∠B与∠C的平分线相交于O点，过O点作MN∥BC交AB于M，交AC与N，若AB=12，BC=24，AC=18，则△AMN的周长为（ ）
A．30
B．33
C．36
D．39
5．某市在“旧城改造”中计划在市内一块如图所示的三角形空地上种植某种草皮以美化环境，已知这种草皮每平方米售价a元，则购买这种草皮至少需要（ ）
A．450a元
B．225a元
C．150a元
D．300a元
6．已知△ABC中，∠C=90º，∠A=30º，BD平分∠B交AC于点D，则点D（ ）
A．是AC的中点 B．在AB的垂直平分线上
C．在AB的中点 D．不能确定
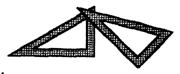7．如图，用两块全等的含30°角的三角板拼成形状不同的平行四边形，最多可以拼成（ ）
A．1个 B．2个
C．3个 D．4个
8．若函数y=
的图象过点（3，-7），那么它一定还经过点（ ）
A.（3，7） B.（-3，-7） C.（-3，7） D.（2，-7）
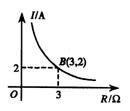9．某闭合电路中，电源电压为定值，电流I（A）与电阻R（Ω）
成反比例，右图表示的是该电路中电流I与电阻R之间函数关
系的图像，则用电阻R表示电流I的函数解析式为（ ）
A．I=
B．I=－
C．I=
D．I=
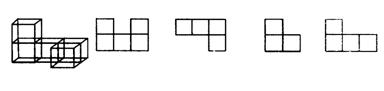10．把5个小正方体搭成如图所示的几何体，从各个不同的方向观察这个几何体，可能看到的视图有（ ）
① ② ③ ④
A．①② B．②③④ C．②④ D．①③④
|
共25分）
11．等腰三角形中有一个角是100°，则其它两角的度数为 。
12．在我国南宋数学家杨辉所著的《田亩比类乘除算法》中有这样一道题：“直田积（矩形面积）八百六十四步（平方步），只云阔（宽）不及一十二步（宽比长少一十二步），问阔 步，长 步.
13．一个人从山下沿30°角的坡路登上山顶，共走500米，那么这座山坡的高度是 。
14．如图，在△ABC中，AB=AC，∠A=50°，
AB的垂直平分线DE交AC于D，则∠DBC
的度数是 。
15．等腰梯形下底边长是13，高为
，上底与腰成120°的角，则这个梯形的中位线长是
。
|
16．解下列方程。（每小题6分，共18分）
①2（x－3）2=x2－9（分解因式法） ②（x－2）（3x－5）=1（用公式法）
③6x2－7x+1=0（用配方法）
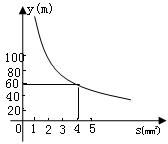
17（本题8分）你吃过拉面吗？实际上在做拉面的过程中就渗透了数学知识：一定体积的面团做成拉面，面条的总长度y(m)是面条的粗细(横截面积) s
(mm
)的反比例函数，其图象和数据如图所示。
⑴写出y与s的函数关系式；
⑵求当面条粗1.6 mm时，面条的总长度是多少米？
 |
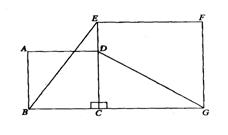
18．（9分）已知：如图1－4－3，AB和DE是直立在地面上的两根立柱．AB=5
，某一时刻AB在阳光下的投影BC=3．
（1）请你在图1—4—3中画出此时DE在阳光下的投影；
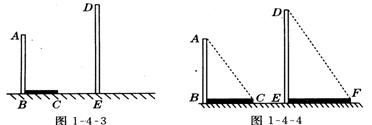（2）在测量AB的投影时，同时测量出DE在阳光下的投影长为6，请你计算DE的长．
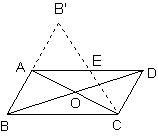
19．（10分）如图，在平行四边形ABCD的纸片中，AC⊥AB，AC与BD相交于O，将△ABC沿对角线AC翻转180°，得到
；
（1）求证：以A、C、D、
为顶点的四边形是矩形；
（2）若四边形ABCD的面积S＝12
， 求翻转后纸片部分的面积，即
；
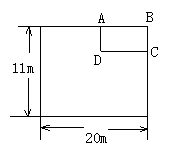
20、（本题10分）某单位为响应政府发出的全民健身的号召,打算在长和宽分别为20m和11m的矩形大厅内修建一个60m的矩形健身房ABCD.
该健身房的四面墙壁中有两侧沿用大厅的旧墙壁(如图为平面示意图),已知装修旧墙壁的费用为20元/ m,新建(含装修)墙壁的费用为80元/ m.设健身房的高为3m,一面旧墙壁AB 的长为xm,修建健身房墙壁的总投入为y元.
(1)求y与x的函数关系式;
(2)为了合理利用大厅,要求自变量x必须满足条件:8≤x≤12, 当投入的资金为4800元时,问利用旧墙壁的总长度为多少?
21．（10分）如图，正方形ABCD的边CD在正方形ECGF的边CE上，连结BE、DG，
（1）观察猜想BE与DG之间的大小关系，并证明你的结论；
（2）图中是否存在通过旋转能够互相重合的两个三角形？若存在，请说出旋转过程；若不存在，请说明理由。
22．（10分）某商场将销售成本为30元的台灯以40元的价格售出，平均每月销售600个，市场调查表明：这种台灯的售价每上涨1元，其月平均销售数量将减少10个，若销售利润率不得高于100%，那么销售这种台灯每月要获利10000元，台灯的售价应定为多少元？
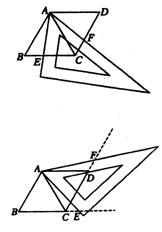
23．（10分）用两个全等的等边三角形△ABC和△ACD拼成菱形ABCD。把一个含60°角的三角尺与这个菱形叠合，使三角尺的60°角的顶点与点A重合，两边分别与AB、AC重合。将三角尺绕点A按逆时针方向旋转。
（1）当三角尺的两边分别与菱形的两边BC，CD相交于点E，F时（如图），通过观察或测量BE，CF的长度，你能得出什么结论？并证明你的结论；
（2）当三角尺的两边分别与菱形的两边BC，CD的延长线相交于点E，F时（如图），你在（1）中得到的结论还成立吗？简要说明理由。
 |