九年级上册数学期中测试题
班级： 姓名： 得分：
一、选择题（每题3分，共30分）
1. 若函数y=（n-2) 
是反比例函数，则n为 ( )
A . ±2 B. 2 C. -2 D. 以上都不对
2. 数2和8的比例中项为 ( )
A. 4 B. ±4 C. 6 D. ±6
3. 如图，在平行四边形ABCD中，点E是CD的中点，连结AE并延长与BC的延长线交于点F．若CF:FB等于 ( )
A. l : 2 B. 2 : 3 C. 1 ; 3 D. 2 : 5
4. 已知扇形的弧长为2Л，半径为4,则此扇形的面积为(
)
A.8π B.6π C. 5π D. 4π
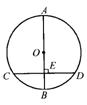
5. 如图，AB是⊙O的直径，AB⊥CD, AB=10,CD=8, 则BE为（ )
A. 2 B. 3 C . 4 D.3.5
6. 抛物线y=3x2+1先向上平移2个单位，再向左平移2个单位所得的解析式为( )
A. y=3(x-2)2-1 B. y=3(x+2)2-1 C. y=3(x-2)2+3 D. y=3(x+2)2+3
7. ⊙O的半径为10cm ,弦AB//CD, 且AB=12cm,CD=16cm,则AB和CD的距离为( )
A. 2cm B.14 cm C. 2cm或14cm D.10cm或20cm
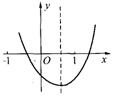
8. 已知二次函数y =ax2+bx+c的图象如图所示，那么下列判断中不正确的是（ )
A. abc >
0 B. b2-4ac
> 0 C.2a+b> 0
D.4a-2b+c<0
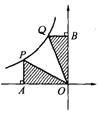
9. 若反比例函数y =
，如图，P, Q为任意两点，SOAP记为S1, S△OBQ记为S2,则（ ）
A.S1 =S2 B. S1 > S2 C. S1 <S2 D．无法判断
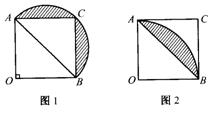10. 如图，OBCA为正方形，图1是以AB为直径画半圆，阴影部分面积记为S1，图2是以O为圆心，OA长为半径画弧，阴影部分面积记为S2 ,则（ )
A. S1 < S2 B. S1 = S2 C. S1 > S2 D．无法判断
二、填空题（每题3分，共30分）
11.若
，则a:b= .
12.反比例函数
经过点(2,3),则k= ．
13.如图，∠BOC=800,则∠A= .
14.二次函数y=2(x-1)2十1的对称轴是 .
15.如图，DE//BC,AD:DB=2:1,若DE=4,则BC= ．
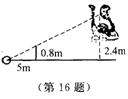16.小芳在打网球时，为使球恰好能过网（网高为0.8m
）且落在
对方区域离网 5m的位置处，已知她击球的高度是2.4m，则她
应站在离网的
m处.
17.若抛物线y=x2-6x+c的顶点在x轴，则c= .
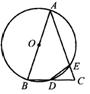
18.如图，等腰△ABC的底边BC的长为4cm，以腰AB为直径的⊙O交BC于点D，
交AC于点E，则DE的长为 cm.
19.已知点(1，3)是双曲线y=
与抛物线y=x2+(k+1)x+m的交点，则k的值等于 。
20.圆锥的底面半径是3cm，高是4cm，则它的侧面积是 。
三、解答题（共40分）
21. 已知线段AB,用直尺和圆规作出它的黄金分割点。（5分）
A
B
22. 如图，AB//CD,AD与BC相交于点O，
．若OA=7cm,求OD的长度.（5分）
23. 反比例函数经过点（l, 2).（7分）
（1）求k的值
（2）若反比例函数的图象经过点P（a, a-1), 求a的值．
24. 如图，在⊙O中，
＝ 600，AB=6cm.(7分)
(1）求圆的半径； 
(2）求阴影部分的面积．
25.已知抛物线 y=-x2+ax+b 经过点A (1,0), B(O，-4). （8分）
(l）求抛物线的解析式；
(2）求此抛物线与坐标的三个点连结而成的三角形的面积．
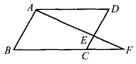
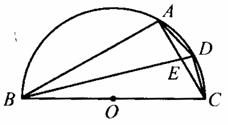
26.如图，BC为半圆的直径为10cm，O为圆心， D是弧
的中点，四边形ABCD的对角线AC,BD交于点E， 弧AD的度数为15度. (8分)
(l）求弧AB的长。
(2)△ABE与△DBC是否相似，并请你说明理由．
四、附加题（10分）
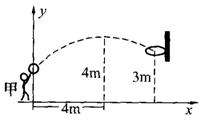
27、27. 某校九年级的一场篮球比赛中，如图队员甲正在投篮，已知球出手时离地面
高
m，与篮圈中心的水平距离7m．当球出手后水平距离为4m时到达最
大高度4m，设篮球运行的轨迹为抛物线，篮圈距地面3m.
(l）建立如图的平面直角坐标系，求出此轨迹所在抛物线的解析式．
(2）问此球能否准确投中？
(3）此时，若对方队员乙在甲前面2m 处跳起盖帽拦截，已知乙的最大摸高
为3.lm，那么他能否拦截成功？为什么？
