九年级上学期期末数学测试题

九年级上学期期末数学测试题

一、选择题:(每题2分，共20分)

  1．化简a的结果是(　)

　　A．

  2．在二次根式①、②、③、④中与是同类二次根式的是(　)

　　A．①和③　　B．②和③　　 C．①和④　　 D．③和④

  3．甲、乙两位同学对代数式 (a>0，b>0)，分别作了如下变形：

　　甲：

　　乙：

　　关于这两种变形过程的说法正确的是(　)

　　A．甲、乙都正确　　B．甲、乙都不正确　　C．只有甲正确　　  D．只有乙正确

  4．若ax²-5x+3=0是一元二次方程，则不等式3a+6>0的解集是(　)

　　A．a>-2　　 B．a<-2　　C．a>-2且a≠0　　D．a>

　5．等腰三角形、等边三角形、长方形、正方形和圆这五个图形中，是轴对称图形的个数是（　）

A．2　　 B．3　　 C．4　　  D．5

6．如右图所示的叙述正确的是(　)

　　A．由图形的绕其中心位置按同一方向连续旋转90°、180°、270°前后共四个图形所构成;

　　B．由图形的绕中心位置旋转45°、90°、135°、225°、270°、315°前后的图形共同组成的;

　　C．由图形的旋转100°所得;

　　D．绕该图形的中心旋转100°后所得图形还能与原图形重合.

  7．已知△ABC内接于⊙O，∠BOC=100°，则∠A=(　)

　　A．100°　　 B．50°　　 C．130°　　 D．50°或130°

　8．小明和三名女同学和四名男同学一起玩丢手帕游戏，小明随意将手帕丢在一名同学的后面，那么这名同学是女同学的概率是(　)

　　A．0　　  B．　　 C．

  9．小明任意买了一新电影票座位号是奇数的概率为(　)

　　A．0　　  B．　　 C．1　　 D．0到1之间

  10．若一扇形面积的数值恰好等于它弧长的数，则扇形的半径是(　)

　　A．1　　  B．2　　　C．3　　  D．4

二、填空题:

  1．计算的值是_______．

  2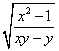．化成最简二次根式是________．

  3．化简 (-1<x<3)=________．

  4．已知一元二次方程ax²+x-b=0的一根为1，则a-b的值是______．

　5．已知一元二次方程ax²+bx+c=0(a≠0，b≠0)有一根是1，常数项为0，那么这个一元二次方程可写为_________(只写符合条件的一个即可)．

  6．把汉字“目”绕其中心旋转90°后，所得图形与汉字________相似．

  7．旋转不改变图形的_________和________．

　8．袋中装有一个红球和一个黄球，它们除了颜色外都相同，随机从中摸出一球，记录下颜色后放回袋中，充分摇匀后，再随机摸出一球，两次都摸到红球的概率是_____．

  9．过⊙O内一点M的最大弦长为10cm，最短弦长为8cm，那么OM的长是______．

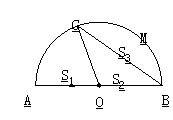　10．如右图所示，AB为半圆的直径，C为半圆上一点，

且为半圆的，设扇形AOC、△COB、弓形BMC的面

积分别为S₁、S₂、S₃，则S₁、S₂、S₃的大小关系式是______________________．

三、解答题:

1．化简：(1)  (1<a<8);　(2) .

2．解下列方程：

(1)-3x²+22x-24=0　　　　　　　　　　 (2)(3x+2)(x+3)=x+14

3．已知（-）²⁰⁰⁰·x=，求x的值．

4．已知x²-5x+1=0，求代数式的值．

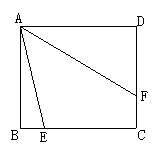
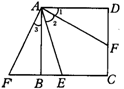
5．如右图所示，正方形ABCD的BC边上有一点E，∠DAE的平分线交CD于F，试用旋转的思想方法说明AE=DF+BE．

6．在掷骰子的游戏中，当两枚骰子的点数之和超过7时，小明点1分；当两枚骰子的点数之和不超过7时，小刚得1分，你认为该游戏对谁有利？

7．如右图所示，有一座拱桥圆弧形，它的跨度为60米，拱高为18米，当洪水泛滥到跨度只有30米时，就要采取紧急措施，若拱顶离水面只有4米，即PN=4米时，是否采取紧急措施？

8．建造一个长方形水池，原计划深3m，周长140m，经过研究觉得容量不够，于是长和宽都增加原计划的2倍，使容积达到14400m³，问新方案的长和宽各多少？

四、综合应用题．

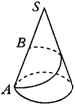
1．(开放题)如右图所示，已知圆锥底面半径r=10cm，母线长为40cm．

　　(1)求它的侧面展开图的圆心角和表面积．

(2)若一甲出从A点出发沿着圆锥侧面行到母线SA的中点B，请你动脑筋想一想它所走的最短路线是多少？为什么？

2．已知x是一元二次方程ax²+bx+c=0的根，求△=b²-4ac与M=(2ax₀+b)²的大小关系．

附加题:

　　求满足0<x<y及的不同整数对(x、y)的个数．

答案:

一、1．C　2．C　3．A　4．C　5．D　6．A　7．D　8．D　9．B　10．B

二、1．　3．4　4．-1　5．x²-x=0　6．

四　7．形状大小　8．  9．3cm　 10．S₂<S₁<S₃

三、1．(1)∵1<a<8，∴a-1>0，a-8<0，∴原式=8-a+1=9-a

　　(2)原式=(3-2--)÷=-×=-3

2．(1)3x²-22x+24=0，x₁=，x₂=6  (2)3x²+10x-8=0，x₁=，x₂=-4

3．x==-

4．原式=，

∵x²-5x+1=0，∴x²+1=5x，∴原式=5

5．如右图所示，将△ADF顺时针旋转90°，

则有∠3=∠1，∠AFD=∠F′，F′B=FD，

∵∠F′AE=∠3+∠BAE，∠AFD=∠FAB=∠2+∠BAE，

又∵∠1=∠2，

∴∠F′AE=∠F′，AE=EF′=BE+FD．

6．游戏对小刚有利　

7．不需要采取紧急措施　

8．长为80cm，宽为60cm

四、1．(1)90°  500　

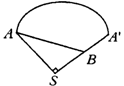
(2)如右图，这是一道开放题，由圆锥的侧面展开图可见，甲虫从A点出发沿着圆锥侧面绕行到母线SA的中点B所走的最短路线是线段AB的长，在Rt△ASB中，SA=40，SB=20，∴AB=20 (cm)，∴甲虫走的最短路线的长度是20http://www.1230.org/cm．

2．∵x₀是ax²+bx+c=0的根，

∴ax₀²+bx₀+c=0，ax₀²+bx₀=-c，

M=(2ax₀+b)²=4a²x₀²+4ax₀b+b²=4a(ax₀²+bx₀)+b²=-4ac+b²=b²-4ac=△，

∴M与△的大小关系为M=△．

附加题：

∵1088=8²×17，∴8=，

由此可知，x必具有17t²的形式，y必具有17k²形式，且t+k=8(t，k均为正整数)，

∵0<x<y，∴t<k．

当t=1，k=7时，(x，y)=(17，833)，

当t=2，k=6时，(x，y)=(68，612)．

当t=3，k=5时，(x，y)=(153，425)，

∴不同的整数对的个数为3．