概率与统计中考题
1.(2006年浙江省绍兴市) 一个不透明的袋中装有除颜色外其余均相同的5个红球和3个黄球,从中随机摸出一个,则摸到黄球的概率是( )
A.1/8 B.1/3 C.3/8 D.3/5
2.(2006年重庆市。课改)现有A、B两枚均匀的小立方体(立方体的每个面上分别标有数字1,2,3,4,5,6).用小莉掷A立方体朝上的数字为![]() 、小明掷B立方体朝上的数字为
、小明掷B立方体朝上的数字为![]() 来确定点P(
来确定点P(![]() ),那么它们各掷一次所确定的点P落在已知抛物线
),那么它们各掷一次所确定的点P落在已知抛物线![]() 上的概率为( )
上的概率为( )
A. ![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.(2006年大连市)一鞋店试销一种新款女鞋,试销期间卖出情况如下表:
| 型号 | 22 | 22.5 | 23 | 23.5 | 24 | 24.5 | 25 |
| 数量(双) | 3 | 5 | 10 | 15 | 8 | 3 | 2 |
对于这个鞋店的经理来说最关心哪种型号鞋畅销,则下列统计量对鞋店经理来说最有意义的是( )
A、平均数 B、众数 C、中位数 D、标准差
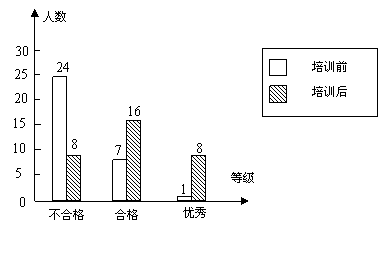
4.(2006年大连市)某校320名学生在电脑培训前后各参加了一次水平相同的考试,考分都以同一标准划分成“不合格”、“合格”、“优秀”三个等级,为了了解电脑培训的效果,随机抽取32名学生两次考试考分等级的统计图(如图8),试回答下列问题:
(1)这32名学生经过培训,考分等级“不及格”的百分比由______下降到__________;
(2)估计该校320名学生,培训后考分等级为“合格”与“优秀”的学生共有____名;
(3)你认为上述估计合理吗?理由是什么?
答:____________________。理由:__________________________。
 |
5.(2006年大连市)在围棋盒中有x颗黑色棋子和y颗白色棋子,从盒中随机地取出一个棋子,如果它是黑色棋子的概率是![]() 。
。
(1)试写出y与x的函数关系式。www.1230.org 初中数学资源网
(2)若往盒中再放进10颗黑色棋子,则取得黑色棋子的概率变为![]() ,求x和y的值。
,求x和y的值。
6.(江西省)一次期中考试中,A、B、C、D、E五位同学的数学、英语成绩等有关信息如下表所示:(单位:分)
| A | B | C | D | E | 平均分 | 标准差 | |
| 数学 | 71 | 72 | 69 | 68 | 70 |
| |
| 英语 | 88 | 82 | 94 | 85 | 76 | 85 |
(1)求这五位同学在本次考试中数学成绩的平均分和英语成绩的标准差;
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式是:标准分=(个人成绩-平均成绩)÷成绩标准差。
从标准分看,标准分大的考试成绩更好。请问A同学在本次考试中,数学与英语哪个学科考得更好?
友情提示:一组数据的标准差计算公式是S=![]() ,其中
,其中![]() 为n个数据
为n个数据![]() 、
、![]() …
…![]() r的平均数。
r的平均数。
7.(2006年长春市)某商场家电部为了调动营业员的工作积极性,决定实行目标等级管理。商场家电部统计了每人营业员在某月的销售额,数据如下:(单位:万元)
23 17 16 20 32 30 16 15 15 26
15 32 23 17 15 15 28 28 16 21
(1)这组数据的众数为_________________万元;中位数为_________________万元。(2分)
 (2)商场规定月销售额达到或超过25万元为A级,低于19万元为C级,其他为B级,为了使商场负责人对各等级人数比例情况一目了然,请作出扇形统计图。(4分)
(2)商场规定月销售额达到或超过25万元为A级,低于19万元为C级,其他为B级,为了使商场负责人对各等级人数比例情况一目了然,请作出扇形统计图。(4分)
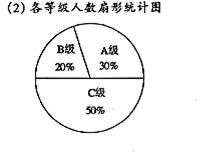
(1)众数为15万元;中位数为18.5万元。
 8.(2006年长春市)若一组数据1,2,3,x的极差为6,则x的值是D
8.(2006年长春市)若一组数据1,2,3,x的极差为6,则x的值是D
A.7 B.8 C.9 D.7或-3
9.(2006年长春市)晓明玩转盘游戏,当他转动如图所示的转盘,转盘停止时指针指向2的概率是_____。![]()
10.(2006年长春市)袋中共有5个大小相同的红球、白球,任意摸出一球为红球的概率是![]() 。
。
(1)袋中红球、白球各有几个?(2)任意摸出两个球均为红球的概率是________________。(1)![]() 答:袋中有2个红球,3个白球。(2)
答:袋中有2个红球,3个白球。(2)![]()
11.(2006年海淀区)某班主任老师想了解本班学生平均每月有多少零用钱,随机抽取了10名同学进行调查,他们每月的零用钱数目是(单位:元)10,20,20,30,20,30,10,10,50,100,则该班学生每月平均零用钱约为( ) C
A. 10元 B. 20元 C. 30元 D. 40元
12.(2006年海淀区)四张扑克牌的牌面如图①所示,将扑克牌洗均匀后,如图②背面朝上放置在桌面上。
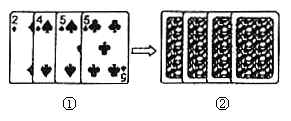
(1)若随机抽取一张扑克牌,则牌面数字恰好为5的概率是_____________;
(2)规定游戏规则如下:若同时随机抽取两张扑克牌,抽到两张牌的牌面数字之和是偶数为胜;反之,则为负。你认为这个游戏是否公平?请说明理由。
解:(1)![]() ; (2)不公平。
; (2)不公平。
画树状图如图所示:
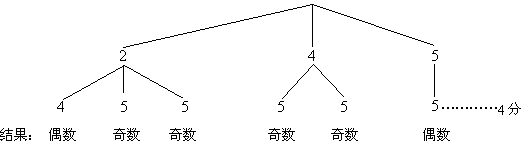
(其它方法相应给分)
所以P(和为偶数)=![]() ,P(和为奇数)=
,P(和为奇数)=![]()
因为P(和为偶数)≠P(和为奇数),所以游戏不公平。
13.(2006年旅顺口区)数学老师对小明参加的4次中考数学模拟考试成绩进行统计分析,判断小明的数学成绩是否稳定,于是老师需要知道小明这4次数学成绩的 ( ) D
A、平均数 B、众数 C、中位数 D、标准差
14.(2006年旅顺口区)在“石头、剪子、布”的游戏中,两人做同样手势的概率是 . ![]() ;
;
15.(2006年旅顺口区)某区从2300名参加初中毕业升学统一考试数学试测的学生
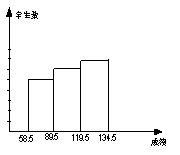 中随机抽取200名学生的试卷,成绩从低到高按59~89、90
中随机抽取200名学生的试卷,成绩从低到高按59~89、90
~119、120~134、135~150分成四组进行统计(最低成绩
为59分,且分数均为整数),整理后绘出如图所示的各分数
段频数分布直方图的一部分.已知前三个小组从左到右的频
率依次为0.25、0.30、0.35.
⑴第四组的频数为 ,并将频数分布直方图补充
完整;
⑵若90分及其以上成绩为及格,则此次测试中数学成绩及格以上(含及格)的人数约为 .
解:(1)20;图略;(2)1725.
16.(2006年贵阳市)桌面上放有4张卡片,正面分别标有数字1,2,3,4,这些卡片除数字外完全相同,把这些卡片反面朝上洗匀后放在桌面上,甲从中任意抽出一张,记下卡片上的数字后仍放反面朝上放回洗匀,乙从中任意抽出一张,记下卡片上的数字,然后将这两数相加;
(1)请用列表或画树状图的方法求两数和为5的概率;(6分)
(2)若甲与乙按上述方式作游戏,当两数之和为5时,甲胜;反之则乙胜;若甲胜一次得12分,那么乙胜一次得多少分,这个游戏对双方公平吗?
| 1 | 2 | 3 | 4 | |
| 1 | (1,1) | (1,2) | (1,3) | (1,4) |
| 2 | (2,1) | (2,2) | (2,3) | (2,4) |
| 3 | (3,1) | (3,2) | (3,3) | (3,4) |
| 4 | (4,1) | (4,2) | (4,3) | (4,4) |
(1)列表如下:
由列表可得:P(数字之和为5)=![]() ;(2)因为P(甲胜)=
;(2)因为P(甲胜)=![]() ,P(乙胜)=
,P(乙胜)=![]() ,∴甲胜一次得12分,要使这个游戏对双方公平,乙胜一次得分应为:
,∴甲胜一次得12分,要使这个游戏对双方公平,乙胜一次得分应为:![]() (分)
(分)
17.(2006年贵阳市)贵阳市某中学开展以“八荣八耻”为主题的社会主义荣辱观教育活动,举办了演讲、书法、作文、手抄报、小品、漫画六项比赛(每个同学限报一项),学生参赛情况如下表:
| 比赛项目 | 演讲 | 书法 | 作文 | 手抄报 | 小品 | 漫画 |
| 参赛人数(人) | 36 | 90 | 60 | 15 | ||
| 比例(%) | 12 | 25 | 20 | 8 | 5 |
认真阅读统计表后,回答下列问题:
(1)请补充完成这统计表;(3分)
(2)本次参加比赛的总人数是 人,本次比赛项目的“众数”是 ;(4分)
(3)手抄报作品与漫画作品的获奖人数分别是6人和3人,你认为“手抄报作品比漫画作品的获奖率高”这种说法否正确,请说明你的理由;(3分)
(1)75,30,24 ;(2)300, 作文 ;(3)不正确。因为手抄报作品的获奖率为10%,漫画作品的获奖率为20%。
18.(2006年贵阳市)在一节综合实践课上,六名同学做手工的数量(单位:件)分别是:5,7,3,6,6,4;则这组数据的中位数为 件;5.5
19.(2006年贵阳市)掷一枚质地均匀的小正方体,它的六个面上分别
标有1、2、3、4、5、6,则朝上一面的数字是奇数的概率是 ;![]()
20.(2006年贵阳市)以下适合普查的是 ( )C
(A)了解一批灯泡的使用寿命 (B)调查全国八年级学生的视力情况
(C)评价一个班级升学考试的成绩 (D)了解贵州省的家庭人均收入
21.(2006年南安市)甲、乙两人在某公司做见习推销员,推销“小天鹅”洗衣机,他们在1~8月份的销售情况如下表所示:
| 月份 | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 | 7月 | 8月 |
| 甲的销售量(单位:台) | 7 | 8 | 6 | 7 | 6 | 6 | 7 | 7 |
| 乙的销售量(单位:台) | 5 | 6 | 5 | 6 |
| 7 | 8 | 9 |
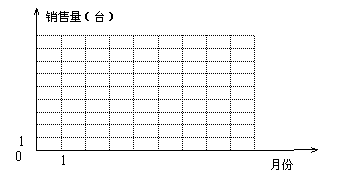
(1)在右边给出的坐标系中,绘制甲乙两人这8个月的月销售量的
折线图(甲用实线;乙用虚线);
(2) 根据(1)中的折线图,写出2条关于
甲乙两人在这8个月中的销售状况的信息:
① ;
② .
⑴ 图略,每画对甲、乙的一条折线得2分.⑵每写对(大意正确者)一条信息得2分。
(2006年南安市)小明和小亮玩一个游戏:三张大小、质地都相同的卡片上分别标有数字1,2,3,现将标有数字的一面朝下. 小明从中任意抽取一张,记下数字后放回洗匀,然后小亮从中任意抽取一张.,计算小明和小亮抽得的两个数字之和,如果和为奇数则小明胜,和为偶数则小亮胜.
⑴ 用列表或画树状图等方法,列出小明和小亮抽得的数字之和所有可能出现的情况;
⑵请判断该游戏对双方是否公平,并说明理由.
解:⑴(法一)列表如下:
|
| 1 | 2 | 3 | ||||||||||||
| 1 | 1+1=2 | 2+1=3 | 3+1=4 | ||||||||||||
| 2 | 1+2=3 | 2+2=4 | 3+2=5 | ||||||||||||
| 3 | 1+3=4 | 2+3=5 | 3+3=6 |
由上表可知,所有等可能的结果共有9种,(法二)画树状图略。
⑵∵P(和为奇数)=![]() ,P(和为偶数)=
,P(和为偶数)=![]() ,∴这个游戏规则对双方是不公平的.
,∴这个游戏规则对双方是不公平的.
22.(2006年泰州市)下列说法正确的是B
A.为了了解我市今年夏季冷饮市场冰淇淋的质量可采用普查的调查方式进行.
B.为了了解一本300页的书稿的错别字的个数,应采用普查的调查方式进行.
C.销售某种品牌的鞋,销售商最感兴趣的是所销售的鞋的尺码的平均数.
D.为了了解我市九年级学生中考数学成绩,从所有考生的试卷中抽取1000份试卷进行统计分析,在这个问题中,样本是被抽取的1000名学生.
23.(2006年泰州市)投掷一枚普通的正方体骰子,四位同学各自发表了以下见解:B
①出现“点数为奇数”的概率等于出现“点数为偶数”的概率.
②只要连掷6次,一定会“出现一点”.
③投掷前默念几次“出现6点”,投掷结果“出现6点”的可能性就会加大.
④连续投掷3次,出现的点数之和不可能等于19.
其中正确的见解有
A.1个 B.2个 C.3个 D.4个
24.
(2006年南安市)0的绝对值是 . 0;
(2006年南安市)当x_______________时,分式![]() 没有意义.=1;
没有意义.=1;
(2006年南安市)某种感冒病毒的直径是0.米,用科学记数法表示为_____________ 米.1.2×10![]() ;
;
(2006年南安市)一射击运动员在一次射击练习中打出的成绩是(单位:环):7,8,9,8,6,8,10,7,这组数据的众数是_________环.8;
(2006年南安市)不等式2x-1>5的解集为 .x>3;
(2006年南安市)方程组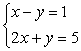 的解是____________.
的解是____________.
(2006年南安市)已知等腰梯形的一个内角为100°,则其余三个角的度数分别是 .100、80、80;
(2006年南安市)试写出图象位于第二、四象限的一个反比例函数的解析式
.开放题,例如y= -![]() 等;
等;
 (2006年南安市)如果一个多边形的内角和等于外角和的2倍,那么这个多边形的边数n= .
(2006年南安市)如果一个多边形的内角和等于外角和的2倍,那么这个多边形的边数n= .
(2006年南安市)在体育达标跳绳项目测试中,1分钟跳160次为达标,小敏记录了他预测时1分钟跳的次数分别为145, 155, 140, 162, 164. 则他在该预测中达标的概率是__________.![]()
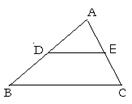
(2006年南安市)如图,DE是△ABC的中位线,S△ADE = 2,则S△ABC= . 8;
(2006年南安市)观察分析下列数据,寻找规律: 0,![]() ,
,![]() ,3,2
,3,2![]() ,
,![]() ,3
,3![]() ,……,
,……,
|
(2006年南安市)下列运算正确的是( )C;
A. x2+x2=x4 ; B.(a-1)2=a2-1 ; C.a2·a3=a5 ; D.3x+2y=5xy .
(2006年南安市)已知⊙![]() 和⊙
和⊙![]() 的半径分别为2cm和3cm,两圆的圆心距是1cm,则两圆的位置关系是( ) D;
的半径分别为2cm和3cm,两圆的圆心距是1cm,则两圆的位置关系是( ) D;
A.外离; B.外切; C.相交; D.内切.
(2006年南安市)下列调查方式,你认为正确的是 ( ) B;
A. 了解一批炮弹的杀伤半径,采用普查方式;
B. 了解南安市每天的流动人口数,采用抽查方式;
C. 要保证“神舟6号”载人飞船成功发射,对重要零部件采用抽查方式检查;
D. 了解南安市居民日平均用水量,采用普查方式.
(2006年南安市)下列事件中,属于随机事件的是( )B;
A.掷一枚普通正六面体骰子所得点数不超过6 ; B.买一张体育彩票中奖;
C.太阳从西边落下;
D.口袋中装有![]() 个红球,从中摸出一个白球.
个红球,从中摸出一个白球.
(2006年泰州市)小明和小兵两人参加学校组织的理化实验操作测试,近期的5次测试成绩如右图所示,则小明5次成绩的方差S12与小兵5次成绩的方差S22之间的大小关系为S12
S22.(填“>”、“<”、“=”)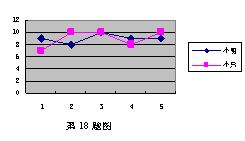

(2006年泰州市) 为了配合“八荣八耻”宣传教育,针对闯红灯的现象时有发生的实际情况,八年级某班开展一次题为“红灯与绿灯”的课题学习活动,它们将全班学生分成8个小组,其中第①~⑥组分别负责早、中、晚三个时段闯红灯违章现象的调查,第⑦小组负责查阅有关红绿灯的交通法规,第⑧小组负责收集有关的交通标志. 数据汇总如下:
| 时间 | 负责组别 | 车流总量 | 每分钟车流量 |
| 早晨上学6:30~7:00 | ①② | 2747 | 92 |
| 中午放学11:20~11:50 | ③④ | 1449 | 48 |
| 下午放学5:00~5:30 | ⑤⑥ | 3669 | 122 |
部分时段车流量情况调查表
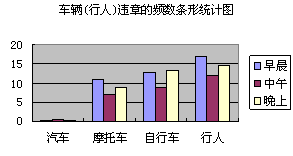
回答下列问题:
⑴请你写出2条交通法规:① .
② .
⑵画出2枚交通标志并说明标志的含义.


标志含义: 标志含义:
⑶早晨、中午、晚上三个时段每分钟车流量的极差是 ,这三个时段的车流总量的中位数是 .
⑷观察表中的数据及条形统计图,写出你发现的一个现象并分析其产生的原因.
⑸通过分析写一条合理化建议.
(2006年泰州市)三人相互传球,由甲开始发球,并作为第一次传球.
⑴用列表或画树状图的方法求经过3次传球后,球仍回到甲手中的概率是多少?
⑵由⑴进一步探索:经过4次传球后,球仍回到甲手中的不同传球的方法共有多少种?
⑶就传球次数![]() 与球分别回到甲、乙、丙手中的可能性大小,提出你的猜想(写出结论即可).
与球分别回到甲、乙、丙手中的可能性大小,提出你的猜想(写出结论即可).
(2006年苏州市)某校测量了初三(1)班学生的身高(精确到1cm),
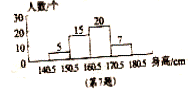 按10cm为一段进行分组,得到如下频数分布直方图,则下列说法正确的是 ( )D
按10cm为一段进行分组,得到如下频数分布直方图,则下列说法正确的是 ( )D
A.该班人数最多的身高段的学生数为7人 B.该班身高低于160.5cm的学生数为15人
C.该班身高最高段的学生数为20人 D.该班身高最高段的学生数为7人
(2006年苏州市)下列说法正确的是 ( )D
A.一颗质地均匀的骰子已连续抛掷了2000次,其中,抛掷出5点的次数最少,则第2001
次一定抛掷出5点
B.某种彩票中奖的概率是1%,因此买100张该种彩票一定会中奖
C.天气预报说明天下雨的概率是50%.所以明天将有一半时间在下雨
D.抛掷一枚图钉,钉尖触地和钉尖朝上的概率不相等
(2006年苏州市)某校参加“姑苏晚报·可口可乐杯”中学生足球赛的队员的年龄如下(单位:岁):13,14,16,15,14,15,15,15,16,14,则这些队员年龄的众数是_____.15;
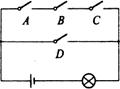 (2006年苏州市)如图.电路图上有四个开关A、B、C、D和一个小灯泡,闭合开关D或同时闭合开关A,B,C都可使小灯泡发光。
(2006年苏州市)如图.电路图上有四个开关A、B、C、D和一个小灯泡,闭合开关D或同时闭合开关A,B,C都可使小灯泡发光。
(1)任意闭合其中一个开关,则小灯泡发光的概率等于___;
(2)任意闭合其中两个开关,请用画树状图或列表的方法求出小
灯泡发光的概率.
(1)![]() .
(2)正确画出树状图(或列表)
.
(2)正确画出树状图(或列表) 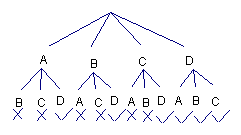
第1个开关
第2个开关
结果 任意闭合其中两个开关的情况共有12种,其中能使小灯泡发光的情况有6种
小灯泡发光的概率是![]()
(2006年苏州市)今年,苏州市政府的一项实事工程就是由政府投人1 000万元资金.对城区4万户家庭的老式水龙头和13升抽水马桶进行免费改造.某社区为配合政府完成该项工作,对社区内1200户家庭中的120户进行了随机抽样调查,并汇总成下表:
| 改造 情况 | 均不 改造 | 改造水龙头 | 改造马桶 | ||||
| 1个 | 2个 | 3个 | 4个 | 1个 | 2个 | ||
| 户数 | 20 | 31 | 28 | 21 | 12 | 69 | 2 |
(1)试估计该社区需要对水龙头、马桶进行改造的家庭共有_____户;
(2)改造后.一只水龙头一年大约可节省5吨水,一只马桶一年大约可节省15吨水.试估
计该社区一年共可节约多少吨自来水?
(3)在抽样的120户家庭中.既要改造水龙头又要改造马桶的家庭共有多少户?
(1)1000;(2)抽样的120户家庭一年共可节约用水:(1×31+2×28+×21+4×12)× 5+(1×69+2×2)×15=198×5+73×15=2085。2085×![]() =20850(吨)。答:该社区一年共可节约用水20850吨。(3)设既要改造水龙头又要改造马桶的家庭共有x户,则只改造水龙头不改造马桶的家庭共有(92一x)户,只改造马桶不改造水龙头的家庭共有(71一x)户,
∴ x+(92一x)+(71一x)=100,∴x=63(户)。答:既要改造水龙头又要改造马桶的家庭共有63户.
=20850(吨)。答:该社区一年共可节约用水20850吨。(3)设既要改造水龙头又要改造马桶的家庭共有x户,则只改造水龙头不改造马桶的家庭共有(92一x)户,只改造马桶不改造水龙头的家庭共有(71一x)户,
∴ x+(92一x)+(71一x)=100,∴x=63(户)。答:既要改造水龙头又要改造马桶的家庭共有63户.
例6.(06年四川省乐山市)下表是某市2001年到2005年第一、第二、第三产业产值的统计情况.
| 年 份 | 2001年 | 2002年 | 2003年 | 2004年 | 2005年 |
| 第一产业产值(亿元) |
|
|
|
|
|
| 第二产业产值(亿元) |
|
|
|
|
|
| 第三产业产值(亿元) |
|
|
|
|
|
(1)2005年该市第一、第二、第三产业产值总和达到_________亿元,其中第一产业的产值占总和的_________![]() ;
;
(2)该市2005年第二产业的产值在2004年的基础上下降了_________![]() ,2005年第三产业的产值是
,2005年第三产业的产值是![]() 年第三产业的产值的_________倍;
年第三产业的产值的_________倍;
(3)下图已画出该市2001年到2005年的第一、第三产业产值的折线图,请你在图中画出第二产业产值的折线图.
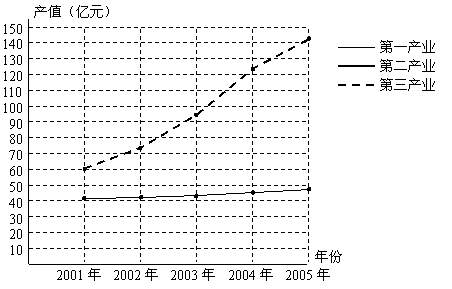
(4)从折线图可以看出该市第一、第二、第三产业的发展特点,请写出两条.
①_____________________________________________________________________________
______________________________________________________________________________;
②_____________________________________________________________________________
______________________________________________________________________________;
 7
7