函数中考题选
1.(2006年浙江省绍兴市)小敏在某次投篮中,球的运动路线是抛物线![]() 的一部分(如图),若命中篮圈中心,则他与篮底的距离l是
的一部分(如图),若命中篮圈中心,则他与篮底的距离l是
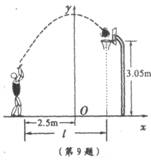 A.3.5m
A.3.5m
B.4m
C.4.5m
D.4.6m
2.(2006年浙江省绍兴市)如图,正方形OABC,ADEF的顶点A,D,C在坐标轴上,点F在AB上,点B,E在函数![]() 的图象上,则点E的坐标是
的图象上,则点E的坐标是
 A.
A.![]()
B.![]()
C.![]()
D.![]()
3.(2006年浙江省绍兴市)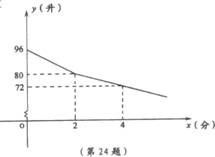 某校部分住校生,放学后到学校锅炉房打水,每人接水2升,他们先同时打开两个放水笼头,后来因故障关闭一个放水笼头.假设前后两人接水间隔时间忽略不计,且不发生泼洒,锅炉内的余水量y(升)与接水时间x(分)的函数图象如图.
某校部分住校生,放学后到学校锅炉房打水,每人接水2升,他们先同时打开两个放水笼头,后来因故障关闭一个放水笼头.假设前后两人接水间隔时间忽略不计,且不发生泼洒,锅炉内的余水量y(升)与接水时间x(分)的函数图象如图.
请结合图象,回答下列问题:
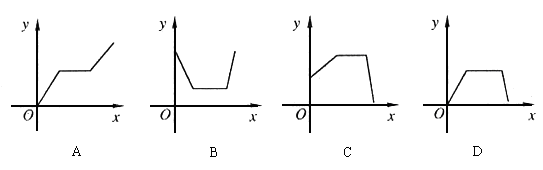
(1)根据图中信息,请你写出一个结论;
(2)问前15位同学接水结束共需要几分钟?
(3)小敏说:“今天我们寝室的8位同学去锅炉房连续接完水恰好用了3分钟.”你说可能吗?请说明理由.
 4.(2006年重庆市)观察市统计局公布的“十五”时期重庆市农村居民人均 收入每年比上一年增长率的统计图,下列说法正确的是( )
4.(2006年重庆市)观察市统计局公布的“十五”时期重庆市农村居民人均 收入每年比上一年增长率的统计图,下列说法正确的是( )
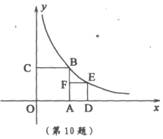
A.2003年农村居民人均收入低于2002年
B.农村居民人均收入比上年增长率低于9%的有2年
C.农村居民人均收入最多时2004年
D.农村居民人均收入每年比上一年的增 长率有大有小,但农村居民人均收入在持续增加
5.(2006年大连市)在平面直角坐标系中,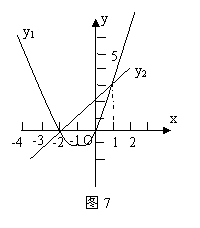 点P(-2,3)在 (
)
点P(-2,3)在 (
)
A、第一象限 B、第二象限 C、第三象限 D、第四象限
6.(2006年大连市)如图7是二次函数y1=ax2+bx+c和一次函数y2=mx+n的图象,观察图象写出y2≥y1时,x的取值范围______________。
7.(2006年大连市)如图11,直线y=k和双曲线![]() 相交于点P,过P点作PA0垂直x轴,垂足为A0,x轴上的点A0、A1、A2、…A n 的横坐标是连续的整数,过点A1、A2、…A n分别作x轴的垂线,与双曲线
相交于点P,过P点作PA0垂直x轴,垂足为A0,x轴上的点A0、A1、A2、…A n 的横坐标是连续的整数,过点A1、A2、…A n分别作x轴的垂线,与双曲线![]() (x>0)及直线y=k分别交于点B1、B2、…B n ,C1、C2、…C n 。(1)求A0点坐标;(2)求
(x>0)及直线y=k分别交于点B1、B2、…B n ,C1、C2、…C n 。(1)求A0点坐标;(2)求![]() 及
及![]() 的值;
的值;
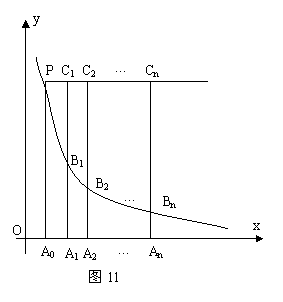
 (3)试猜想
(3)试猜想![]() 的值(直接写答案)
的值(直接写答案)
8.(江西省)一条抛物线y=![]() 经过点(0,
经过点(0,![]()
(1)求这条抛物线的解析式,并写出它的顶点坐标坐标;
(2)现有一半径为1,圆心P在抛物线上运动的动圆,当⊙P与坐标轴相切时,求轴心P的坐标。
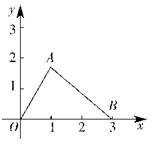
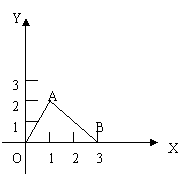 9.(江西省)如图,在平面直角坐标系中,点A在第一象限,点B的坐标为(3,0),OA=2,∠AOB=60º。(1)求点A的坐标;(2)若直线AB交y轴于点C,求△AOC的面积。
9.(江西省)如图,在平面直角坐标系中,点A在第一象限,点B的坐标为(3,0),OA=2,∠AOB=60º。(1)求点A的坐标;(2)若直线AB交y轴于点C,求△AOC的面积。
10.(江西省)近视眼镜的度数y(度)与镜片焦距x(m)成反比例,已知400度的近视眼镜镜片的焦距为0.25m,则y与x的函数关系式为__________________。
11.(2006年长春市)如图,在平面直角坐标系中,两个函数![]() 的图象交于点A。动点P从点O开始沿OA方向以每秒1个单位的速度运动,作PQ∥x轴交直线BC于点Q,以PQ为一边向下作正方形PQMN,设它与△OAB重叠部分的面积为S。
的图象交于点A。动点P从点O开始沿OA方向以每秒1个单位的速度运动,作PQ∥x轴交直线BC于点Q,以PQ为一边向下作正方形PQMN,设它与△OAB重叠部分的面积为S。
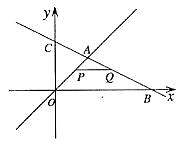 (1)求点A的坐标。(2分)
(1)求点A的坐标。(2分)
(2)试求出点P在线段OA上运动时,S与运动时间t(秒)的关系式。(4分)
(3)在(2)的条件下,S是否有最大值?若有,求出t为何值时,S有最大值,并求出最大值;若没有,请说明理由。(2分)
(4分)若点P经过点A后继续按原方向、原速度运动,当正方形PQMN与△OAB重叠部分面积最大时,运动时间t满足的条件是____________。(2分)
解:(1)由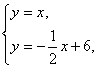 可得
可得![]() ∴A(4,4)。
∴A(4,4)。
(2)点P在y = x上,OP
= t,则点P坐标为![]() 点Q的纵坐标为
点Q的纵坐标为![]() ,并且点Q在
,并且点Q在![]() 上。∴
上。∴![]() ,即点Q坐标为
,即点Q坐标为![]() 。
。![]() 。当
。当![]() 时,
时,![]() 。当
。当![]() ,
, ![]() 当点P到达A点时,
当点P到达A点时,![]() ,当
,当![]() 时,
时, ![]()
![]() 。(3)有最大值,最大值应在
。(3)有最大值,最大值应在![]() 中,
中, ![]() 当
当![]() 时,S的最大值为12。(4)
时,S的最大值为12。(4)![]() 。
。
12.(2006年长春市)某厂生产一种零件,每个成本为40元,销售单价为60元。该厂为了鼓励客户购买,决定当一次购买零件超过100个时,多购买一个,全部零件的销售单价均降低0.02元,但不能低于51元。
(1)当一次购买多少个零件时,销售单价恰为51元?(3分)
(2)设一次购买零件x个时,销售单价为y元,求y与x的函数关系式。(4分)
(3)当客户一次购买500个零件时,该厂获得的利润是多少?当客户一次购买1000个零碎件时,利润又是多少?(利润 = 售价-成本)(3分)
解:(1)设当一次购买x个零件时,销售单价为51元,则
(x-100)×0.02 = 60-51,
解得 x = 550。
答:当一次购买550个零件时,销售单价为51元。 (3分)
(2)当0<x≤100时, y = 60;
当100<x≤550时, y = 62-0.02x;
当x>550时, y = 51。 (7分)
(3)当x = 500时,利润为
(62-0.02×500)×500-40×500 = 6000(元)。
当x = 1000时,利润为1000×(51-40)= 11000(元)。
答:当一次购买500个零件时,该厂获得利润为6000元;当一次购买1000个零件时,该厂获得利润11000元。
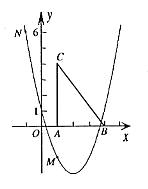 13.(2006年长春市)如图,二资助函数
13.(2006年长春市)如图,二资助函数![]() 的图象经过点M(1,—2)、N(—1,6)。
的图象经过点M(1,—2)、N(—1,6)。
(1)求二次函数![]() 的关系式。(3分)
的关系式。(3分)
(2)把Rt△ABC放在坐标系内,其中∠CAB = 90°,点A、B的坐标分别为(1,0)、(4,0),BC = 5。将△ABC沿x轴向右平移,当点C落在抛物线上时,求△ABC平移的距离。(4分)
解:(1)∵M(1,-2),N(-1,6)在二次函数y = x2+bx+c的图象上,
∴![]() 解得
解得![]() 二次函数的关系式为y = x2-4x+1。
二次函数的关系式为y = x2-4x+1。
(2)Rt△ABC中,AB = 3,BC = 5,∴AC = 4,![]()
 解得
解得![]() ∵A(1,0),∴点C落在抛物线上时,△ABC向右平移
∵A(1,0),∴点C落在抛物线上时,△ABC向右平移![]() 个单位。
个单位。
14.(2006年长春市)甲、乙两个水桶内水面的高度y(cm)与放水(或注水)的时间x(分)之间的函数图象如图所示,当两个水桶内水面高度相同时,x约为____________分。(精确到0.1分) 2.7(2.6、2.8亦可)
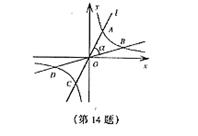 15.(2006年长春市)如图,直线l与双曲线交于A、C两点,将直线l绕点O顺时针旋转
15.(2006年长春市)如图,直线l与双曲线交于A、C两点,将直线l绕点O顺时针旋转![]() 度角(0°<
度角(0°<![]() ≤45°),与双曲线交于B、D两点,则四边形ABCD的形状一定是_________形。平行四边(形)
≤45°),与双曲线交于B、D两点,则四边形ABCD的形状一定是_________形。平行四边(形)
16.(2006年长春市)用铝合金型材做一个形状如图1所示的矩形窗框,设窗框的一边为xm,窗户的透光面积为ym2,y与x的函数图象如图2所示。
(1)观察图象,当x为何值时,窗户透光面积最大?(3分)
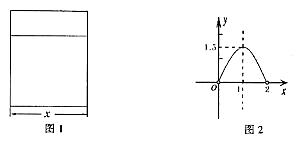 (2)当窗户透光面积最大时,窗框的另一边长是多少?(2分)
(2)当窗户透光面积最大时,窗框的另一边长是多少?(2分)
解:(1)由图象可知,当x = 1时,窗户透光面积最大。(2)窗框另一边长为1.5米。
17.(2006年海淀区)在函数![]() 中,自变量x的取值范围是( )A
中,自变量x的取值范围是( )A
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
18.(2006年海淀区)打开某洗衣机开关,在洗涤衣服时(洗衣机内无水),洗衣机经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间满足某种函数关系,其函数图象大致为( )D
19.(2006年海淀区)二次函数![]() 的最小值是_____________。 2
的最小值是_____________。 2
20.(2006年海淀区)已知抛物线![]() 的部分图象如图1所示。
的部分图象如图1所示。
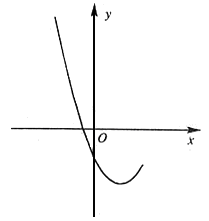
图1 图2
(1)求c的取值范围;
(2)若抛物线经过点(0,-1),试确定抛物线![]() 的解析式;
的解析式;
(3)若反比例函数![]() 的图象经过(2)中抛物线上点(1,a),试在图2所示直角坐标系中,画出该反比例函数及(2)中抛物线的图象,并利用图象比较
的图象经过(2)中抛物线上点(1,a),试在图2所示直角坐标系中,画出该反比例函数及(2)中抛物线的图象,并利用图象比较![]() 与
与![]() 的大小。
的大小。
解:(1)根据图象可知![]() ,且抛物线
,且抛物线![]() 与x轴有两个交点, 所以一元二次方程
与x轴有两个交点, 所以一元二次方程![]() 有两个不等的实数根。所以
有两个不等的实数根。所以![]() ,且
,且![]() , 所以
, 所以![]() ;
;
(2)因为抛物线经过点(0,-1), 把![]() 代入
代入![]()
得![]() ,故所求抛物线的解析式为
,故所求抛物线的解析式为![]() ;
;
(3)因为反比例函数![]() 的图象经过抛物线
的图象经过抛物线![]() 上的点(1,a), 把
上的点(1,a), 把![]() 代入
代入![]() ,得
,得![]() , 把
, 把![]() 代入
代入![]() ,得
,得![]() ,所以
,所以![]() 。 画出
。 画出![]() 的图象如图所示。
的图象如图所示。
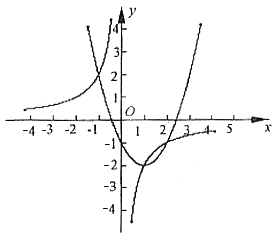
观察图象,![]() 除交点(1,-2)外,还有两个交点大致为
除交点(1,-2)外,还有两个交点大致为![]() 和
和![]()
把![]() 和
和![]() 分别代入
分别代入![]() 和
和![]() 可知,
可知,
![]() 和
和![]() 是
是![]() 的两个交点。 根据图象可知:当
的两个交点。 根据图象可知:当![]() 或
或![]() 或
或![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() 。
。
21.(2006年海淀区)如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C。
(1)用直尺画出该圆弧所在圆的圆心M的位置;
(2)若A点的坐标为(0,4),D点的坐标为(7,0),试验证点D是否在经过点A、B、C的抛物线上;
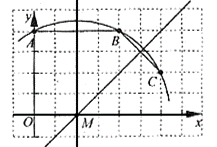 (3)在(2)的条件下,求证直线CD是⊙M的切线。
(3)在(2)的条件下,求证直线CD是⊙M的切线。
解:(1)如图1,点M即为所求。
(2)由A(0,4),可得小正方形的边长为1,从而B(4,4)、C(6,2)。 设经过点A、B、C的抛物线的解析式为![]() , 依题意
, 依题意![]() ,解得
,解得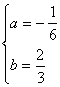 , 所以经过点A、B、C的抛物线的解析式为
, 所以经过点A、B、C的抛物线的解析式为![]() , 把点D(7,0)的横坐标
, 把点D(7,0)的横坐标![]() 代入上述解析式,得:
代入上述解析式,得: ![]() ,所以点D不在经过A、B、C的抛物线上。
,所以点D不在经过A、B、C的抛物线上。
(3)如图2,设过C点与x轴垂直的直线与x轴的交点为E,连结MC,作直线CD。
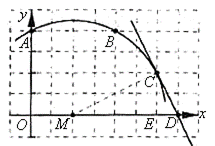
图2
所以CE=2,ME=4,ED=1,MD=5, 在Rt△CEM中,∠CEM=90°, 所以![]() , 在Rt△CED中,∠CED=90°,所以
, 在Rt△CED中,∠CED=90°,所以![]() ,所以
,所以![]() , 所以∠MCE=90°, 因为MC为半径, 所以直线CD是⊙M的切线。
, 所以∠MCE=90°, 因为MC为半径, 所以直线CD是⊙M的切线。
22.(2006年旅顺口区)在平面直角坐标系中,点P(3, -2)在 ( )D
A、第一象限 B、第二象限 C、第三象限 D、第四象限
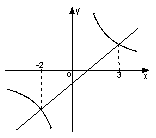 23.(2006年旅顺口区)如图是一次函数y1=kx+b和反比例函数y2=
23.(2006年旅顺口区)如图是一次函数y1=kx+b和反比例函数y2=![]() 的图象,观察图象写出y1>y2时,
的图象,观察图象写出y1>y2时,![]() 的取值范围 .-2<x<0或x>3.
的取值范围 .-2<x<0或x>3.
24.(2006年旅顺口区)通过实验研究,专家们发现:初中学生听课的注意力指标数是随着老师讲课时间的变化而变化的,讲课开始时,学生的兴趣激增,中间有一段时间的兴趣保持平稳状态,随后开始分散.学生注意力指标数y随时间x(分钟)变化的函数图象如图所示(y越大表示注意力越集中).当0≤x≤10时,图象是抛物线的一部分,当10≤x≤20和20≤x≤40时,图象是线段.⑴当0≤x≤10时,求注意力指标数y与时间x的函数关系式;⑵一道数学综合题,需要讲解24分钟.问老师能否经过适当安排,使学生听这道题时,注意力的指标数都不低于36.
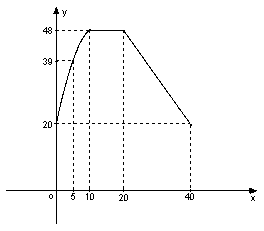 解(1)设0≤x≤10时的抛物线为y=ax2+bx+c,由图象知抛物线过(0,20),(5,39),(10,48)三点,∴
解(1)设0≤x≤10时的抛物线为y=ax2+bx+c,由图象知抛物线过(0,20),(5,39),(10,48)三点,∴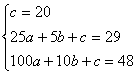 解得
解得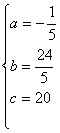 ∴
∴![]() ,(0≤x≤10)
,(0≤x≤10)
(2)由图象知,当20≤x≤40时,![]() ,当0≤x≤10时,令y=36,得
,当0≤x≤10时,令y=36,得![]() 解得x1=4,x2=20(舍去),当20≤x≤40时,另y=36,得
解得x1=4,x2=20(舍去),当20≤x≤40时,另y=36,得![]() ,解得
,解得![]() ∵
∵![]() -4=
-4=![]() >24 ∴老师可以通过适当的安排,在学生的注意力指标数不低于36时,讲授完这道数学综合题.
>24 ∴老师可以通过适当的安排,在学生的注意力指标数不低于36时,讲授完这道数学综合题.
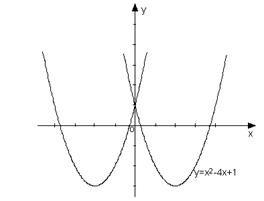 25.(2006年旅顺口区)已知抛物线y=x²—4x+1.将此抛物线沿x轴方向向左平移4个单位长度,得到一条新的抛物线.⑴求平移后的抛物线解析式;⑵若直线y=m与这两条抛物线有且只有四个交点,求实数m的取值范围;⑶若将已知的抛物线解析式改为y=ax²+bx+c(a>0,b<0),并将此抛物线沿x轴方向向左平移 -
25.(2006年旅顺口区)已知抛物线y=x²—4x+1.将此抛物线沿x轴方向向左平移4个单位长度,得到一条新的抛物线.⑴求平移后的抛物线解析式;⑵若直线y=m与这两条抛物线有且只有四个交点,求实数m的取值范围;⑶若将已知的抛物线解析式改为y=ax²+bx+c(a>0,b<0),并将此抛物线沿x轴方向向左平移 -![]() 个单位长度,试探索问题⑵.
个单位长度,试探索问题⑵.
解:(1) ![]() ,配方,得
,配方,得![]() ,向左平移4个单位,得
,向左平移4个单位,得![]() ∴平移后得抛物线的解析式为
∴平移后得抛物线的解析式为![]() ;(2)由(1)知,两抛物线的顶点坐标为(2,3),(-2,-3),解
;(2)由(1)知,两抛物线的顶点坐标为(2,3),(-2,-3),解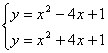 ,得
,得![]() ∴两抛物线的交点为(0,1) 由图象知,若直线y=m与两条抛物线有且只有四个交点时, m>-3且m≠1;(3)由
∴两抛物线的交点为(0,1) 由图象知,若直线y=m与两条抛物线有且只有四个交点时, m>-3且m≠1;(3)由![]() 配方得,
配方得,![]() 向左平移
向左平移![]() 个单位长度得到抛物线的解析式为:
个单位长度得到抛物线的解析式为:![]() ∴两抛物线的顶点坐标分别为
∴两抛物线的顶点坐标分别为![]() ,
,![]() , 解
, 解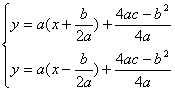 得,
得,![]() ,∴两抛物线的交点为(0,c) ,由图象知满足(2)中条件的m的取值范围是:m>
,∴两抛物线的交点为(0,c) ,由图象知满足(2)中条件的m的取值范围是:m>![]() 且m≠c 。
且m≠c 。
26.(2006年旅顺口区)直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于B、A两点.⑴求B、A两点的坐标;⑵把△AOB以直线AB为轴翻折,点O落在平面上的点C处,以BC为一边作等边△BCD求D点的坐标.
轴交于B、A两点.⑴求B、A两点的坐标;⑵把△AOB以直线AB为轴翻折,点O落在平面上的点C处,以BC为一边作等边△BCD求D点的坐标.
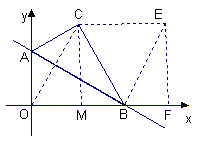 解:如图(1)令x=0,由
解:如图(1)令x=0,由![]() 得 y=1令y=0,由
得 y=1令y=0,由![]() 得
得![]() ∴B点的坐标为(
∴B点的坐标为(![]() ,0),A点的坐标为(0,1)。
,0),A点的坐标为(0,1)。
(2)由(1)知OB=![]() ,OA=1,∴tan∠OBA=
,OA=1,∴tan∠OBA=![]() =
=![]() ∴∠OBA=30°∵△ABC和△ABO关于AB成轴对称∴BC=BO=
∴∠OBA=30°∵△ABC和△ABO关于AB成轴对称∴BC=BO=![]() ,∠CBA=∠OBA=30° ∴ ∠CBO=60°,过点C作CM⊥x轴于M,则在Rt△BCM中,CM=BC×sin∠CBO=
,∠CBA=∠OBA=30° ∴ ∠CBO=60°,过点C作CM⊥x轴于M,则在Rt△BCM中,CM=BC×sin∠CBO=![]() ×sin60°=
×sin60°=![]() ,BM=BC×cos∠CBO=
,BM=BC×cos∠CBO=![]() ×cos60°=
×cos60°=![]() ∴OM=OB-BM=
∴OM=OB-BM=![]() -
-![]() =
=![]() ,∴C点坐标为(
,∴C点坐标为(![]() ,
,![]() ),连结OC,∵OB=CB,∠CBO=60°∴△BOC为等边三角形 。过点C作CE∥x轴,并截取CE=BC则∠BCE=60°。连结BE则△BCE为等边三角形.作EF⊥x轴于F,则EF=
CM=
),连结OC,∵OB=CB,∠CBO=60°∴△BOC为等边三角形 。过点C作CE∥x轴,并截取CE=BC则∠BCE=60°。连结BE则△BCE为等边三角形.作EF⊥x轴于F,则EF=
CM=![]() ,BF=BM=
,BF=BM=![]() ,OF=OB+BF=
,OF=OB+BF=![]() +
+![]() =
=![]() ,∴点E坐标为(
,∴点E坐标为(![]() ,
,![]() ) ∴D点的坐标为(0,0)或(
) ∴D点的坐标为(0,0)或(![]() ,
,![]() )。
)。
27.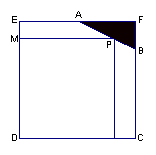 (2006年旅顺口区)已知边长为4的正方形截去一个角后成为五边形ABCDE(如图),其中AF=2,BF=1.试在AB上求一点P,使矩形PNDM有最大面积.
(2006年旅顺口区)已知边长为4的正方形截去一个角后成为五边形ABCDE(如图),其中AF=2,BF=1.试在AB上求一点P,使矩形PNDM有最大面积.
解:设矩形PNDM的边DN=x,NP=y
,则矩形PNDM的面积S= x y (2≤x≤4),易知CN=4-x ,EM=4-y,且有![]() ,即
,即![]() ,∴
,∴![]() , S= x y=
, S= x y=![]() ( 2≤x≤4)。此二次函数的图象开口向下,对称轴为x=5 ,∴当x≤5时,函数值是随x的增大而增大,对2≤x≤4来说,当x=4时,S有最大值, S最大=
( 2≤x≤4)。此二次函数的图象开口向下,对称轴为x=5 ,∴当x≤5时,函数值是随x的增大而增大,对2≤x≤4来说,当x=4时,S有最大值, S最大=![]() 。
。
28.(2006年旅顺口区)如图,我们给中国象棋棋盘建立一个平面直角坐标系(每个小正方形的边长均为1),根据象棋中“马”走“日”的规定,若“马”的位置在图中的点P.
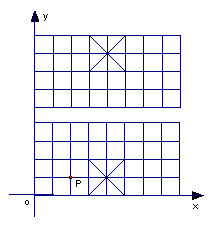 ⑴写出下一步“马”可能到达的点的坐标
⑴写出下一步“马”可能到达的点的坐标
;
⑵顺次连接⑴中的所有点,得到的图形是
图形(填“中心对称”、“旋转对称”、“轴对称”);
⑶指出⑴中关于点P成中心对称的点 .
(1)(0,0),(0,2),(1,3),(3,3),(4,2),(4,0);(2)轴对称 ;(3)(0,0)点和(4,2)点;(0,2)点和(4,0)点 。
29.(2006年贵阳市)已知点A(![]() ,2)在双曲线
,2)在双曲线![]() 上,则
上,则![]() ;
;![]()
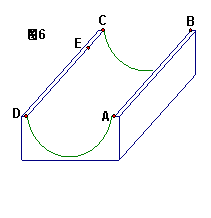 30.(2006年贵阳市)函数
30.(2006年贵阳市)函数![]() 与
与![]() 的图象如图5所示,这两个函数的交点在
的图象如图5所示,这两个函数的交点在![]() 轴上,那么
轴上,那么![]() 、
、![]() 的值都大于零的
的值都大于零的![]() 的取值范围是
;
的取值范围是
;![]()
31.(2006年贵阳市)某商场购进一种单价为40元的篮球,如果以单价50元出售,那么每月可售出500个,根据销售经验,售价每提高1元,销售量相应减少10个;
(1)假设销售单价提高![]() 元,那么销售每个篮球所获得的利润是
元;这种篮球每月的销售量是
个;(用含
元,那么销售每个篮球所获得的利润是
元;这种篮球每月的销售量是
个;(用含![]() 的代数式表示)(4分)
的代数式表示)(4分)
(2)8000元是否为每月销售这种篮球的最大利润?如果是,请说明理由;如果不是,请求出最大利润,此时篮球的售价应定为多少元?(8分)
 (1)
(1)![]() ,
,![]() ;
;
(2)设月销售利润为![]() 元,由题意得:
元,由题意得:![]() ,整理得:
,整理得:![]() ,当
,当![]() 时,
时,![]() 有最大值9000,
有最大值9000,![]() 。答:8000元不是最大利润,最大利润是9000元,此时篮球售价为70元。
。答:8000元不是最大利润,最大利润是9000元,此时篮球售价为70元。
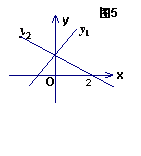
32.(2006年贵阳市)如图6,这是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是半径为![]() 的半圆,其边缘AB = CD =
的半圆,其边缘AB = CD =![]() ,点E在CD上,CE =
,点E在CD上,CE =![]() ,一滑板爱好者从A点滑到E点,则他滑行的最短距离约为
,一滑板爱好者从A点滑到E点,则他滑行的最短距离约为
![]() ;(边缘部分的厚度忽略不极,结果保留整数)22
;(边缘部分的厚度忽略不极,结果保留整数)22
33.(2006年贵阳市)小明根据邻居家的故事写了一首小诗:“儿子学成今日返,老父早早到车站,儿子到后细端详,父子高兴把家还。”如果用纵轴![]() 表示父亲与儿子行进中离家的距离,用横轴
表示父亲与儿子行进中离家的距离,用横轴![]() 表示父亲离家的时间,那么下面的图象与上述诗的含义大致吻合的是( )C
表示父亲离家的时间,那么下面的图象与上述诗的含义大致吻合的是( )C
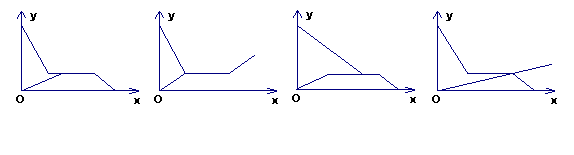
(A) (B) (C) (D)
34.(2006年江西省南昌市)近视眼镜的度数y(度)与镜片焦距x(m)成反比例,已知400度近视眼镜镜片的焦距为0. 25m,则y与x的函数是关系式为
![]() ;
;
(2006年江西省南昌市)若点A(2、n)在x轴上则 点B(n-2 ,n+1)在 【 】B
A第一象限 B第二象限 C第三象限 D第四象限
35.(2006年江西省南昌市)已知抛物线![]() ,经过点A(0,5)和点B(3 ,2)
,经过点A(0,5)和点B(3 ,2)
(1)求抛物线的解析式:
(2)现有一半径为l,圆心P在抛物线上运动的动圆,问⊙P在运动过程中,是否存在⊙P
与坐标轴相切的情况?若存在,请求出圆心P的坐标:若不存在,请说明理由;
(3)若⊙ Q的半径为r,点Q 在抛物线上、⊙Q与两坐轴都相切时求半径r的值
解:(1)由题意,得;![]() ,抛物线的解析式为
,抛物线的解析式为![]()
(2)当⊙P在运动过程中,存在⊙P与坐标轴相切的情况.设点P坐标为(![]() ),则
),则
则当⊙P与y轴相切时,有![]() =1,
=1,![]() =±1,由
=±1,由![]() = -1,得
= -1,得![]() ,由
,由![]() = 1,得
= 1,得![]()
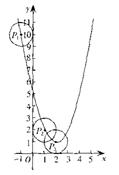 。
。
当⊙P与x轴相切时,有![]()
∵ 抛物线开口向上,且顶点在x轴的上方.∴![]() =1
=1
由![]() =1,得
=1,得![]() ,解得
,解得![]() =2,B(2,1)
=2,B(2,1)
综上所述,符合要求的圆心P有三个,其坐标分别为:
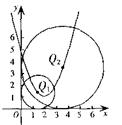
![]()
(3)设点Q坐标为(x,y),则当⊙Q与两条坐标轴都相切时,有y=![]() x
x
由y=x得![]() ,即
,即![]() ,解得
,解得![]()
由y=-x,得![]() .即
.即![]() ,此方程无解 。
,此方程无解 。
 ∴⊙O的半径为
∴⊙O的半径为 ![]()
36.(2006年江西省南昌市)如图,在平面直角坐标系中,点A在第一象限,点B的坐标为(3,0),OA=2,∠AOB=60°
(I) 求点A的坐标:
(2)若直线AB交x轴于点C,求△AOC的面积.
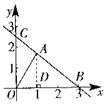 19.解:(1)过点A作AD⊥x轴,垂足为D,则OD=OA cos60°=2×
19.解:(1)过点A作AD⊥x轴,垂足为D,则OD=OA cos60°=2×![]() =1, AD=OA
sin60°=2×
=1, AD=OA
sin60°=2×![]() =
=![]() ,∴点A的坐标为(1,
,∴点A的坐标为(1,![]() )
)
(2)设直线AB的解析式为y=kx+b,则有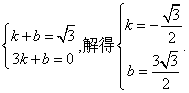
∴直线AB的解析式为![]() y。
y。
令x=0,得![]() ,∴
,∴![]() ,
, ![]()
37.(2006年南安市)近两年某地外向型经济发展迅速,一些著名跨国公司纷纷落户该地新区,对各类人才需求不断增加,现一公司面向社会招聘人员,其信息如下:
[信息一]招聘对象:机械制造类和规划设计类人员共150名.
[信息二]工资待遇:机械类人员工资为600元/月,规划设计类人员为1000元/月.
设该公司招聘机械制造类和规划设计类人员分别为x人、y人.
(1)用含x的代数式表示y;
(2)若公司每月付给所招聘人员的工资为p元,要使本次招聘规划设计人员不少于机械制造人员的2倍,求p的取值范围.
解:⑴y=150-x.⑵
根据题意,得:y≥2x,∴150-x≥2x, 解得:x≤50,又∵x≥0, 150-x≥0,∴0≤x≤50,∴p=600x+1000(150-x) =-400x+150000,(法一)∴x=![]() ,∴0≤
,∴0≤![]() ≤50, 解得:130000≤p≤150000;(法二)又∵p随x的增大而减小,并且0≤x≤50,∴-400×50+150000≤p≤-400×0+150000,即130000≤p≤150000 。
≤50, 解得:130000≤p≤150000;(法二)又∵p随x的增大而减小,并且0≤x≤50,∴-400×50+150000≤p≤-400×0+150000,即130000≤p≤150000 。
(2006年南安市)某商场将每件进价为80元的某种商品原来按每件100元出售,一天可售出100件.后来经过市场调查,发现这种商品单价每降低1元,其销量可增加10件.
(1)求商场经营该商品原来一天可获利润多少元?
(2)设后来该商品每件降价x元,,商场一天可获利润y元.
①若商场经营该商品一天要获利润2160元,则每件商品应降价多少元?
②求出y与x之间的函数关系式,并通过画该函数图像的草图,观察其图像的变化趋势,结合题
意写出当x取何值时,商场获利润不少于2160元?
解:⑴若商店经营该商品不降价,则一天可获利润100×(100-80)=2000(元);⑵ ①依题意得:(100-80-x)(100+10x)=2160,即:x![]() -10x+16=0 ,解得:x
-10x+16=0 ,解得:x![]() =2,x
=2,x![]() =8;经检验:x
=8;经检验:x![]() =2,x
=2,x![]() =8都是方程的解,且符合题意.答:商店经营该商品一天要获利润2160元,则每件商品应降价2元或8元.②依题意得:y=(100-80-x)(100+10x),∴y= -10x
=8都是方程的解,且符合题意.答:商店经营该商品一天要获利润2160元,则每件商品应降价2元或8元.②依题意得:y=(100-80-x)(100+10x),∴y= -10x![]() +100x+2000=-10(x-5)
+100x+2000=-10(x-5)![]() +2250,画草图(略),观察图像可得:当2≤x≤8时,y≥2160,∴当2≤x≤8时,商店所获利润不少于2160元.
+2250,画草图(略),观察图像可得:当2≤x≤8时,y≥2160,∴当2≤x≤8时,商店所获利润不少于2160元.
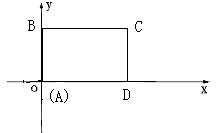 (2006年南安市)如图所示,在直角坐标系中,矩形ABCD的边AD在x轴上,点A在原点,AB=3,AD=5.若矩形以每秒2个单位长度沿x轴正方向作匀速运动.同时点P从A点出发以每秒1个单位长度沿A-B-C-D的路线作匀速运动.当P点运动到D点时停止运动,矩形ABCD也随之停止运动.
(2006年南安市)如图所示,在直角坐标系中,矩形ABCD的边AD在x轴上,点A在原点,AB=3,AD=5.若矩形以每秒2个单位长度沿x轴正方向作匀速运动.同时点P从A点出发以每秒1个单位长度沿A-B-C-D的路线作匀速运动.当P点运动到D点时停止运动,矩形ABCD也随之停止运动.
(1)求P点从A点运动到D点所需的时间;
(2)设P点运动时间为t(秒)。
①当t=5时,求出点P的坐标;
②若⊿OAP的面积为s,试求出s与t之间的函数关系式(并写出相应的自变量t的取值范围).
解:(1)P点从A点运动到D点所需的时间=(3+5+3)÷1=11(秒)
(2)①当t=5时,P点从A点运动到BC上,此时OA=10,AB+BP=5,∴BP=2。过点P作PE⊥AD于点E,则PE=AB=3,AE=BP=2,∴OD=OA+AE=10+2=12,∴点P的坐标为(12,3).
②分三种情况:i.当0<t≤3时,点P在AB上运动,此时OA=2t,AP=t,∴s=![]() ×2t×t= t
×2t×t= t![]() ;ii.当3<t≤8时,点P在AB上运动,此时OA=2t,∴s=
;ii.当3<t≤8时,点P在AB上运动,此时OA=2t,∴s=![]() ×2t×3=3t;iii.当8<t<11时,点P在CD上运动,此时OA=2t,AB+BC+CP=t,∴DP=(AB+BC+CD)-( AB+BC+CP)=11- t,∴s=
×2t×3=3t;iii.当8<t<11时,点P在CD上运动,此时OA=2t,AB+BC+CP=t,∴DP=(AB+BC+CD)-( AB+BC+CP)=11- t,∴s=![]() ×2t×(11-
t)=- t
×2t×(11-
t)=- t![]() +11t。综上所述,s与t之间的函数关系式是:当0<t≤3时,s=t
+11t。综上所述,s与t之间的函数关系式是:当0<t≤3时,s=t![]() ;当3<t≤8时,s=3 t;当8<t<11时,s=-t
;当3<t≤8时,s=3 t;当8<t<11时,s=-t![]() +11t。
+11t。
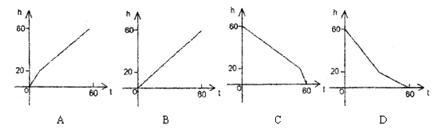
38.(2006年南安市)如图,一个蓄水桶,60分钟可将一满桶水放干.其中,水位h(cm)随着放水时间t(分)的变化而变化.h与t的函数的大致图像为( )C.
39.(2006年泰州市)反比例函数![]() 的图象在每个象限内,
的图象在每个象限内,![]() 随
随![]() 的增大而减小,则
的增大而减小,则![]() 的值可为D
的值可为D
A.![]() B.0
C.1
D.2
B.0
C.1
D.2
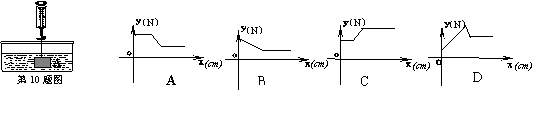
40.(2006年泰州市)在物理实验课上,小明用弹簧称将铁块A悬于盛有水的水槽中,然后匀速向上提起,直至铁块完全露出水面一定高度,则下图能反映弹簧称的读数y(单位N)与铁块被提起的高度x(单位cm)之间的函数关系的大致图象是C
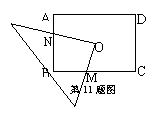
(2006年泰州市)如图,O为矩形ABCD的中心,将直角三角板的直角顶点与O点重合,转动三角板使两直角边始终与BC、AB相交,交点分别为M、N.如果AB=4,AD=6,O M=![]() ,ON=
,ON=![]() 则
则
![]() 与
与![]() 的关系是D
的关系是D
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
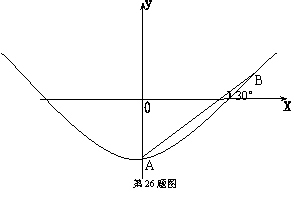 41.(2006年泰州市)如图,现有一横截面是一抛物线的水渠.一次,水渠管理员将一根长1.5
41.(2006年泰州市)如图,现有一横截面是一抛物线的水渠.一次,水渠管理员将一根长1.5![]() 的标杆一端放在水渠底部的A点,另一端露出水面并靠在水渠边缘的B点,发现标杆有1
的标杆一端放在水渠底部的A点,另一端露出水面并靠在水渠边缘的B点,发现标杆有1![]() 浸没在水中,露出水面部分的标杆与水面成30°的夹角(标杆与抛物线的横截面在同一平面内).
浸没在水中,露出水面部分的标杆与水面成30°的夹角(标杆与抛物线的横截面在同一平面内).
⑴以水面所在直线为![]() 轴,建立如图所示的直角坐标系,求该水渠横截面抛物线的解析式(结果保留根号);
轴,建立如图所示的直角坐标系,求该水渠横截面抛物线的解析式(结果保留根号);
⑵在⑴的条件下,求当水面再上升0.3![]() 时的水面宽约为多少?(
时的水面宽约为多少?(![]() 取2.2,结果精确到0.1
取2.2,结果精确到0.1![]() ).
).
42.(2006年泰州市)某市政府2007年准备投入一定资金加大对主城区的改造力度,但又不影响对教育及其他方面的投入.下面是市规划局等部门提供的信息:
①2007年用于主城区改造的资金不超过2007年教育投入的3.6倍.
②计划2007年比2006年的教育投入多0.5亿元,这样两年的教育投入之比为5:4.
③用于主城区改造的资金一部分由政府划拨,其余来源于招商引资.据分析发现,招商所引资金与政府划拨的资金始终满足某种函数关系.(如下表所示)
政府划拨资金与招商引进资金对照表(单位:亿元)
| 2002年 | 2003年 | 2004年 | 2005年 | |
| 政府划拨资金 | 1.2 | 1.4 | 1.5 | 1.6 |
| 招商引进资金 | 5.8 | 6.1 | 6.25 | 6.4 |
④2007年招商引资的投资者从2008年起每年共可获得0.67亿元的回报,估计2007年招商引进的资金至少10年方可收回.
⑴该市政府2006年对教育的投入为多少亿元?
⑵求招商引进资金y(单位:亿元)与财政划拨部分x(单位:亿元)之间的函数关系式.
 ⑶求2007年该市在主城区改造中财政划拨的资金的范围.
⑶求2007年该市在主城区改造中财政划拨的资金的范围.
29.
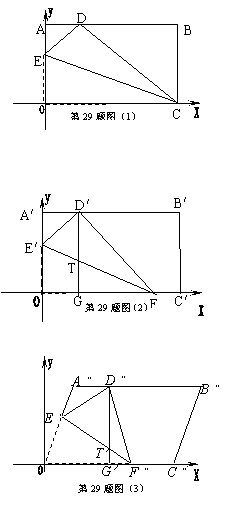
(2006年泰州市)将一矩形纸片OABC放在直角坐标系中,O为原点,C在![]() 轴上,OA=6,OC=10.
轴上,OA=6,OC=10.
⑴如图⑴,在OA上取一点E,将△EOC沿EC折叠,使O点落在AB边上的D点,求E点的坐标;
⑵如图⑵,在OA、OC边上选取适当的点E′、F,将△E′OF沿E′F折叠,使O点落在AB边上的D′点,过D′作D′G∥A′O交E′F于T点,交OC′于G点,求证:TG=A′E′
⑶在⑵的条件下,设T(![]() ,
,![]() )①探求:
)①探求:![]() 与
与![]() 之间的函数关系式.②指出变量
之间的函数关系式.②指出变量![]() 的取值范围.
的取值范围.
⑷如图⑶,如果将矩形OABC变为平行四边形OA"B"C",使O C"=10,O C"边上的高等于6,其它条件均不变,探求:这时T(![]() ,
,![]() )的坐标
)的坐标![]() 与
与![]() 之间是否仍然满足⑶中所得的函数关系,若满足,请说明理由;若不满足,写出你认为正确的函数关系式.
之间是否仍然满足⑶中所得的函数关系,若满足,请说明理由;若不满足,写出你认为正确的函数关系式.
(2006年苏州市)下列函数中,自变量x的取值范围是x>2的函数是 ( )C
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 43.(2006年苏州市)抛物线y=2x2+4x+5的对称轴是x=____ .一1;
43.(2006年苏州市)抛物线y=2x2+4x+5的对称轴是x=____ .一1;
(2006年苏州市)如图.围棋盘的左下角呈现的是一局围棋比赛中的几手棋.
为记录棋谱方便,横线用数字表示.纵线用英文字母表示,
这样,黑棋①的位置可记为(C,4),白棋②的位置可记为(E,3),
则白棋⑨的位置应记为 ______(D,6);
44.(2006年苏州市)已知函数y=![]() 和y=kx+l(k≠O).
和y=kx+l(k≠O).
(1)若这两个函数的图象都经过点(1,a),求a和k的值;
(2)当k取何值时,这两个函数的图象总有公共点?
(1) ∵两函数的图象都经过点(1,a),∴ ∴
∴![]()
(2)将y=![]()
![]() 代人y=kx+l,消去y.得kx2+x一2=0。∵k≠O,∴要使得两函数的图象总有公共点,只要△≥0即可。∵△=1+8k,∴1+8k≥0,解得k≥一
代人y=kx+l,消去y.得kx2+x一2=0。∵k≠O,∴要使得两函数的图象总有公共点,只要△≥0即可。∵△=1+8k,∴1+8k≥0,解得k≥一![]() 。∴k≥一
。∴k≥一![]() 且k≠0.
且k≠0.
45.(2006年苏州市)如图,直角坐标系中,已知点A(2,4),B(5,0),动点P从B点出发沿BO向终点O运动,动点O从A点出发沿AB向终点B运动.两点同时出发,速度均为每秒1个单位,设从出发起运动了![]() s.
s.
(1)Q点的坐标为(___,___)(用含x的代数式表示)
(2)当x为何值时,△APQ是一个以AP为腰的等腰三角形?
(3)记PQ的中点为G.请你探求点G随点P,Q运动所形成的图形,并说明理由.
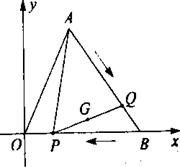
解:(1)(2+![]() ,4-
,4-![]() )。 (2)由题意,得P(5-x,0),0≤x≤5.由勾股定理,求得PQ2=(
)。 (2)由题意,得P(5-x,0),0≤x≤5.由勾股定理,求得PQ2=(![]() 一3)2+(4-
一3)2+(4-![]() )2,AP2=(3 -x)2+42,若AQ=AP,则x2=(3-x)2+42,解得x=
)2,AP2=(3 -x)2+42,若AQ=AP,则x2=(3-x)2+42,解得x=![]() ,若PQ=AP,则(
,若PQ=AP,则(![]() -3)2+(4-
-3)2+(4-![]() )2=(3-x)2+42,即
)2=(3-x)2+42,即![]() x2-10x=0,解得x1=0(舍去),x2=
x2-10x=0,解得x1=0(舍去),x2=![]() 。经检验,当x=
。经检验,当x=![]() 或x=
或x=![]() 时,△APQ是一个以AP为腰的等腰三角形.(3)解:设AB,BO的中点分别为点M,N,则点G随点P,Q运动所形成的图形是线段MN.证法一:由M(
时,△APQ是一个以AP为腰的等腰三角形.(3)解:设AB,BO的中点分别为点M,N,则点G随点P,Q运动所形成的图形是线段MN.证法一:由M(![]() ,2),N(
,2),N(![]() ,0),可求得线段MN的函数关系式为y=2x-5,(
,0),可求得线段MN的函数关系式为y=2x-5,(![]() ≤x≤
≤x≤![]() ),由P(5-x,0),Q(2+
),由P(5-x,0),Q(2+![]() ,4-
,4-![]() ),则G(
),则G(![]() ,G(
,G(![]() 满足y=2x-5 ∴点G在线段MN上.
满足y=2x-5 ∴点G在线段MN上.
证法二:设MN,PQ相交于点G/,过点P作PK∥AO交AB于点K.
∴PK∥AO∥MN.∴△A0B∽△KPB∽△MNB.∵AB=OB,∴BK=BP=AQ,BM=BN
∴BK-BM=AQ-BM.即KM=QM.∴PG/、=QG/,∴G/是PQ的中点,即点G/与点G重合.
46.(06年连云港市)(本小题满分12分)如图,已知抛物线y=px2-1与两坐标轴分别交于点A、B、C,点D坐标为(0,-2),△ABD为直角三角形,l为过点D且平行于x轴的一条直线。
(1)求p的值;
(2)若Q为抛物线上一动点,试判断以Q为圆心,QO为半径的圆与直线l的位置关系,并说明理由;
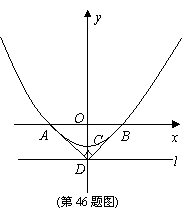 (3)是否存在过点D的直线,使该直线被抛物线所截得得线段是点D到直线与抛物线两交点间得两条线段的比例中项。如果存在,请求出直线解析式;如果不存在,请说明理由。
(3)是否存在过点D的直线,使该直线被抛物线所截得得线段是点D到直线与抛物线两交点间得两条线段的比例中项。如果存在,请求出直线解析式;如果不存在,请说明理由。
47.(06年连云港市)(本小题满分10分)如图,直线y=kx+2与x轴、y轴分别交于点A、B,点C(1,a)是直线与双曲线![]() 的一个交点,过点C作CD⊥y轴,垂足为D,且△BCD的面积为1。
的一个交点,过点C作CD⊥y轴,垂足为D,且△BCD的面积为1。
(1)求双曲线的解析式;
(2)若在y轴上有一点E,使得以E、A、B为顶点的三角形与△BCD相似,求点E的坐标。
48.(06年连云港市)函数![]() 中自变量x的取值范围是
中自变量x的取值范围是
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
49.(06年连云港市)用规格为50cm×50cm的地板砖密铺客厅恰好需要60块。如果改用规格为acm×acm的地板砖y块也恰好能密铺该客厅,那么y与a之间的关系为
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
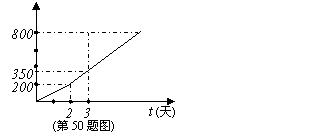
50.(06年连云港市)某农场租用收割机收割小麦,甲收割机单独收割2天后,又调来乙收割机参与收割,直至完成800亩的收割任务。收割亩数与天数之间的函数关系如图所示,那么乙参与收割的天数是
A、6天 B、5天 C、4天 D、3天