解直角三角形测试卷

　　　　　　　　 　　　　解直角三角形测试卷

班级　　　　  学号　　 姓名　　　　　  得分　　　

1、　填空：（16分）

（1）　  三角函数的定义：sinA＝　　　　　 　 cosA=　　　　　  

tanA=　　　　　　

（2）在△ABC中，∠C＝90°，，则cosB＝___________.

（3）Rt△ABC中，∠C＝90°，，则∠B＝_________度．

（4）△ABC中，∠C＝90°，，则AC＝_________.

（5）已知△ABC中，AB＝，∠B＝45⁰，∠C＝60⁰，AH⊥BC于H，则AH＝　　　；

CH＝　　　　　  ．

2、选择：（18分）

（1）在Rt△ABC中，如果一条直角边和斜边的长度都缩小至原来的，那么锐角A的各个三角函数值（　　）

　　A．都缩小　　　　B．都不变　　C．都扩大5倍　　 D．无法确定

（2）已知Rt△ABC中，∠C=90°，tanA=，BC=8，则AC等于（　）

　　A．6　　 B．　　  C．10　　　D．12

（3）已知∠A是锐角，且sinA=，那么∠A等于（　）

　　A．30°　　B．45°　　C．60°　　D．75°

（4）在Rt△ABC中，∠C=90°，已知α和A，则下列关系式中正确的是(　 )

（A）c=a·sinA（B）c=（C）c=a·cosA（D）c=

（5）某水库大坝的横断面是梯形，坝内斜坡的坡度，坝外斜坡的坡度，则两个坡角的和为　　　　　　　　　　　　　 　　　　　　　　　　（　　 ）

A、　　  B、　　　　C、　　　　D、

（6）在△ABC中，A，B为锐角，且有 ，则这个三角形是　　（　 　）

A、等腰三角形　B、直角三角形　C、钝角三角形　D、锐角三角形

3、（8分）计算：（1）sin45°+sin60°-2cos45°

（2）sin²30°+cos²45°+sin60°·tan45°；

4、（16分）根据下列条件解直角三角形.（Rt△ABC中，∠C=90⁰）

①　　　　 ②　=（边长保留3个有效数字，度数取整）

5、（10分） 已知：如图，在⊙O中，长为4cm,OA=3cm..求：

（1）∠AOB度数（精确到1度）

（2）AB的长度（精确到0.1）

（3）

6、　  （8分）如图：某同学用一个有60°角的直角三角板估测学校旗杆AB的高度，他将60°角的直角边水平放在1.5米高的支架CD上，三角板的斜边与旗杆的顶点在同一直线上，他又量得D、B的距离为5米，则旗杆AB的高度约为多少米。（精确到1米，取1.732）

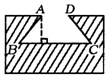
7、（8分）如图所示的燕尾槽一个等腰梯形，外口AD宽10cm，燕尾槽深10cm，AB的坡度i=1：1，求里口宽BC及燕尾槽的截面积．

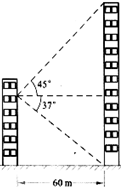
8、（8分）如图,物华大厦离小伟家60m,小伟从自家的窗中眺望大厦,并测得大厦顶部仰角是45^o ,而大厦底部的俯角是37^o ,求该大厦的的高度(结果精确到0.1m).

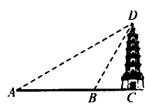9、（8分）如图，小明想测量塔CD的高度.他在A处仰望塔顶，测得仰角为30°，再往塔的方向前进50m至B处.测得仰角为60°.那么该塔有多高?(小明的身高忽略不计，结果精确到1 m)

10、附加题（20分）

（1）当锐角α>30°时，则cosα的值是（　）

　　A．大于　　 B．小于　　C．大于　　 D．小于

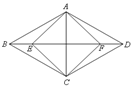
（2）如图，菱形ABCD中，点E、F在对角线BD上，BE=DF=BD，若四边形AECF为正方形，则tan∠ABE=_________．

（3）在Rt△ABC中，∠C＝90⁰，∠A、∠B的对边分别是、，且满足，则tanA等于（　　）

A、1　　　　  B、　　　　  C、　　　　　  D、

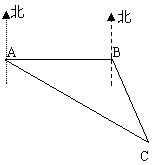
（4）台湾“华航”客机失事后，祖国大陆海上搜救中心立即通知位于A、B两处的上海救捞人局所属专业救助轮“华意”轮、“沪救12”轮前往出事地点协助搜索。接到通知后，“华意”轮测得出事地点C在A的南偏东60°、“沪救12”轮测得出事地点C在B的南偏东30°。已知B在A的正东方向，且相距100浬，分别求出两艘船到达出事地点C的距离。

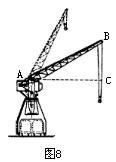
（5）如图8，一起重机的机身高21m，吊杆AB长36m，吊杆与水平线的夹角∠BAC可从30°升到80°．求起重机起吊的最大高度（吊钩本身的长度和所挂重物的高度忽略不计）和当起重机位置不变时使用的最大水平距离（精确到0.1米，sin80°=0.9848，cos80°=0.1736，