九年级第一学期数学期中学业评价试卷
学校_____________ 班级_____________ 姓名____________ 学号___________
一、精心选一选，你肯定很棒(40分)
1.有理式
，
（x+y）,
,
,
中，分式有（ ）个
A.1 B.2 C.3 D.4
2.下列运算中，计算结果正确的是（ ）
A、a2·a3= a6 B、（a-3）2= a6 C、a6÷a3=a2 D、
3.用科学记数法表示的数
(n为正整数)的整数位有( )
(A)n位 (B) n-1位 (C) n+1位 (D) n+2位
4．下列等式从左到右变形正确的是（ ）
A、
; B、
C、
;
D、
5..△ABC≌△DEF,且△ABC的周长为100 cm,A、B分别与D、E对应，且AB＝35 cm,DF=30 cm,则EF的长为 ( )
A.35 cm B.30 cm C.45 cm D.55 cm
6. 两圆的半径是方程x2-10x+9=0的两个根，若圆心距是8，则这两圆的位置关系是（ ）
A．相交 B．外切 C．内切 D．相离
7．用尺规作已知角平分线，其根据是构造两个三角形全等，它所用到的识别方法是（ ）
A．SAS B．ASA C．AAS D．SSS
8.已知方程x2-2
x+4cosa=0有两个相等的实数根，则锐角a=( )
A 30度 B 45度 C 60度 D无法确定．
9．如图所示，△ABC是不等边三角形，DE=BC，以D、E为两个顶点画位置不同的三角形，使所画的三角形与△ABC全等，这样的三角形最多可画出（ ）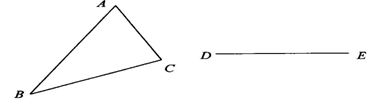
A．2个 B．4个 C．6个 D．8个
10．关于x的方程（m-1）x2-2mx+m=0有实数根，那么m的取值范围是（ ）
A．m>0 B．m≥0 C．m>0且m≠1 D．m≥0且m≠1
二、认真填一填，你一定能行（每小题5分，共30分）
11当x= 时，分式
的值为零
12把命题“平行四边形对边相等”改写成：如果……那么…
______________________________________________________
13.写出一个符合条件的一元二次方程：____________
使它的一个根X=1，且一次项系数为2.
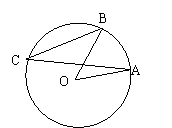
14、如图，在⊙O中，OA∥BC ，∠AOB=40O则∠A=________
15、半径为8的半圆围成一个圆锥，那么该圆锥的底面半径是________
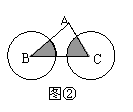
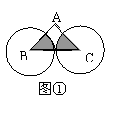
16如图①在△ABC中，∠A=90°，分别以B、C为圆心的等圆外切，
圆的半径为1，则图中阴影部分的面积为 ，图②若两圆外离，其他
条件不变，则阴影部分面积为
三、细心做一做，你一定很出色。
17.化简或计算（8分）
（1）
（2）
÷
18．（本题满分8分）
如图，点A、B、C表示三个村庄，现在建一座水泵站，
向三个村庄分别送水，为使三条输水管线长度相同，
水泵站应建在何处？请画出图形，并保留痕迹。
19.解方程.（8分）
(1)
=
2）用配方法解方程：-3x2-4x= -1
20(8分).已知如图：AB=AD，AC=AE，∠1=∠2，猜想∠1与∠3的大小关系，并证明你的猜
想。
21（10分）、已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.
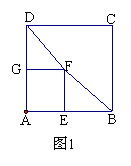
(1) 如图1, 连结DF、BF,判断命题:“线段DF与BF的长相等”是否正确,若正确请证明,若不正确请举反例说明;
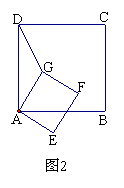
(2) 若将正方形AEFG绕点A按顺时针方向旋转, 连结DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等.并以图2为例说明理由.
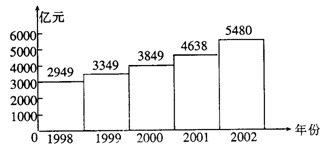
22．（12分）“国运兴衰，系于教育”图中给出了我国从1998─2002年每年教育经费投入的情况．
（1）由图可见，1998─2002年的五年内，我国教育经费投入呈现出_______趋势；
（2）根据图中所给数据，求我国从1998年到2002年教育经费的年平均数；
（3）如果我国的教育经费从2002年的5480亿元，增加到2004年7891亿元，那么这两年的教育经费平均年增长率为多少？（结果精确到0.01，
=1.200）
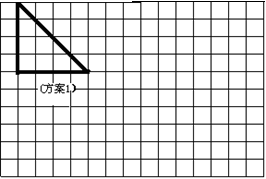
23（12分）．某车间利用直角边长为4的等腰直角三角形剩余材料进行产品加工。要在这个等腰直角三角形中剪出一个扇形，使扇形的半径都三角形的边上，且扇形的弧与三角形的其他边相切，
（1） 请在下列正方形网格中设计出尽可能多的形状不同、符合题意设计方案的示意图。
（2） 在你的设计方案中，你认为是方案几最能充分利用材料（扇形面积最大），并求出这个设计方案的扇形面积。
（3） 车间里还有其他边长为4的各种形状不同的等腰三角形，你还能从中找到符合设计要求，且面积不小于第（2）小题中最大面积的三角形吗？若存在，请求出这种三角形所设计的扇形的面积。若不存在，说明理由.
 |
24.（本题14分）如图1，已知
中，
，
．过点
作
，且
，连接
交
于点
．
（1）求
的长；
（2）以点为圆心，
为半径作⊙A，试判断与⊙A是否相切，并说明理由；
（3）如图2，过点
作
，垂足为
．以点为圆心，
为半径作⊙A；以点为圆心，
为半径作⊙C．若和的大小是可变化的，并且在变化过程中保持和⊙A和⊙C相切,且使D 点在⊙A的内部,点B在⊙A的外部,求r和R的变化范围.
 |
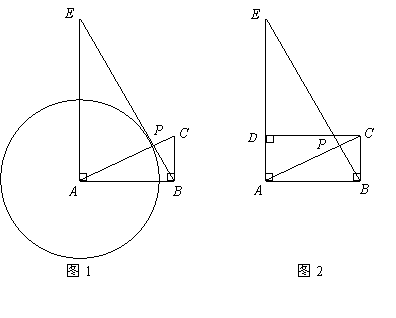参考答案
1选择题BDCAA CDCBB
2填空题 11。1/2 12。如果一个四边形是平行四边形那么它的对边相等。
13．略 14。20度 15。4 16。
,
3解答题
17．1/m-2 .x-3/x-2
18.略 19。（1） X=2是原方程的解 （2）
20．相等
证明：易证
得到∠B=∠D ∵∠BMA=∠DME ∴∠1=∠3
21. （1）正确。证明
得到DF=BF
（2）DG=BE 证明 
DAG≌BAE
22 （1）上升 （2）4053 （3）5480（1+X）2=7891 X≈20%
23．（1）
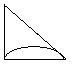
方案1 方案2 方案3 方案4
（2）方案1或方案2或方案3，最大扇形面积为
（平方单位）
（3）答：存在。
当三角形为等边三角形时，扇形面积=
（平方单位）
24.
在中，
，
．
，
．
．
，
．
（2）与
相切．
在
中，
，，
，
．
又
，
，
与相切．
（3）因为
，所以的变化范围为
．
当与
外切时，
，所以的变化范围为
；
当与内切时，
，所以的变化范围为
．