初三数学周周清（七）
命题人：杜福义
时间：90分 满分：100分 姓名
一、填空题（每小题3分，共30分）
1、
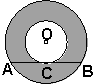如图，圆O的半径为R，则⊙O的外切正六边形的边长为
2、两个同心圆，大圆的弦AB切小圆于C，且AB＝12，则圆环的面积是
3、如图，点I是△ABC的内心，∠A＝80°，则∠BIC＝ °
4、如图，弓形半径为6，弓高为9，则弓形的面积是
5、小明向北走10米，左拐36°后继续走10米，再左拐36°
后继续走10米……，一直这样走下去，直到回到原地，他一共走了 米
6、正三角形的边心距、外接圆半径、高之比为___________
7、如图，△ABC中，AB＝AC，P是BC上任一点，画出△ACP绕点A顺时针
旋转∠BAC后的图形（用铅笔画，并保留作图痕迹）
8、圆锥的半径与母线长之比是1∶3，则展开图的圆心角是 。
9、在⊙O中，一条弦的长度等于半径，则这条弦所对的圆周角是 °
10、已知：如图，⊙O1与⊙O2外离，且O1A切⊙O2于A，O2B切⊙O1于点B，⊙O1与
⊙O2的半径分别为3cm与5cm。若O1A＝12cm，则O2B＝ cm
二、选择题（每小题3分，共30分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
1、 已知：某多边形的每个内角都是140°，则这个多边形是
A、正九边形 B、九边形 C、正十一边形 D、十一边形
2、
两圆内切，圆心距为3，一圆的半径为4，则另一圆的半径为
A、1 B、7 C、1或7 D、2
3、如图，正六边形两条平行边间的距离是1，则它的边长是
A、
B、
C、
D、
4、若两圆半径分别为R和r(R>r),圆心距为d,且R2+d2=r2+2Rd, 则两圆的位置关系为 A、内切 B、内切或外切
C、外切 D、相交
5、如图，一定滑轮的起重装置，滑轮半径为12cm，当重物上升4πcm时，滑轮的一条半径OA按逆时针方向旋转的度数为
A、12° B、30° C、60° D、90°
6、一个扇形半径30cm，圆心角120°，用它作一个圆锥的侧面，则圆锥底面半径为
A、5cm B、10cm C、20cm D、30cm
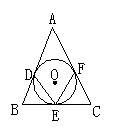
7、如图，△ABC的三边分别切⊙O于D，E，F，若∠A=50°，则∠DEF=
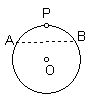A．65° B．50° C．130° D．80°
8、如图，⊙O为一张直径为6的圆形纸片，现将⊙O上的任意一点P与圆心O重合折叠后得折痕AB，则重叠部分图形的面积为
A、3π B、12π-
C、3π- D、
9、P为⊙O内一点，且OP=2
cm，过P的最长弦是6 cm，那么过P点的最短的弦等于
A、1 cm B、2 cm C、
cm D、2cm
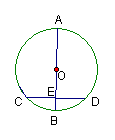
10、如图，在⊙O中，直径AB⊥弦CD于点E，若EB＝1
，CD＝4，则
弦心距OE的长为 A、 1.5 B、 2 C、3 D、 4
三、解答题
1、（8分）已知：AB是⊙O的直径，AC是弦，直线CE和⊙O切于点C，AD⊥CE于D，
求证：AC平分∠BAD
2、（8分）如图，BE是⊙O的直径，点A在EB的延长线上，弦PD⊥BE，垂足为C，连结OD，且∠AOD=∠APC. 求证：AP是⊙O的切线；
3、
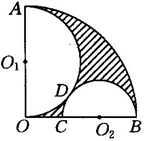（8分）如图，已知扇形AOB的半径为12，OA⊥OB，C为OB上一点，以OA为直线的半圆O与以BC为直径的半圆O相切于点D．求图中阴影部分面积．
4、如图，AB是半圆O的直径，点M是半径OA的中点，点P在线段AM上运动（不与点M重合）。点Q在半圆O上运动，且总保持PQ＝OP，过点Q作半圆O的切线交BA的延长线于点C。
⑴∠QPA＝60°时，请你对△QCP的形状做出猜想，并证明你的结论；
⑵当QP⊥AB时，△QCP是 三角形；
⑶由⑴、⑵得出结论，请进一步猜想当点P在线段AM上运动到任何位置时，△QCP一定是 三角形。
5、（8分）工厂有一批长为25㎝，宽为18㎝的矩形铝片，现要在一块铝片上截下一块最大的圆形铝片⊙O1，再在剩余的铝片上截下一个充分大的圆形铝片⊙O2，
你能求出⊙O1 ⊙O2的半径R，r的长吗？试一试！