初三数学自测题3
一、 选择题（每小题3分）
1、小敏在今年的校运动会跳远比赛中跳出了满意一跳，函数
(t的单位：s，h的单位：m)可以描述他跳跃时重心高度的变化，则他起跳后到重心最高时所用的时间是( )
(A)0.71s (B) 0.70s (C)0.63s (D)0.36s
2、已知抛物线的解析式为y＝(x－2)2＋1，则抛物线的顶点坐标是( )
A、(－2，1) B、(2，1) C、(2，－1) D、(1，2)
3、给出下列四个结论：①边长相等的四边形内角相等；②等腰梯形既是轴对称图形又是中心对称图形；③三角形的内切圆和外接圆是同心圆；④圆心到直线上一点的距离恰好等于圆的半径，则该直线是圆的切线。其中正确结论的个数有( )
(A) 0 个 (B) 1个 (C) 2个 (D) 3个
4、一个扇形的圆心角是120°，它的面积为3πcm2，那么这个扇形的半径是( )
A、
cm Ｂ、3cm Ｃ、6cm Ｄ、9cm
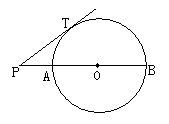
5、如图，PT切⊙O于点T，经过圆心O的PB交⊙O于点A、B，已知PT＝4，PA＝2，则⊙O的直径AB等于( )
A、3 B、4 C、6 D、8
6、直线l与半径为r的⊙O相交，且点O到直线l的距离为5，则r的取值范围是（ ）
A、r>5 B、r=5 C、r<5 D、r≤5
7、下列事件是随机事件的是（ ）
（A）两个奇数之和为偶数， （B）某学生的体重超过200千克，
（C）宁波市在六月份下了雪， （D）三条线段围成一个三角形。
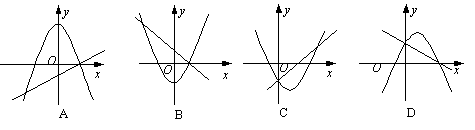
8、下面所示各图是在同一直角坐标系内，二次函数
与一次函数
的大致图象，有且只有一个是正确的，正确的是（ ）
二、填空题（每小题3分）
9、袋中装有3个白球，2个红球，1个黑球，从中任取1个，那么取到的不是红球的概率是 ；
10、某射手在同一条件下进行射击，结果如下表所示：
| 射击次数（n） | 10 | 20 | 50 | 100 | 200 | 500 | … |
| 击中靶心次数(m) | 8 | 19 | 44 | 92 | 178 | 455 | … |
| 击中靶心频率（） |
|
|
|
|
|
| … |
请填好最后一行的各个频率，由此表推断这个射手射击1次，击中靶心的概率的是
11、已知⊙O1和⊙O2相外切，且圆心距为10cm，若⊙O1半径为3cm，则⊙O2的半径为__________cm.
12、二次函数
y=x2 的图像向下平移2个单位，再向右平移3个单位后图像的函数表达式为
13、半径为2的圆内接正六边形的边心距等于 。
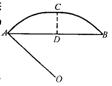
14、如图，有一圆弧形桥拱，拱形的半径OA=10m，桥拱的
跨度AB=16m，则拱高CD=_____________m。
15、请写出一个开口向上，对称轴为直线x=2，且与y轴的交点坐标
为(0，3)的抛物线的解析式 y=(x－2)2＋3等 。
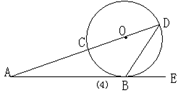16、如图(4)，CD是⊙O的直径，AE切⊙O于B，DC的延长线交AB于A，
∠A＝200，则∠DBE＝＿＿ ＿＿＿＿。
二、 简答题（每小题6分）
17、某养鱼户春季在鱼塘中放养鱼苗10万尾，9月份进行一次试捕320条，测得平均体重0.82kg，对每条鱼做好标记后，放回鱼塘，继续饲养；过了20天，进行第二次试捕，共捕鱼300条，其中仅一条有标记，这一次测得平均体重是1.02kg
（1） 根据以上数据，估计鱼苗的成活率
（2） 根据以上数据，估计鱼塘中每条鱼增重多少；
（3） 若再过30天，恰逢节日，鱼价将达到每kg5元，问该养鱼户将所有的鱼一次捕捞上市，可以收入多少元？
18、某电脑公司现有A，B，C三种型号的甲品牌电脑和D，E两种型号的乙品牌电脑．希望中学要从甲、乙两种品牌电脑中各选购一种型号的电脑．
(1) 写出所有选购方案(利用树状图或列表方法表示)；
(2) 如果(1)中各种选购方案被选中的可能性相同，那么A型号电脑被选中的概率是多少？
(3) 现知希望中学购买甲、乙两种品牌电脑共36台(价格如图所示)，恰好用了10万元人民币，其中甲品牌电脑为A型号电脑，求购买的A型号电脑有几台．
19、例3、圆心角都是90°的扇形OAB与扇形OCD如图所示那样叠放在一起，连结AC、BD．
(1) 求证：△AOC≌△BOD；
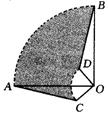(2) 若OA＝3cm，OC＝1cm，求阴影部分的面积．
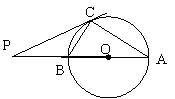20、如图，AB是⊙O的直径，P是AB的延长线上的一点，PC切⊙O于点C ，⊙O的半径为3，
．
⑴求
的度数；⑵求PA的长．
21、如图，A、B、C、三点表示平原上的三个村庄，要建一个电视转播站，使它到三个村庄的距离相等，求电视转播站的位置P。（尺规作图，只保留作图痕迹）
作图：
要将如图所示的破圆轮残片复制完成,怎样确定这个圆轮残片的圆心和半径?(写出找圆心和半径的步骤).
22、．如图，一位运动员在距篮下4米处跳起投篮，球运行的路线是抛物线，当球运行的水平距离为2.5米时，达到最大高度3.5米，然后准确落入篮圈，已知篮圈中心到地面的距离为3.05米。
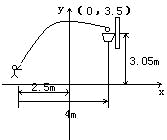建立如图所示的直角坐标系，求抛物线的解析式。
三、 解答题（每小题8分（）
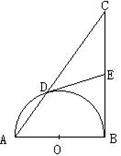
23、如图，以Rt△ABC的直角边AB为直径的半圆O，与斜边AC交于D，E是BC边上的中点，连结DE.
(1) DE与半圆O相切吗？若相切，请给出证明；若不相切，请说明理由；
(2) 若AD、AB的长是方程x2－10x+24=0的两个根，求直角边BC的长。
24、已知抛物线的顶点坐标是（－2，1），且过点（1，－2），求抛物线的解析式。
四、 综合题（每小题10分）
25、如图，已知直角梯形ABCD中，AD∥BC，∠A=90o，∠C=60o，AD=3cm，BC=9cm．⊙O1的圆心O1从点A开始沿A—D—C折线以1cm/s的速度向点C运动，⊙O2的圆心O2从点B开始沿BA边以
cm/s的速度向点A运动，如果⊙O1半径为2cm，⊙O2的半径为4cm，若O1、O2分别从点A、点B同时出发，运动的时间为ts
(1)请求出⊙O2与腰CD相切时t的值；
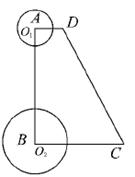(2)在0s<t≤3s范围内，当t为何值时，⊙O1与⊙O2外切？
26如图，在直角坐标系中，以x轴上一点P（1，0）为圆心的圆与x轴，
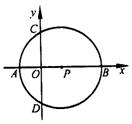y轴分别交于A、B、C、D四点，点C的坐标为（0，）．
（1）直接写出A、B、D三点坐标；
（2）若抛物线
过A、D两点，求这条抛物线的解析式，
判断点B是否在所求的抛物线上，说明理由。