九年级数学下学期期终考试试卷
时量：120分钟，满分：120分
| 题次 | 一 | 二 | 三 | 四 | 五 | 六 | 总分 | 合分人 |
| 得分 |
卷首寄语：人有信心虽然不一定能赢，但没有信心是一定会输的。
同学：希望你树立信心，迎难而上，胜利将一定会属于你的！
| 得分 | 评卷人 | 复评人 |
一、细心填一填（每小题3分，共30分）
1、a8÷a2＝
2、约分＝
3、一元二次方程(2x-1)2-7＝x化为一般形式
4、方程x2＝x的根是
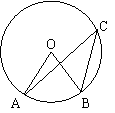
5、如图1，点A、B、C在⊙O上，∠ACB＝25°，
则∠AOB＝ 。
|
该圆锥的侧面积是
。
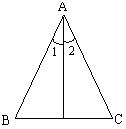
7、已知如图2，△ABC中，D在BC上，且∠1＝
∠2，请你在空白处填一个适当的条件：当 时，
则有△ABD≌△ACD。
8、将“等腰三角形两底角相等”改写成“如果……，那么……”的形式是
。
9、掷一枚普通的正方体骰子，出现点数为偶数的概率为 。
10、一段时间里，某学生记录了其中7天他每天完成家庭作业的时间，结果如下（单位：分钟）80、90、70、60、50、80、60，那么在这段时间内该生平均每天完成家庭作业所需时间约为 分钟。
| 得分 | 评卷人 | 复评人 |
二、认真选一选。（将每小题内唯一正确的答案代号填入下表中相应的答题栏内，每小题3分，共30分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
11、计算2006°＋()-1的结果是：
A、2006 B、2009 C、4 D、
12、分式，的最简公分母是：
A、(a-x)(ay-xy) B、a(a-x)
C、y(a-x) D、a-x
13、若x＝1是方程x2＋kx＋2＝0的一个根，则方程的另一个根与K的值是：
A、2，3 B、－2，3 C、－2，－3 D、2，－3
14、三角形的外心是指：
A、三角形三角平分线交点 B、三角形三条边的垂直平分线的交点
C、三角形三条高的交点 D、三角形三条中线的交点
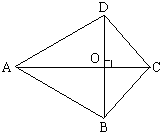15、已知如图3，AC是线段BD的垂直平分线，
则图中全等三角形的对数是：
A、1对 B、2对
C、3对 D、4对
16、能判定两个直角三角形全等的是：
A、有一锐角对应相等 B、有两锐角对应相等
C、两条边分别相等 D、斜边与一直角边对应相等
17、两圆半径分别是7和3，圆心距是4，则这两圆的位置关系是：
A、内含 B、内切 C、相交 D、外切
18、一扇形面积是3π，半径为3，则该扇形圆心角度数是
A、120° B、90° C、60° D、150°
19、从总体中抽取一部分数据作为样本去估计总体的某种属性，下面叙述正确的是
A、样本容量越大，样本平均数就越大
B、样本容量越大，样本的标准差就越大
C、样本容量越小，样本平均标准差就越大
D、样本容量越大，对总体的估计就越准确。
20、“闭上眼睛从一布袋中随机摸出1球是红球的概率是”，表示：
A、摸球6次就一定有一次摸中红球
B、摸球5次就一定有5次不能摸中红球
C、布袋中有一个红球与5个其它颜色的球
D、若摸球次数很多，那么平均每摸球6次就有1次摸中红球
| 得分 | 评卷人 | 复评人 |
三、好好画一画：（本题8分，要求利用尺规作图，不写画法，但需保留作图痕迹）
21、（1）画出∠AOB的角平分线； （2）作线段AB的垂直平分线。
| 得分 | 评卷人 | 复评人 |
四、精心解一解（友情提示：本题不难，但要细心，每小题6分，共24分）
22、计算：＋·
23、解方程：x2―3x―2＝0
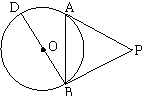
24、如图4，PA·PB分别切⊙O于A、B，∠APB＝50°，BD是⊙O的直径，
求∠ABD的大小。
 | |||
| |||
25、已知：如图5，OA＝OC，OB＝OD，试说明：△AOB≌△COD
 | |||
| |||
| 得分 | 评卷人 | 复评人 |
五、仔细想一想。（本题8分）
26、2005年长沙市春季马路赛跑中，共有2000名运动员为参赛选手，其中设一等奖50名，二等奖100名，三等奖150名，四等奖200名，纪念奖500名。
①小明参赛回来说他已获奖，且他获奖的那个等级的获奖概率是，请问他获得了几等奖？为什么？
②小刚参赛回来说他的成绩排在参赛选手的前，那么他有可能获得哪些等级的奖励呢？
| 得分 | 评卷人 | 复评人 |
六、迎难闯一闯。（本题共20分，其中27题8分，28题12分）
27、小李在家润多超市购买一种商品，与营业员有一段对话：
小李：上个月买还要90元一个，而这次便宜多3，一次降价幅度达到19%，营业员：不，这中间还降了一次价，两次降价幅度相同。
请你帮小李算一算，该商品平均每次降价的百分率是多少？
28、如图6，已知直线AB与x轴、y轴分别交于A和B，OA＝4，且OA、OB长是关于x的方程x2－mx＋12＝0的两实根，以OB为直径的⊙M与AB交于C，连结CM并延长交x轴于N。
（1）求⊙M的半径。
（2）求线段AC的长。
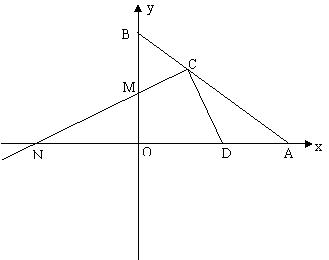（3）若D为OA的中点，求证：CD是⊙M的切线
九年级数学下学期期终考试试卷参考答案及评分标准
一、1、a6 2、 3、7 4、0，1 5、50°
6、12πcm2
7、可填：∠B＝∠C ∠ADB＝∠ADC AD⊥BC AB＝AC
8、略 9、 10、70
二、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | C | D | B | C | D | B | A | D | D |
三、21、每小题4分 略
四、22、原式= + · (1分)
= －· （2分）
= － （4分）
= 0 （6分）
23、
24、解：∵ PA·PB是切线
∴ PA＝PB
∴ ∠PBA＝（180°－50°）÷2 = 65° （3分）
∵ BD是直径
∴ BD⊥PB （4分）
∴∠ABD＋∠PBA = 90° （5分）
∴∠ABD = 25°
25、略
26、①四等奖（2分）
∵ = （4分）
② 获一、二、三、四等奖都有可能 （8分）
27、设每次降价百分率为x （1分）
∴ 90(1－x)2 = 90（1－19%） （4分）
∴ x1 = 1.9（舍去）
x2 = 0.1 = 10% （7分）
答：略 （8分）
28、（1）∵OA = 4 ∴A（4，0）
又OA·OB长是x2－mx＋12＝0的两根
∴ OA·OB＝12 ∴OB = 3 故B（0，3） （2分）
∵OB为直径
∴半径MB = （4分）
（2）连结OC
∵OB是⊙M直径
∴OC⊥BC （5分）
∴OC·AB = OA·OB
∵AB = = 5 （6分）
∴OC·5＝3·4
∴OC＝ （7分）
∴ AC＝＝ （8分）
（3）∵OM = OC ∴∠MOC＝∠MCO (9分)
又CD是Rt△OCA斜边上中线
∴ DC＝DO
∴∠DOC＝∠DCO （10分）
∵∠DOC＋∠MOC＝90°
∴∠MCO＋∠DCO＝90°
∴DC⊥MC （11分）
∴CD是⊙M的切线 （12分）
（注：由于解法不一，可以视方法的异同与合理性分步计分）