九年级数学学业检测试卷
一、选择题（各小题中只有一项是正确的，每小题4分，共40分）
1、一元二次方程
的两个根分别为( )．
A、Xl=1， x2=3 B、Xl=1， x2=-3 C、X1=-1，X2=3 D、XI=-1， X2=-3
2、下列图形中，既是中心对称图形，又是轴对称图形的是（ ）、
A、等腰三角形 B、等边三角形 C、平行四边形 D、菱形
3、某几何体的三种视图分别如下图所示，那么这个几何体可能是（ ）。
A、 空心长方体 B、圆柱
C、 圆锥 D、圆台
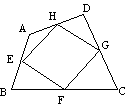
4、如图，E、F、G、H分别是四边形ABCD四条边的中点，要使四边形EFGH为矩形，四边形ABCD应具备的条件是（ ）
A、一组对边平行而另一组对边不平行 B、对角线相等
C、对角线互相垂直 D、对角线互相平分
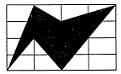
5、如图是某广告公司为某种商品设计的商标图案，若图中每个小长方形的面积都是1，则阴影部分的面积是（ ）
A、6 B、6.5 C、7 D、7.5
6、若甲杆高1米，它在地面上的影长为0.8米，但在同一时刻去测量乙杆的影长时，因乙杆靠近墙壁，故其影子没有全落在地面上，有一部分留在了墙壁上，测得留在墙壁上的影高1.2米，又测得它留在地面上的影长为2.4米，则乙杆的长是（ ）
A、3米 B、4.2米 C、4.5米 D、不能确定
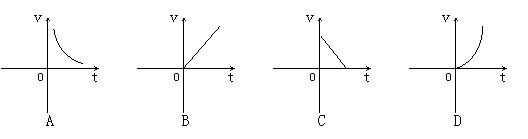7、在匀速运动中，路程s(千米)一定时，速度v(千米/时)关于时间t(小时)的函数关系的大致图象是（ ）
（第4题图） （第5题图） （第8题图）
8、某装饰公司要在如图所示的五角星型中，沿边每隔20厘米装一盏闪光灯。
若BC=（√5－1）米，则共需安装闪光灯（ ）
A、100盏 B、101盏 C、102盏 D、103盏
9、在平面直角坐标系中，已知A（2，－2），在y轴上确定点P，使△AOP为等腰三角形，（O为坐标原点）则符合条件的点P共有（ ）
A、2个 B、3个 C、4个 D、5个
 |
10、已知反比例函数 的图象上有两点A（x1，y1）和B（x2，y2），且x1＜x2，那么下列结论正确的是（ ）
A、y1＜y2 B、y1＞y2 C、y1 = y2 D、y1与y2之间的大小关系不能确定
二、填空题（每小题5分，共30分）
 |
11、已知反比例函数 的图象在第二、四象限内，则k的值可以为 (写出满
足条件的一个k的值即可)
12、已知：在等腰梯形ABCD中，AD∥BC，对角线AC⊥BD,AD=3cm,BC=7cm,则梯形的高是____ cm。
13、如图是利用四边形不稳定性制作的可活动菱形晾衣架，已知其中每个菱形的边长为15cm，∠1= 600，则在墙上悬挂晾衣架的两个铁钉A和B之间的距离为 cm。
14、在ΔABC中，AB= 4，AC= 2√2，∠B= 300，则∠BAC的度数是 。
15、利用旧墙(旧墙长为7m)为一边，再用13米长的篱笆围成一个面积为20m²的长方形场地，则长方形场地的长和宽分别是是 m。
16、用边长为1cm的小正方形搭如下的塔状图形，则第n次所搭图形的周长
是 _ cm（用含n的代数式表示）
 | |||
 | |||
···
第1次 第2次 第3次 第4次 ···
三、解答题（本部分共8大题，其中第17-20题每题8分，第21题10分，第22、23每题12分，第24题14分，共80分）
17、对于二次三项式x2－10x+36，小聪同学作出如下结论：无论x取什么实数，它的值都不可能等于11．你是否同意他的说法？说明你的理由．
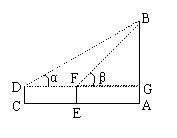
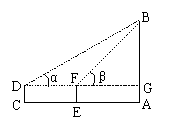
18、如图,在C处用测角仪测得塔AB顶端B的仰角α=30°，向塔的方向前进20米到E处，又测得塔顶端B的仰角β= 45°，已知测角仪高1.20米，求塔AB的高(精确到0.1米)。
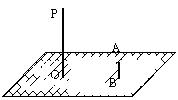19、如图，晚上小亮在广场上乘凉。图中线段AB表示站在广场上的小亮，线段PO表示直立在广场上的灯杆，点P表示照明灯。
⑴请你在图中画出小亮在照明灯P照射下的影子
⑵如果灯杆高PO=12m，小亮的身高AB=1.6m，小亮与灯杆
之间的距离BO=13m，请求出小亮影子的长度。
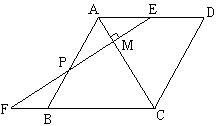20、如图，已知在菱形ABCD 中，E为边AD的中点，EF⊥AC交CB的延长线于点F，交AB于点P，交AC于点M，求FM／EF的值。
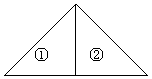
21、正方形通过剪切(虚线为剪切线) 可以拼成三角形,方法如下:
 | |||
 | |||
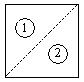剪切线为对角线
仿照上述图示方法,解答下列操作设计问题:
(1)如图(1),对直角三角形,设计一种方案,将它分成2块, 拼成一个与原三角形等面积的矩形。（剪切线用虚线表示）
(2)如图(2),对任意三角形,设计一种方案,将它分成若干块, 拼成一个与原三角形等面积的矩形。（剪切线用虚线表示）
图(1) 图(2)
22、已知一次函数y =
mx+n与反比例函数
的图象相交于点A（ ，，2）。
⑴求这两个函数的图象的另一个交点B的坐标。
⑵设O为坐标原点，求△AOB的面积。
⑶利用两个函数图象的草图回答：当x满足什么条件时，一次函数的函数值大于反比例函数的函数值？（本小题直接写出x的范围，不必写出解题过程）
23、如图，已知在□ABCD 中，E、F分别为边AB、CD的中点，BD是对角线，AG∥DB交CB的延长线于G。
（1）求证：△ADE≌△CBF
（2）若四边形 BEDF是菱形，则四边形AGBD是什么特殊四边形？并证明你的结论。
 |
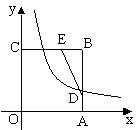
24、如图在直角坐标系xoy中,正方形OABC的边长为4cm,点A、C分别在x轴、y轴的
 |
正半轴上。双曲线 （x＞0）经过点（1，5）。
（1）求双曲线的解析式。
（2）点D、E分别是AB、BC上的动点，且点D从点A开始，以1cm／s的速度沿AB向点B移动，同时点E从点B开始，以1cm／s的速度沿BC向点C移动，运动t（≦4）秒后，回答下列问题：
①当∠EDB=300时，求点E的坐标。
②能否在双曲线上找到一点P，使得以B、E、D、P四点为顶点的四边形为平行四边形？如果能，请求出t的值和点P的坐标；如果不能，请说明理由。
 |
九年级数学学业检测答题卷
一、选择题（每小题4分，共40分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题（每小题5分，共30分）
11、 12、 13、
14、 15、 16、
三、解答题（共9小题，共80分）
17、
18、
19、
|
20、
21、
 |
图(1)
 | |||
| |||
图(2)
22、
|
23、
24、