九年级数学第24章整章水平测试
一、填空题(每小题3分,共30分)
1.如图1,已知![]() ,则
,则![]() 的理由是 .
的理由是 .
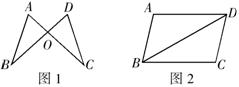 |
2.如图2,已知![]() ,则
,则![]() .
.
 3.如图3,已知
3.如图3,已知![]() ,根据
,根据![]() 全等识别法,要使
全等识别法,要使![]() ,只需增加的条件是 .
,只需增加的条件是 .
4.如图4,在![]() 中,
中,![]() ,且
,且![]() ,将
,将![]() 顺时针旋转 度后能与 重合,所以
顺时针旋转 度后能与 重合,所以![]() .
.
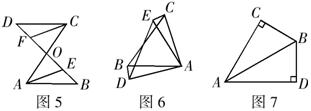 5.如图5,线段
5.如图5,线段![]() 和
和![]() 相交于点
相交于点![]() ,且
,且![]() ,则图中有 对全等三角形.
,则图中有 对全等三角形.
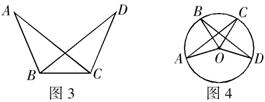
6.如图6,把等腰![]() 绕顶点
绕顶点![]() 逆时针旋转某个角度后得
逆时针旋转某个角度后得![]() ,连结
,连结![]() ,则根据全等三角形的识别方法 ,可得到
,则根据全等三角形的识别方法 ,可得到![]() ,从而
,从而![]() .
.
7.如图7,在![]() 和
和![]() 中,
中,![]() ,要使
,要使![]() ,还需增加一个条件 .(只填一个你认为正确的条件即可)
,还需增加一个条件 .(只填一个你认为正确的条件即可)
8.将命题“对顶角相等”写成“如果……,那么……”的形式是 .
9.命题“平行于同一直线的两条直线平行”的结论是 .
10.等腰直角三角形![]() 中,
中,![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,则
,则![]() 边上的高为 .
边上的高为 .
二、选择题(每小题2分,共20分)
1.下列命题中是真命题的是( )
A.相等的圆心角所对的弧相等 B.等弧所对的圆心角相等
C.相等的圆心角所对的弦相等 D.圆周角等于圆心角度数的一半
2.如图8所示,在![]() 中,
中,![]() ,
,![]() 为
为![]() 的中线,那么下列结论错误的是( )
的中线,那么下列结论错误的是( )
A.![]() B.
B.![]()
C.![]() 是
是![]() 的高 D.
的高 D.![]() 是等边三角形
是等边三角形
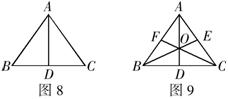
3.如图9所示,在![]() 中,
中,![]() ,
,![]() 交于点
交于点![]() ,且分别交
,且分别交![]() 于
于![]() 三点,已知
三点,已知![]() 为
为![]() 中点,则图中全等三角形的对数是( )
中点,则图中全等三角形的对数是( )
A.7 B.6 C.5 D.4
4.下列作图语中正确的是( )
A.过![]() 三点作直线 B.延长线段
三点作直线 B.延长线段![]()
C.以点![]() 为圆心作一弧 D.以线段
为圆心作一弧 D.以线段![]() 为直径作半圆
为直径作半圆
5.在![]() 和
和![]() 中,①
中,①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,⑤
,⑤![]() ,⑥
,⑥![]() ,下列条件中,不能保证
,下列条件中,不能保证![]() 的是( )
的是( )
A.①②③ B.①②⑤ C.②④⑤ D.①③⑤
6.如图10,点![]() 分别在
分别在![]() 上,且
上,且![]() ,那么补充下列一个条件后仍无法判断
,那么补充下列一个条件后仍无法判断![]() 的是( )
的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
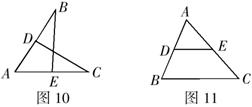 |
7.如图11,![]() 为
为![]() 的边
的边![]() 的中点,过点
的中点,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,要使
上,要使![]() 和
和![]() 全等,符合条件的点
全等,符合条件的点![]() 的个数为( )
的个数为( )
A.4个 B.3个 C.2个 D.1个
8.下列说法正确的是( )
A.假命题不是命题 B.真命题是定理
C.公理是真命题 D.以上说法都不正确
9.如图12,![]() 是不等边三角形,
是不等边三角形,![]() ,以
,以![]() 为两个顶点作位置不同的三角形,使所作的三角形与
为两个顶点作位置不同的三角形,使所作的三角形与![]() 全等,这样的三角形最多可以画出( )
全等,这样的三角形最多可以画出( )
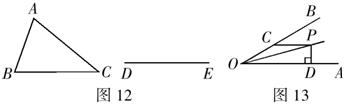 A.2个 B.4个 C.6个 D.8个
A.2个 B.4个 C.6个 D.8个
10.如图13,![]() ,若
,若![]() ,则
,则![]() 等于( )
等于( )
A.4 B.3 C.2 D.1
三、解答题(本大题共70分)
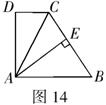
1.(本题10分)如图14,![]() ,垂足分别为点
,垂足分别为点![]() ,
,![]() ,又
,又![]() ,垂足为
,垂足为![]() .求证:
.求证:![]() .
.
 |
2.(本题10分)如图15,已知线段![]() ,求作:
,求作:![]() ,使
,使![]() (用尺规作图,保留作图痕迹).
(用尺规作图,保留作图痕迹).
 |
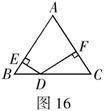
3.(本题10分)如图16,已知![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上的一点,
边上的一点,![]() ,垂足分别为点
,垂足分别为点![]() ,当点
,当点![]() 在什么位置时,
在什么位置时,![]() .并加以证明.
.并加以证明.
 |
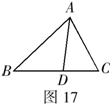
4.(本题12分)如图17,![]() 为
为![]() 的角平分线,
的角平分线,![]() .求证:
.求证:![]() .
.
 |
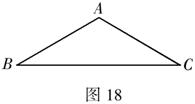
5.(本题14分)图18是一个三角形纸片,其中![]() ,请设计三种不同的剪法,将
,请设计三种不同的剪法,将![]() 剪成四个三角形,使得其中两个是全等三角形,而另外两个是相似但不全等的直角三角形,请画出分割线段,标出能够说明剪法的所得三角形的顶点和内角度数,并在各种剪法的空格线上填空(画图工具不限,不要求写画法,也不证明).
剪成四个三角形,使得其中两个是全等三角形,而另外两个是相似但不全等的直角三角形,请画出分割线段,标出能够说明剪法的所得三角形的顶点和内角度数,并在各种剪法的空格线上填空(画图工具不限,不要求写画法,也不证明).
(注:两种剪法只要有一条分割线段位置不同,就视为两种不同的剪法.)
剪法一:分割后所得的四个三角形中,![]() ,
,![]() .
.
剪法二:分割后所得的四个三角形中,![]() ,
,![]() .
.
剪法三:分割后所得的四个三角形中,![]() ,
,![]() .
.
 |
6.(本题14分)如图19,点![]() 分别为线段
分别为线段![]() 上的两个动点,且
上的两个动点,且![]() 于点
于点![]() 于点
于点![]() ,若
,若![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
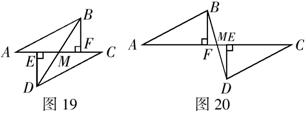 (2)当
(2)当![]() 两点移动至如图20所示的位置时,其余条件不变,上述结论是否成立?若成立,请给予证明.
两点移动至如图20所示的位置时,其余条件不变,上述结论是否成立?若成立,请给予证明.
第24章整章水平测试参考答案
一、1.![]() 2.
2.![]() 3.
3.![]() 4.
4.![]() ;
;![]()
5.![]() 6.
6.![]()
![]() 7.
7.![]() 8.如果两个角是对顶角,那么这两个角相等 9.这两条直线平行 10.
8.如果两个角是对顶角,那么这两个角相等 9.这两条直线平行 10.![]()
二、1~5.BDADD 6~10.BCCBC
三、1.证明:因为![]() (已知),
(已知),
所以![]() .
.
所以![]() (同旁内角互补,两直线平行).
(同旁内角互补,两直线平行).
所以![]() (两直线平行,内错角相等).
(两直线平行,内错角相等).
因为![]() (已知),
(已知),
所以![]() .
.
因为![]() (已知),
(已知),
所以![]() (垂直定义).
(垂直定义).
又因为![]() (公共边),
(公共边),
所以![]() .
.
所以![]() (全等三角形的对应边相等).
(全等三角形的对应边相等).
2.略.
3.当点![]() 为
为![]() 的中点时,
的中点时,![]() .
.
证明:因为![]() (已知),
(已知),
所以![]() (等边对等角).
(等边对等角).
因为![]() (已知),
(已知),
所以![]() (垂直定义).
(垂直定义).
又因为![]() (已知),
(已知),
所以![]() .
.
所以![]() (全等三角形的对应边相等).
(全等三角形的对应边相等).
4.证明:在![]() 上截取一点
上截取一点![]() ,使
,使![]() ,连结
,连结![]() .
.
因为![]() (公共边),
(公共边),![]() (已知),
(已知),
![]() (辅助线的作法),
(辅助线的作法),
所以![]() ,所以
,所以![]() .
.
在![]() 中,
中,![]() ,即
,即![]() ,
,
 所以
所以![]() .
.
5.
(1)![]()
(2)![]()
(3)![]()
6.(1)提示:先证![]() ,得
,得![]() .
.
再证![]() ,得
,得![]() .
.
(2)证明:因为![]() 已知),
已知),
所以![]() 是直角三角形.
是直角三角形.
因为![]() (已知),
(已知),
所以![]() .
.
所以![]() (全等三角形的对应边相等).
(全等三角形的对应边相等).
因为![]() (对顶角相等),
(对顶角相等),![]() ,
,
所以![]() .
.
所以![]() (全等三角形的对应边相等).
(全等三角形的对应边相等).
(3)结论仍然成立,理由:仍然是证(1)中所证的两对三角形全等.