九年级数学第一学期期中检测
试题卷
命题人：鲍凌梅 校对人：王晶晶
一．选择题（每小题3分,共30分）
1．在代数式
, 
, 
, 
, 
, 
中,分式的个数为（
）
A．
个 B．
个 C．
个
D．
个
2．化简
的结果是（ ）
A．
B．
C．
D．
3．如果关于x的方程
是一元二次方程,则k的取值为：（ ）
A.k=0 B.k≠0 C.k=2 D. k≠2
4．一元二次方程
的根的情况是( )
A. 有两个相等的实数根 B.有两个不相等的实数根 C.只有一个实数根
D．没有实数根
5．如图，圆O中圆心角∠AOB=100度，则圆周角∠ACB为（ ）度
A．100度 B．80度 C．50度 D．无法确定
|
|
|
|
|
|
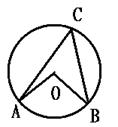
(第5题) (第6题)
6. 如图,在
中,给出以下六个条件:
(1) AB=DE;(2)BC=EF;(3)AC=DF;(4)∠A=∠D;(5)∠B=∠E; (6)∠C=∠F.
以其中的三个作为已知条件,不能 判断这两个三角形全等的是 ( )
A. (1)(2)(5) B. (1)(2)(3) C. (1)(4)(6) D. (2)(3)(4)
7．某商店8月份营业额为10万元,由于加大了广告宣传力度,9月份和10月份的营业额逐月增加.已知10月份的营业额为14.4万元.求该商店后两个月营业额的平均增长率（ ）
A．44％ B．22％ C．20％ D．10％
8.下列说法正确的有 ( )个
①半圆或直径所对的圆周角是直角．②经过三个点一定可以作一个圆．
③圆的切线垂直于经过切点的半径．④垂直于半径的直线是圆的切线；
⑤相等的圆心角所对的弧相等.
Ａ. Ｂ. Ｃ. Ｄ.
9.已知:关于x的一元二次方程
的一个根是
,且二次函数
的对称轴是直线
.则抛物线的顶点坐标是 ( )
A. ( 3 ,-2 ) B. ( 3 ,1 ) C. ( 3 ,2 ) D. ( 2 ,3 )
10．如图,三个半径为3的圆两两外切,且△ABC的每一边都与其中的
两个圆相切,那么△ABC的周长是（ ）
A.
B. 
C. 
D. 
二．填空题（每小题4分,共24分）
11.分式
有意义的条件是 .
12.若关于x的方程
的一个根是1 ,则
13.
用一个半径为8cm的半圆围成一个圆锥的侧面 ,则此圆锥的底面
半径为 
,侧面积为 
.
14.写出一个对称轴在
轴左侧且经过原点的抛物线
的解析式 .
15.如图,过点
、
、
作⊙
,
为
⊙上不同于点、
的一点,则
的度数为 . ( 第15题 )
16. 小强去参加杭州市的数学解题比赛,规定时间为8:30 --
9:40 ,若钟面上的分针长为
,请你计算一下小强在参加整个比赛中,分针在钟面上扫过的面积为_________.
三．解答题：(本题有8个小题,共66分.)
17.解方程(每小题3分,共6分)：
（1）
（2）
18. (本题6分)先化简,再求值：
,其中
．
19. (本题6分)求二次函数
的图象与坐标轴的交点坐标.
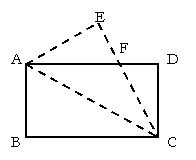
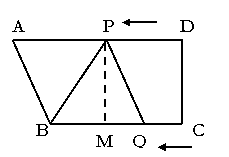
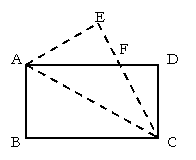
20. (本题8分)如图,将矩形纸片ABCD沿对角线AC折叠,使点B落在E处.求证:EF = DF.
21. (本题8分) 如图:点A是一个半径为500米的圆形森林公园的中心,在森林公园附近有 B、C两个村庄,现要在B、C两个村庄之间修一条长为1200米的笔直公路将两村连通.经测得∠ABC=45°,∠ACB=30°,问此公路是否会穿过森林公园? 请通过计算进行说明.
 |
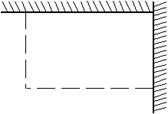
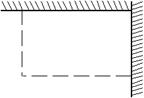
22．(本题10分) 如图,用长为
的篱笆（虚线部分）,两面靠墙围成矩形的苗圃.
（1）设矩形的一边为
,面积为
,求关于
的函数关系式,并写出自变量
的取值范围；
（2）当为何值时,所围苗圃的面积最大,最大面积是多少？
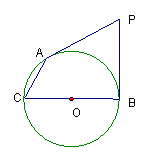
23、(本题10分) 如图从点
向⊙引两条切线
、
,、
是切点,
为弦,
为直径.若
,
, 求:
(1) ∠ACB的度数; (2)的长; (3) 
的长;(4)四边形
的面积.
 |
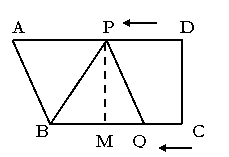
24. (本题12分)如图，在直角梯形ABCD中，AD∥BC，∠C＝90°，BC＝8，DC＝6，AD＝12。动点P从点D出发，沿射线DA的方向以每秒2个单位的速度运动，动点Q从点C出发，在线段CB上以每秒1个单位的速度向点B运动，点P，Q分别从点D，C同时出发，当点Q运动到点B时，点P随之停止运动。设运动的时间为t（秒）。
（1）设△BPQ的面积为S ，求S与t之间的函数关系式.
（2）当t为何值时，∆ BPQ是等腰三角形？
 |
九年级数学第一学期期中检测答题卷
一、选择题：（每小题3分,共30分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题：（每小题4分,共24分）
11. 12. 13. cm , cm2 .
14. 15. . 16. cm2
三、解答题(本题有8个小题,共66分.)
17.解方程(每小题3分,共6分)：
（1）
（2）
18. (本题6分)先化简,再求值：,其中．
19. (本题6分)求二次函数的图象与坐标轴的交点坐标.
20. (本题8分)如图,将矩形纸片ABCD沿对角线AC折叠,使点B落在E处.求证: EF = DF.
21. (本题8分)
22．(本题10分)
 |
23、(本题10分)
24. (本题12分)