九年级（上）数学期中测试卷

九年级（上）数学期中测试卷

姓名____________学号____________得分____________

全卷满分为100分加附加分15分，考试时间90分钟．试卷共5道大题（计27小题）

一、你能填得又快又准吗？

（共10小题，每题3分，共30分）

1.方程x²-4=0的解是 ____________ 。

2.若点（2，1）在双曲线上，则k的值为_______。

3.命题“等腰梯形的对角线相等”。它的逆命题是 　　　　　　　　　　　　 　 。

4.已知一元二次方程有一个根为零，则=　　　。

5.等腰三角形的底角为15°，腰长为20cm，则此三角形的面积为　　　　　　　。

6.请写出一个根为，另一根满足的一元二次方程　　　　　　　　　。

7.小红、小芳、小明在一起做游戏时需要确定作游戏的先后顺序，他们约定用“锤子、剪子、布”的方式确定。请问在一个回合中三个人都出“布”的概率是　　　　 。

8.如图，菱形ABCD的对角线的长分别为2和5，P是对角线AC上任一点（点P不与点A、C重合），且PE∥BC交AB于E，PF∥CD交AD于F，则阴影部分的面积是　　　　 .

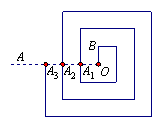
9、如图是一回形图，其回形通道的宽和的长均为1， 回形线与射线　交于…．若从点到点的回形线为第1圈（长为7），从点到点的回形线为第2圈，…，依此类推．则第10圈的长为　　　　 ．

10．如下图，边长为3的正方形ABCD绕点C按顺时针方向旋转30º后得到正方形EFCG，EF交AD于点H，那么DH的长为　　　　　  。

	8题图		9题图

　　　　　　 

二、你一定能选对!（本题共10小题，每题3分，共30分）

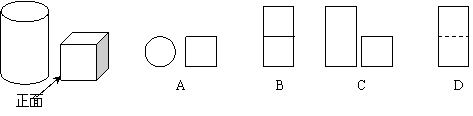
11、小明从正面观察下图所示的两个物体，看到的是　　　　　　　　  （　　）

12．下列四幅图形中，表示两颗小树在同一时刻阳光下的影子的图形可能是(　　)

13. 在一个四边形ABCD中,依次连接各边的中点得到的四边形是菱形, 则对角线AC与BD需要满足条件是 　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　 A.　垂直　 B.　相等　 C.　垂直且相等　 D. 不再需要条件

14．小明用两根同样长的竹棒做对角线，制作四边形的风筝，则该风筝的形状一定是( 　　）

A、矩形　　　B、正方形　　C、等腰梯形　　D、无法确定

15．到三角形各顶点的距离相等的点是三角形　　　　　　　　　　　　　　　 （　　）

A、三边的垂直平分线的交点　　 　 B、三条高的交点　

C、三条角平分线的交点　　　　　　　 D、三条中线的交点

16． 电影院呈阶梯或下坡形状的主要原因是　　　　　　　　　　　　　　　  (　　)

A.为了美观　　  B. 减小盲区 　　 C.增大盲区　　 　 D. 盲区不变

17．学生冬季运动装原来每套的售价是100元，后经连续两次降价，现在的售价是81元，则平均每次降价的百分数是　　　　　　　　　　　　　　　　　　　　　　  (　　)

A、9%　　　　　 B、8.5%　　　　　  C、9.5%　　　　  D、10%

18、在下列四个函数中，随的增大而减小的函数是　　　　　　　　  （　　）

A. 　　B.　　　 C.　　 D.

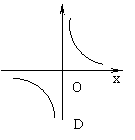
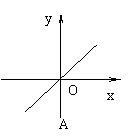
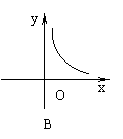
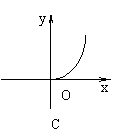19．甲、乙两地相距60km，则汽车由甲地行驶到乙地所用时间y（小时）与行驶速度x（千米/时）之间的函数图像大致是　　　　　　　　　　　　　　　　　 （　　　）

20．元旦节班上数学兴趣小组的同学，互赠新年贺卡，每两个同学都相互赠送一张，小明统计出全组共互送了90张贺年卡，那么数学兴趣小组的人数是多少？设数学兴趣小组人数为x人，则可列方程为　　　　　　　　　　　　　　　　　　　　　　  （　　 ）

A、x(x-1)=90　　　B、x(x-1)=2×90　　 C、x(x-1)=90÷2　　 D、x(x+1)=90

三、作图题。（5分）

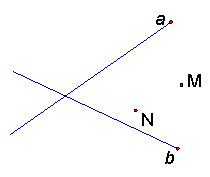
21．a,b分别代表铁路和公路，点M、N分别代表蔬菜和杂货批发市场。现要建中转站O点，使O点到铁路、公路距离相等，且到两市场距离相等。请用尺规画出O点位置，不写作法，保留痕迹。　　

　 

四、解答题。

22、用适当方法解下列方程：（9分）

1、　　　　　 2、　　　 3、

　　

23、(6分) 某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利44元，为了扩大销售，增加盈利，尽快减少库存，商场决定采取适当的降价措施，经调查发现，如果每件衬衫每降价2元，商场平均每天可多售出5件。若商场平均每天要盈利1600元，每件衬衫应降价多少元？

24、（6分）已知：如图，矩形ABCD中，O是AC与ＢＤ的交点，过O点的直EF与AB、CD的延长线分别交于E、F。

1）求证：△BOE≌△DOF

2）当EF与AC满足么条件时，四边形AECF是菱形，并明你的结论。

　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　 F

　　　　　　　　　　　　　　　　　　　　　　A　　　　　　　 D

O

　　　　　　　　　　　　　　　　　　　　　 

　　　　　　　　　　　　　　　　　 

　　　　　　　　　　　　　　　 　　　　　　B　　　　　　　　  C

　　　　　　　　　　　　　　　  　　　　　　E

　

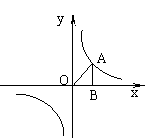
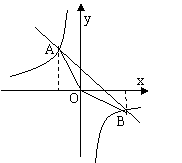
25、(6分) 已知反比例函数与一次函数y=-x+2的图象交于A、B两点，求：　

　(1)A、B两点的坐标；　　(2)△AOB的面积．

　

26、（8分）点P是x轴正半轴上的一个动点，过点P作x轴的垂线PA交双曲线于点A，连结OA.

⑴如图①，当点P在x轴的正方向上运动时，Rt△AOP的面积大小是否变化？若不变，请求出Rt△AOP的面积；若改变，试说明理由.

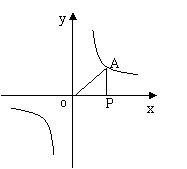
图①

⑵如图②，在x轴上点P的右侧有一点D，过点D作x轴的垂线交双曲线于点B，连结BO交AP于点C.设△AOC的面积为S₁，梯形BCPD的面积为S₂，则S₁与S₂大小关系是

S₁__________S₂(填“>”或“<”或“=”). 试说明理由

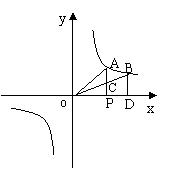
图② 

⑶如图③，AO的延长线与双曲线的另一个交点为点F，FH垂直于x轴，垂足为

点H，连结AH、PF，试证明四边形APFH的面积为常数.

　　　　　　　　　　　　　　　　　　　　　　　　　　 

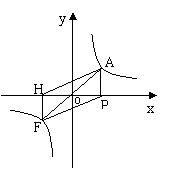
图③

	祝贺你做完了考题,请再仔细检查一遍,看看有没有错的、漏的,别留下什么遗憾哦!

五、附加题：（第1题，每空1分，共2分；第2题2分；第3题3分；第4题，每空2分，共8分；此题共15分）

27、 探索一个问题：“任意给定一个矩形A，是否存在另一个矩形B，它的周长和面积分别是已知矩形周长和面积的一半？”（完成下列空格）

1).当已知矩形A的边长分别为6和1时，小亮同学是这样研究的：设所求矩形的两边分别是，由题意得方程组：

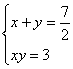，消去y化简得：

∵b²-4ac＝49－48>0　　 ∴　　∴满足要求的矩形B存在.

2).如果已知矩形A的边长分别为2和1，请你仿照小亮的方法研究是否存在满足要求的矩形B.

3).如果矩形A的边长为m和n，请你研究满足什么条件时，矩形B存在？

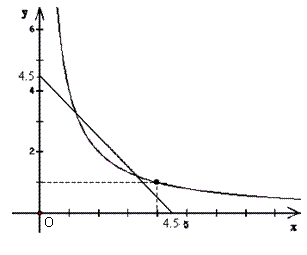
4).如图，在同一平面直角坐标系中画出了一次函数和反比例函数的部分图象，其中x和y

分别表示矩形B的两边长，请你结合刚才的研究，回答下列问题：

①　　 这个图象所研究的矩形A的两边长为___　 __和__　 ___；

②　　 满足条件的矩形B的两边长为___　　 __和___　　　__。

答案

一、填空

1、2或-2　　 2、2　　 3、对角线相等的梯形是等腰梯形　　　 4、-4　　　　 5、100　　　　 6、略　　 7、　　 8、2、5　　　9、79　　　　10、

二、选择题

　　　 C A B D A　　B D B B A

三、略

四、解答题

22、（1）5+　 5-　 （2）2　 -　　（3）1　

23、每件衬衫降价12或24 元。

24、略

25、A（-2、4）　B（4、-2 ）　　　　S=6

26、（1）S=　　（2）=　　　 （3）2

五、附加题

1、或2　　2、不存在　　3、当+≥6mn时 ，矩形存在

4、 A：8，1　 B：，