九年级数学试卷
班级_________姓名_________学号_________
参考公式：二次函数y=ax2+bx+c的顶点坐标是
一. 选择题（本题共10小题，每小题4分，共40分，请选出各题中一个符合题意的正确选项，不选、多选、错选均不给分）
1、反比例函数
的图像经过点（1，－3），则k的值为（ ）
A、－3 B、3 C、
D、－
2、抛物线
的顶点坐标为
（ ）
A．（2 ，5） B．（-5 ，2） C．（5 ，2） D．（-5 ，-2）
3、如图，A，B，C是⊙O上的三点，∠BAC= 44°，则∠BOC的大小是( )
A．22° B．44° C．66° D．88°
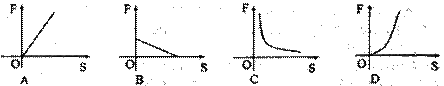4、已知力F所作的功是10焦，则力F与物体在力的方向通过的距离S之间关系的图象大致是 ( )
5、二次函数
的图象向右平移4个单位，得到新的图象的函数表达式是( )
(A)
(B)
(C)
(D)
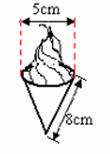
6、如图，冰淇淋蛋筒下部呈圆锥形，则蛋筒圆锥部分包装纸的面积（接缝忽略不计）（ ）
A．20
B．40
C．20
D．40
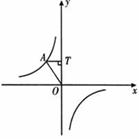
7、如图，点A是反比例函数图象上的一点，自点A向y轴作垂线，垂足为T，已知
S△AOT＝4，则此函数的表达式为 （ ）
A．
B．
C．
D．
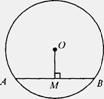
8、如图，⊙O的半径为5，圆心O到弦AB的距离OM的长为3，则弦AB的长是（ ）
A、4 B、6 C、7 D、8
9、根据下列表格的对应值：
| x | 3.23 | 3.24 | 3.25 | 3.26 |
|
| －0.06 | 0.02 | 0.05 | 0.09 |
判断方程
(a≠0，a，b，c为常数)一个解x的范围是（ ）
A、3＜x＜3.23 B、3.23＜x＜3.24
C、3.24＜x＜3.25 D、3.25 ＜x＜3.26
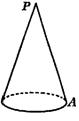
10、.如图，底面半径为1，母线长为4的圆锥，一只小蚂蚁若从A点出 发，绕侧面一周又回到A点，它爬行的最短路线长是（ ）
二、填空题（本题有6小题，每小题5分，共30分）
11、试写出图象位于第二象限与第四象限的一个反比例函数解析式 .
12、钟表的轴心到分针针端的长为6cm，那么经过40分钟，分针针端转过的弧长是_______ cm(用π表示) .
13、如图，抛物线对称轴是x=1，与x轴交于A、B两点，若B点坐标是(
，0)，则A点的坐标是____.
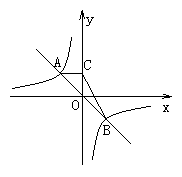14、如图, 如果函数y=－x与y=
的图像交于A、B两点, 过点A作AC垂直于y轴, 垂足为点C, 则△ABC的面积为______.
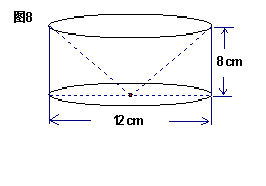
15、如图8，这是一个由圆柱体材料加工而成的零件，它是以圆柱体的上底面为底面，在其内部“掏取”一个与圆柱体等高的圆锥体而得到的，其底面直径AB =
，高BC =
，求这个零件的表面积是__________；（结果保留）
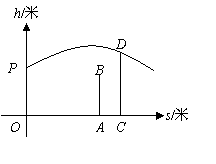16、甲、乙两人进行羽毛球比赛，甲发出一颗十分关键的球，出手点为
，羽毛球飞行的水平距离
（米）与其距地面高度
（米）之间的关系式为
．如图，已知球网
距原点5米，乙（用线段
表示）扣球的最大高度为
米，设乙的起跳点
的横坐标为
，若乙原地起跳，因球的高度高于乙扣球的最大高度而导致接球失败，则的取值范围是 ．
三、解答题（本题有8小题，第17～20题每题8分，第21题10分，第22、23题每题12分，第24题14分，共80分）
17、小明发现把一双筷子摆在一个盘子上，可构成多种不同的轴对称图形，请你按下列要求，各添画一只筷子，完成其中三种图形：
 |
18、某气球内充满了一定质量的气球,当温度不变时,气球内气球的压力p(千帕)是气球的体积V(米2)的反比例函数,其图象如图所示(千帕是一种压强单位)
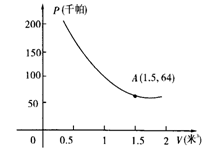（1）写出这个函数的解析式；
（2）当气球的体积为0.8立方米时,气球内的气压是多少千帕？
（3）当气球内的气压大于144千帕时,气球将爆炸,为了安全起见,气球的体积应不小于多少立方米？
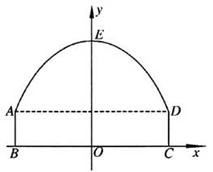19、如图，隧道的截面由抛物线AED和矩形ABCD构成，矩形的长BC为8m，宽AB为2m，以BC所在的直线为x轴，线段BC的中垂线为y轴，建立平面直角坐标系。y轴是抛物线的对称轴，顶点E到坐标原点O的距离为6m。
（1）求抛物线的解析式；
（2）如果该隧道内设双行道，现有一辆货运卡车高5m，宽2米，这辆货运卡车能否通过该隧道？通过计算说明你的结论。
20、图1是某学校存放学生自行车的车棚的示意图（尺寸如图所示），车棚顶部是圆柱侧面的一部分，其展开图是矩形．图2是车棚顶部截面的示意图，
所在圆的圆心为O．
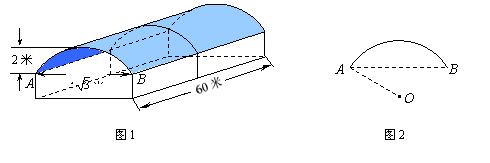车棚顶部是用一种帆布覆盖的，求覆盖棚顶的帆布的面积（不考虑接缝等因素，计算结果保留
）．
21如图，已知反比例函数
的图象经过点
，一次函数
的图象经过点
与点
，且与反比例函数的图象相交于另一点
．
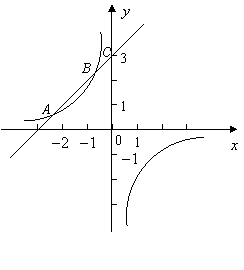（1）分别求出反比例函数与一次函数的解析式；
（2）求点的坐标．
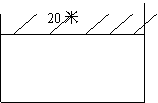22、农民李大伯为了致富奔小康，大力发展家庭养殖业，他准备用30米长的木栏围一个矩形的羊圈，为了节约材料，同时要使矩形面积最大，他利用了自己家房屋一面长20米的墙，设计了如图一个矩形的羊圈。
（1）请你求出张大伯设计的矩形羊圈的面积。
（2）请你判断他的设计方案是否使矩形羊圈的面积最大？如果不是最大，应怎样设计？请说明理由。
23、如图，点
在圆上，弦
的延长线与弦
的延长线相交于点．
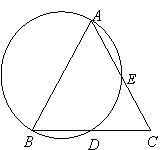给出下列三个条件：
①是圆的直径；
②
是
的中点；
③
．
请在上述条件中选取两个作为已知条件，第三个作
为结论，写出一个你认为正确的命题，并加以证明．
条件： ．
结论： ．
证明：
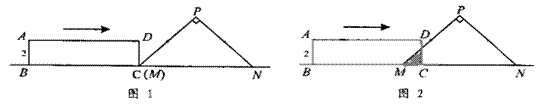
24、如图，Rt△PMN中，∠P＝90°，PM＝PN，MN＝8cm，矩形ABCD的长和宽分别为8cm和2cm，C点和M点重合，BC和MN在一条直线上。令Rt△PMN不动，矩形ABCD沿MN所在直线向右以每秒1cm的速度移动（如图2），直到C点与N点重合为止。设移动x秒后，矩形ABCD与△PMN重叠部分的面积为y
。求y与x之间的函数关系式。
