九年级(下)数学单元测试卷6
第一章 证明(二)
班级 姓名 得分
一、选择题(每小题3分，共30分)
1、满足下列条件的两个三角形一定全等的是（ ）
A、腰相等的两个等腰三角形 B、一个角对应相等的两个等腰三角形
C、斜边对应相等的两个直角三角形 D、底相等的两个等腰直角三角形
2、如图，在Rt△ABC中，∠ACB=90°，AC=2BC，在直线BC或AC上取一点P，使得△PAB为等腰三角形，则符合条件的点P共有（ ）
A、4个 B、5个 C、6个 D、7个
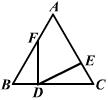
3、如图，△ABC中，AB=AC，D、E、F分别是BC、AC、AB上的点，，且BF=CD，BD=CE，则∠EDF=（ ）
A、90°–∠A B、90°–
∠A C、180°–∠A D、45°–∠A
4、等腰三角形底边上的高与底边的比是1∶2，则它的顶角等于（ ）
A、90° B、60° C、120° D、150°
5、等腰三角形顶角为100°，两腰垂直平分线相交于点P，则（ ）
A、点P在三角形内 B、点P在三角形底边上
C、点P在三角形外 D、点P的位置与三角形的边长有关
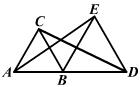
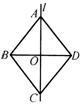
6、如图，△ABC与△BDE都是等边三角形，AB<BD。若△ABC不动，将△BDE绕B点旋转，则在旋转过程中，AE与CD的大小关系为（ ）
A、AE=CD B、AE>CD C、AE<CD D、无法确定
7、在△ABC中，∠A∶∠B∶∠C=1∶2∶3，则BC∶AC∶AB=（ ）
A、1∶2∶3 B、1∶4∶9 C、1∶
∶
D、1∶∶2
 | |||||||
 | |||||||
 | |||||||
 | |||||||
(第2题图) (第3题图) (第6题图) (第8题图)
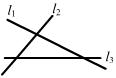
8、如图，l1、l2、l3表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可选择的地址有（ ）
A、一处 B、二处 C、三处 D、四处
9、△ABC中，∠C=90°，AB的垂直平分线交AB于E，交BC于点D，若CD∶BD=1∶2，BC=6cm，则点D到点A的距离为（ ）
A.1.5cm B.3cm C.2cm D.4cm
10、直角三角形的周长为2+
，斜边上的中线为1，则该三角形的面积等于（ ）
A、1 B、
C、
D、
二、填空题(每小题3分，共18分)
11、如图，已知AC=BD，∠A=D=90°，要使得△ABC≌△DCB，只需增加的一个条件是___________(填一个你认为正确的条件即可).
12、等腰三角形一腰上的高与另一腰的夹角为30°，腰长为a，则其底边上的高是 .
13、直角三角形斜边上的高与中线分别是5cm和6cm，则它的面积是 cm2.
 |  | ||||
 | |||||
(第11题图) (第17题图) (第18题图)
14、如果一个三角形的一条角平分线恰好是对边上的高，那么这个三角形是 三角形.
15、如果两个等腰三角形 ，那么这两个等腰三角形全等(只填一种能使结论成立的条件即可).
16、在△ABC中，∠A=50°，AB=AC，AB的垂直平分线DE交AC于D，则∠DBC的度数是______________。
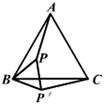
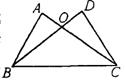
17、如图所示，P是等边三角形ABC内一点，将△ABP绕点B顺时针方向旋转60°，得到△CBP′，若PB=3，则PP′= 。
18、如图，l是四边形ABCD的对称轴，如果AD∥BC，有下列结论：①AB∥CD； ②AB＝BC ；③AB⊥BC ；④AO＝OC。其中正确的结论是______________________________．（把你认为正确的结论的序号都填上）
三、(每小题6分，共12分)
19、已知：线段a、h(如图)
求作：△ABC，使AB=AC，且BC=a，高AD=h.
请你用尺规作图，并补全作法
作法：(1)作线段BC= .
(2)作 .
(3) .
(4)连结 .
则△ABC为所求等腰三角形.
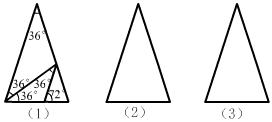
20、如图，△ABC中，AB=AC，∠A=36°.仿照图(1),请你设计两种不同的分法，将△ABC分割成3个三角形，使每个三角形都是等腰三角形(要求标出每个等腰三角形三个内角的度数).
 |
四、(每小题6分，共18分)
21、已知：如图，△ABC中，AB=AC，∠A=120°.
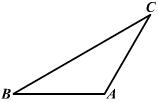(1)用直尺和圆规作AB的垂直平分线，分别交BC、AB于点M、N(保留作图痕迹，不写作法).
(2)猜想CM与BM之间有何数量关系，并证明你的猜想。
22、已知：如图，CE⊥AB，BF⊥AC，CE与BF相交于D，且BD=CD.
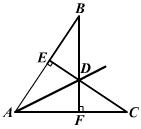求证：D在∠BAC的平分线上.
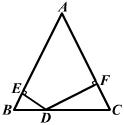23、已知：如图，D是等腰ABC底边BC上一点，它到两腰AB、AC的距离分别为DE、DF，当D点在什么位置时，DE=DF？并加以证明.
五、(每小题8分，共16分)
24、为美化环境，计划在某小区内用30平方米的草皮铺设一个边长为10米的等腰三角形绿地，请你求出这块等腰三角形绿地另两边的长。
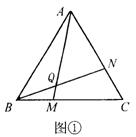
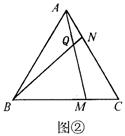
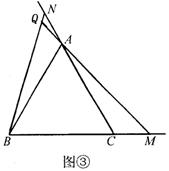
25、已知△ABC为正三角形，点M是射线BC上任意一点，点N是射线CA上任意一点，且BM＝CN，直线BN与AM相交于Q点．就下面给出的三种情况（如图①、②、③），先用量角器分别测量∠BQM的大小，然后猜测∠BQM等于多少度？并利用图③证明你的结论．
