反比例函数

第一学期九年级单元测试题

《反比例函数》

班级：　　　　   姓名：　　　　　  座号：　　　　  得分：　　　　

（说明：考试时间为120分钟，总分100分）

一．　  填空题（每空2分，共30分）

1．如果函数是反比例函数，那么k=________，此函数的解析式是____　 ___　　　 。

2．已知反比例函数，当时，其图象的两个分支在第一、三象限内；当时，其图象在每个象限内随的增大而增大；

3、已知反比例函数图象与直线和的图象过同一点，则当＞0时，这个反比例函数值随的增大而　　　　 （填增大或减小）；

4、已知函数，当时，，则函数的解析式是　　　　　　 ；

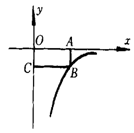
5、如图，面积为3的矩形OABC的一个顶点B在反比例函数的图象上，另

三点在坐标轴上，则=　　　　　　.

6、反比例函数与一次函数的图象有一个交点是（-2，1），则

它们的另一个交点的坐标是　　　　　　 .

7．若点A(7，)、B(5，)在双曲线上，则和的大小关系为_________；

8．如果与成反比例，z与成正比例，则z与成____　　　　 ______；

9． 若反比例函数的图象位于一、三象限内，正比例函数过二、四象限，则的整

数值是________；

10．若直线和双曲线在同一坐标系内的图象无交点，则 、的关系是

_________；

11、已知函数的图象有两个交点，其中一个交点的横坐标为1，则两个函数图象的交点坐

标是　　　　　 ；

12．反比例函数的图象经过点P（，），且、b为是一元二次方程的两根，那么

点P的坐标是________　　　_，到原点的距离为_________；

13、在函数（为常数）的图象上有三个点（-2，），(-1，)，（，），函数值，，

的大小为　　　　　　 ；

二．选择题：（每小题3分，共21分）

1、下列函数中，是反比例函数的为（　　 ）

（A）　　（B）　（C） （D）　

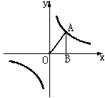
2．如图，A为反比例函数图象上一点，AB轴与点B，若，

则为（　　）

A 、　　  B、　　　　C、 　　 D、无法确定

3．函数的图象经过（，，则函数的图象是（　　）

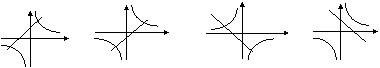4．在同一坐标系中，函数和的图像大致是（　　）

A　　　　　　　 B　　　　　　　　 C　　　　　  D　

5．已知反比例函数的图像上有两点A(，)，B(，)，且，则的值是（　　）

　 A　 正数　　B　负数　　 C　非正数　　 D　不能确定

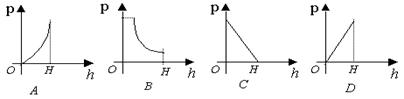
6、已知圆柱的侧面积是100cm²，若圆柱底面半径为r（cm²），高线长为h（cm），则h关于r的函数的图象

大致是（　　 ）　　　　　　　　　　　　　 

 

7．已知反比例函数的图像经过点（，），则它的图像一定也经过（　　）

A (－,－)　　B (,－)　 C (－，)　D （0，0）

二、解答题：（最后一题9分，其余每小题8分，共49分）

1、　　　已知：反比例函数和一次函数，其中一次函数的图像经过点（，5）.

（1）  试求反比例函数的解析式；

（2）　　　 若点A在第一象限，且同时在上述两函数的图像上，求A点的坐标；

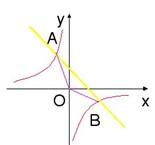2．如图，已知一次函数的图象与反比例函数的图象交于A，B两点，且A点的横坐标与B点的纵坐标都是；

（1）　　　 一次函数的解析式

（2）　　　 △AOB的面积。

3．点A是双曲线与直线在第二象限的交点，AB垂直轴于点B，且S_△ABO=；

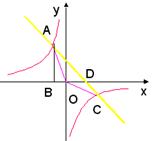（1）求两个函数的表达式

（2）求直线与双曲线的交点坐标和△AOC的面积。

4、已知反比例函数和一次函数的图象都经过点，

⑴ 求点P的坐标和这个一次函数的解析式；

⑵ 若点M(，)和点N (，)都在这个一次函数的图象上．试通过计算或利用一次函数的性质，说明大于

5、已知与成反比例，与成正比例，并且当=3时，=5，当=1时，=-1；求与之间的函数关系式.

6．已知□ABCD中，AB = 4，AD = 2，E是AB边上的一动点，设AE=，DE延长线交CB的延长线于F，设CF =，求与之间的函数关系。