方程与不等式中考题

方程与不等式中考题

1．(2006年浙江省绍兴市)不等式2-x>1的解集是　A．z>1　　B．x<1　C．z>-1　　D．z<-1

2．(06年重庆市)不等式组的解集是（）A.　B. C. D.无解

3．（2006年大连市）今年4月某天的最高气温为8℃，最低气温为2℃，则这天气温t℃的t的取值范围是________________。

4．（2006年大连市）已知关于x的方程x²＋kx－2＝0的一个解与方程解相同。

（1）求k的值；（2）求方程x²＋kx－2＝0的另一个解。

5．（江西省）小杰到学校食堂买饭，看到A、B两窗口前面排队的人一样多（设为a人，a>8），就站在A窗口队伍的后面，过了2分钟，他发现A窗口每分钟有4人买了饭离开队伍上，B窗口每分钟有6人买了饭离开队伍，且B窗口队伍后面每分钟增加5人。

（1）此时，若小杰继续在A窗口排队，则他到达窗口所花的时间是多少（用含a的代数式表示）？　　　

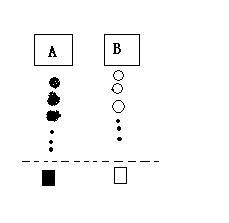（2）此时，若小杰迅速从A窗口队伍转移到B窗口后面重新排队，且到达B窗口所花的时间比继续在A窗口排队到达A窗口所花的时间少，求a的取值范围（不考虑其它因素）。

6．（江西省）已知关于x的一元二次方程x+kx-1=0 ,(1)求证：方程有两个不相等的实数根；　（2）设方程的两根分别为x,x,且满足x＋x＝x·x，求k的值。

7．（江西省）某公司2003年缴税60万元，2005年缴税80万元，设该公司这两年缴税的年平均增长率为x,则得到方程（　　　　　）

A、60＋2x=80　 B、60（x＋1）＝80　　C、60x＝80　　D、60(x+1)=80

8．（江西省）方程的解是_______________________。

9．（2006年长春市）A城市每立方米水的水费是B城市的1.25倍，同样交水费20元，在B城市比在A城市可多用2立方米水，那么A、B两城市每立方米水的水费各是多少元？

设B城市每立方米水的水费为x元，则A城市为1.25x元，　　

解得x = 2。　 经检验x = 2是原方程的解。 1.25x = 2.5（元）。　　　答：B城市每立方米水费2元，A城市每立方米2.5元。

10．（2006年长春市）不等式组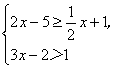的解集是_____________________。x≥4

11．（2006年海淀区）解不等式组：

　　　 解： ，　　　由<1>解得：，　由<2>解得：

　　　 因此原不等式组的解集为。

12．（2006年海淀区）解分式方程：

　　　 解：去分母得：，去括号得：，　　解得：，　　经检验是原方程的解。　　　 所以原方程的解为。

13．（2006年海淀区）已知下列n（n为正整数）个关于x的一元二次方程：

　　　

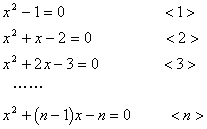
　　　 （1）请解上述一元二次方程<1>、<2>、<3>、<n>；

　　　 （2）请你指出这n个方程的根具有什么共同特点，写出一条即可。

　　　 解：（1）<1>，所以

　　　 <2>，所以

　　　 <3>，所以

　　　　　　　……

　　　 <n>，所以

　　　 （2）比如：共同特点是：都有一个根为1；都有一个根为负整数；两个根都是整数根等。

14．（2006年旅顺口区）　　　　　　

根据对话的内容，试求出饼干和牛奶的标价各是多少元？

解：设饼干的标价每盒x元，牛奶的标价为每袋y元， 则

　　 　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

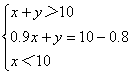
由②得y=9.2－0.9x 　④　把④代入①，得x+9.2－0.9x＞10 ∴　x ＞8　　由③得8＜x＜10 　　　∵x是整数　　∴x=9　将 x=9代入④，得　y=9.2－0.9×9=1.1　答 ：饼干一盒标价9元，一袋牛奶标价1.1元．

15．（2006年旅顺口区）已知关于x的方程的一个解与方程的解相同．⑴求k的值；⑵求方程的另一个解.

解：（1）∵　　∴ ∴ 经检验是原方程的解，把代入方程解得k=3。

（2）解，得，x₂=1∴方程的另一个解为x=1

16．（2006年贵阳市）某汽车租赁公司要购买轿车和面包车共10辆，其中轿车至少要购买3辆，轿车每辆7万元，面包车每辆4万元，公司可投入的购车款不超过55万元；

（1）符合公司要求的购买方案有几种？请说明理由；（8分）

（2）如果每辆轿车的日租金为200元，每辆面包车的日租金为110元，假设新购买的这10辆车每日都可租出，要使这10辆车的日租金不低于1500元，那么应选择以上那种购买方案？

 （1）设轿车要购买辆，那么面包车要购买辆，由题意得：，解得： ，又∵，则。∴购机方案有三种：方案一：轿车3辆，面包车7辆；方案二：轿车4辆，面包车6辆；方案三：轿车5辆，面包车5辆。

　　 （2）方案一的日租金为：（元）；方案二的日租金为：（元）；方案三的日租金为：（元）。为保证日租金不低于1500元，应选择方案三。

17．（2006年贵阳市）甲乙两人加工同一种玩具，甲加工90个玩具所用的时间与乙加工120个玩具所用的时间相等，已知甲乙两人每天共加工35个玩具，求甲乙两人每天各加工多少个玩具？

解：设每天加工个玩具，那么乙每天加工（）个玩具，由题意得：　　　 ，解得：，经检验：是原方程的根，。答：甲每天加工15个玩具，乙每天加工20个玩具。

18．（2006年贵阳市））已知二元一次方程：（1）；（2）；（3）；

请从这三个方程中选择你喜欢的两个方程，组成一个方程组，并求出这方程组的解；

选择（1）和（2）组成方程组（其它组合情况可参照本解法评分）

，（1）+（2）得：，，把代入（1）得：∴原方程组的解是。注：（1）和（3）组成的方程组的解是，（2）和（3）组成的方程组的解是。

19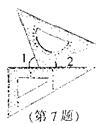．（2006年江西省南昌市）一副三角扳按如图方式摆放，且∠1的度数比∠2的度数大50°，若设∠1=x°∠2=y°，则可得到方程组为　　【　】D

 A B C D

20．（2006年江西省南昌市）已知关于x的一元二次方程

　　(I)求证方程有两个不相等的实数根：

(2)设的方程有两根分别为日满足 求k的值。

(1)证明：∵△=，∴原方程有两个不相等的实数根

  (2)解：由根与系数的关系，得   ，，解得k=1

21．（2006年南安市）解方程：x²—1 =0．解：x=1∴x=1,x=-1

22．(2006年泰州市)若关于的一元一次方程的解是,则的值是B

A． 　　　　　　B．1　　　　　　  C．　　　 　 D．0

23．(2006年苏州市)我国《劳动法》对劳动者的加班工资作出了明确规定．“五一”长假期间．前3天是法定休假日，用人单位应按照不低于劳动者本人日工资或小时工资的300％支付加班工资．后4天是休息日，用人单位应首先安排劳动者补休，不能安排补休的，按照不低于劳动者本人日工资或小时工资的200％支付加班工资．小朱由于工作需要，今年5月2日、3日、4日共加班三天，已知小朱的日工资标准为47元，则小朱“五一”长假加班三天的加班工资应不低于＿＿＿＿＿＿＿＿元。376；

24．(2006年苏州市)解方程：

原方程可化为，解得，经检验，原方程的解为

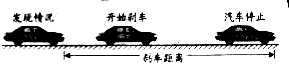
25．(2006年苏州市)　司机在驾驶汽车时，发现紧急情况到踩下刹车需要一段时间，这段时间叫反应时间．之后还会继续行驶一段距离．我们把司机从发现紧急情况到汽车停止所行驶的这段距离叫“刹车距离”(如图)．已知汽车的刹车距离s(单位：m)与车速v(单位：m／s)之同有如下关系：s=tv+kv²其中t为司机的反应时间(单位：s)，k为制动系数．某机构为测试司机饮酒后刹车距离的变化，对某种型号的汽车进行了“醉汉”驾车测试，已知该型号汽车的制动系数k=0.08，并测得志愿者在未饮酒时的反应时间t=O.7s

　　(1)若志愿者未饮酒，且车速为11m／s，则该汽车的刹车距离为＿＿＿＿m(精确到0.1m)

　　(2)当志愿者在喝下一瓶啤酒半小时后，以17m／s的速度驾车行驶，测得刹车距离为

46m．假如该志愿者当初是以11m／s的车速行驶，则刹车距离将比未饮酒时增加多少？(精确到O.1m)

　　(3)假如你以后驾驶该型号的汽车以11m／s至17m／s的速度行驶，且与前方车辆的车距保持在40m至50m之间．若发现前方车辆突然停止，为防止“追尾”。则你的反应时间应不超过多少秒?(精确到0. O1s)　

解：(1)17.4m；(2)设志愿者饮酒后的反应时间为t₁,则t₁×17+0.08×17²=46，t_l≈1.35 s．

当v=11m／s时，s= t_l ×11+0.08×11²=24.53．∴24.53一17.38≈7．2(m)。答：刹车距离将比未饮酒时增加7.2m；(3)为防止“追尾”当车速为17 m／s时，刹车距离必须小于40m,

∴^t×17+0.08×17²<40解得t＜0.993（s）。答：反应时间不超过0.99s

26．（06年连云港市）关于x的一元二次方程x²＋kx－1=0的根的情况是

A、有两个不相等的同号实数根　　 B、有两个不相等的异号实数根

C、有两个相等的实数根　　 　　　D、没有实数根

27．

28．

29．

30．

31．