2版
九年级上第二十七章《相似三角形》第一期随堂
练习及快乐周周练
随堂练习一
一、练习内容：图形的相似
二、练习目标：
1.了解相似图形的定义及日常生活中常见的相似形；
2.掌握相似多边形的性质，并运用它进行计算；
3.在学习相似多边形的定义和性质时，要充分运用理论联系实际的思想.
三、练习题
（一） 仔细看，选一选
1．下列图形一定是相似多边形的是（ ）
A 任意两个矩形 B 任意两个菱形
C 任意两个正方形 D 任意两个平行四边形
2．语句：“①所有度数相等的角都相似；②所有边长相等的菱形都相似；③所有的正方形都相似；④所有的圆都相似”中准确的有( ).
(A)4句 (B)3句 (C)2句 (D)1句
3.小明用如图所示的胶滚沿从左到右的方向将图案滚涂到墙上,如图 所示给出的四个图案中,符合图示胶滚图案的是( )
(二） 耐心想，填一填
4．相距1000km的两市在比例尺为1:的地图上的距离约是___cm (精确到0.1)；某市规划筹建一个开发区，这个开发区在1:50000的地图上面积是30cm2,实际占地面积约为_______________km2
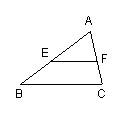
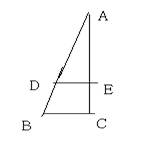
5．如图EF//BC，已知AE=4 BE=3 则AE：AB=_______ EF：BC=______
6.一个多边形的边长分别是2、3、4、5、6，另一个和它相似的多边形的最短边长为6，则这个多边形的最长边为________.
(三) 动手做，解一解
7.一块长3米，宽1.5米的矩形黑板，镶在其外围的木质边框宽7.5厘米，边框里外边缘所成的矩形相似吗？为什么？
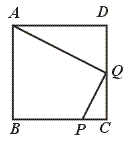
8.一个直立的油桶高0.8米，在顶部的一个开口中将一根长1米的木杆斜着插入桶内，上端正好与桶面相平，抽出后看到杆上油浸到部分长0.8米，求油桶内油面的高度.
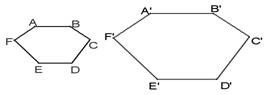
9.如下图两个正六边形ABCDEF与A,B,C,D,E,F,相似，已知AB=5cm EF=6cm,CD与C,D,的比值为1:3,∠E=1250,求A,B,,C,D,的长及∠E,的度数.
参考答案
一、选择题
1. C 2.B 3.C
二、填空题
4.①3.3②7.5 5. 均是4:7 6.18
三、解答题
7. 不相似，因为对应边不成比例。 8.0.64米
9.A,B,=15cm E,F,=18cm ∠E,=1250
随堂练习二
一、练习内容：相似三角形的判定.
二、练习目标：
1.进一步理解相似三角形的定义.
2.要掌握相似三角形的四个判定定理并熟练的运用它来做题.
3在学习相似三角形的四个判定定理时,要灵活运用类比的思想方法.
三、练习题
(一) 仔细看，选一选
1. 下列判断中，正确的是（ ）
（A）各有一个角是67°的两个等腰三角形相似
（B）邻边之比都为2︰1的两个等腰三角形相似
（C）各有一个角是45°的两个等腰三角形相似
（D）邻边之比都为2︰3的两个等腰三角形相似
2.在Rt△ABC中，CD是斜边AB上的高，则图中的相似三角形共有（ ）
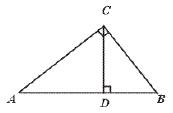
（A）1对 （B）2对 （C）3对 （D）4对
3.下列语句中不正确的是( ).
(A)求两条线段的比值，必需采用相同的长度单位
(B)求两条线段的比值，只需采用相同的长度单位，与选用何种长度单位无关
(C)两个相似三角形中，任意两组边对应成比例
(D)不相似的两个三角形中，也有可能两组边对应成比例
4．在⊿ABC和⊿A,B,C,由下列条件能判断两三角形相似的有：（ ）
（1）∠A=∠A，=700，AB=9，AC=15，A，B,=15,A,C,=20
（2）∠A=600,∠B=380,∠A,=600,∠B=820
（3）AB=1.5,BC=1.2,AC=1.8,A,B,=42,B,C,=35,C,A,=28
A. 0个 B. 1个 C. 2个 D. 3个
5.如图,下列各式能使△ACB∽△DCA的是( )
A 
B 
C 
D 
(二) 耐心想，填一填
6．D、E分别在△ABC的边AB、AC上，要使△AED∽△ABC，应添上下列条件中的任意一个：______________ (要求写出不少于三个条件)
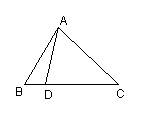
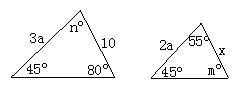
7.如图所示的两个三角形是相似的,则x=_____,m=_____,n=_______.
(三）动手做，解一解
8. 已知：AB⊥BC于B，CD⊥BC于C，AB=4，CD=6，BC=15，P为BC上一点，试问BP为何值时，△ABP与以P、C、D为顶点的三角形相似。
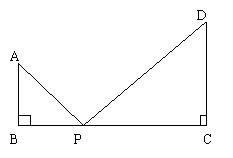
9.已知：如图，AB·BF=BD·BC，求证：⊿AFE∽⊿DCE
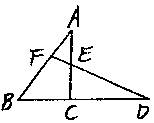
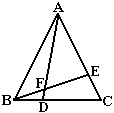
10.如图示：⊿ABD≌⊿AEC，求证：⊿ADE∽⊿ABC。
参考答案
一、选择题
1. B 2.C 3.C 4.C 5.B
二、填空题
6.∠ADE=∠C或∠AED=∠B或AD：AE=AC：AB 7. 
，800，550，
三、解答题
8．6或9， 9.由已知可证⊿ABC∽⊿DFB，得∠A=∠D再利用对顶角相等可证。
10. 由已知可得：∠BAD=∠CAE，AB=AC，AD=AE，再证∠BAC=∠DAE，AB与AD及AC与AE的比值相等。
随堂练习三
一、练习内容：相似三角形应用举例
二、练习目标：
1.充分掌握相似三角形的判定定理和相似三角形的性质定理。
2.会借助相似三角形的判定和性质定理解答实际生活中的几何问题.
3.要理解有关相似形的有关实际生活中常见的相似形题目，并能把它转换成几何图形题；
4.要充分运用理论联系实际的思想.
三、练习题
（一） 仔细看，选一选
1.如图,AB是斜靠在墙上的长梯,梯脚B距墙脚C有1.6m,梯上点D距墙1.4m,BD长0.55m,则梯子的长AB为( )
A.3.85m B.4.00m C.4.40m D.4.50m
（1题图）
2.一个钢筋三角架三边长分别为20cm,50cm,60cm,现要再做一个与其相似的钢筋三角架,而只有长为30cm和50cm的两根钢筋,要求以其中的一根为一边,从另一根截下两段(允许有余料)作为另两边,则不同的截法有( )
A.一种 B.两种 C.三种 D.四种
3.我们已经学习和掌握了不少在平地上测量建筑物高度的方法，如果在同一个斜坡上，在同一时刻,测得在斜坡上自己的影子和一幢大楼的影子长，那么由自己的身高( ).
(A)也能够求出楼高
(B)还须知道斜坡的角度，才能求出楼高
(C)不能求出楼高
(D)只有在光线垂直于斜坡时，才能求出楼高
4.相邻两根电杆AB、CD都用钢索在地面上固定，如图，一根电杆钢索（AB）系在离地面4米处，另一根电杆钢索（CD）系在离地面6米处，则中间两根钢索相交处点P离地面( ).
(A)2.4米 (B)2.8米
(C)3米 (D)高度不能确定
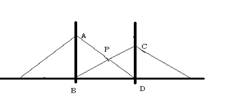
(4题图)
(二） 耐心想，填一填
5．雨后初晴，一学生在运动场上玩耍，从他前面2m远一块小积水处，他看到了旗杆顶端的倒影，如果旗杆底端到积水处的距离为40m，该生的眼部高度是1.5m，那么旗杆的高度是______m．
6.如图，测量小玻璃管口径的量是ABC上，AB的长为10毫米，AC被分为60等份，如果小管口DE正好对着量具上30份处（DE∥AB），那么小管口径DE的长是______毫米．
(三) 动手做，解一解
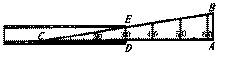
7.一位同学要测一建筑物高，身边未带任何工具，但知道自己的身高为1.65米，鞋长为0.27米。
（1）如何通过影子的度量达到目的？（可用文字、草图以及字母符号辅助说明）
（2）若建筑物的影子长为55米，自己的影子长为1.1米，此建筑物大约有多高？
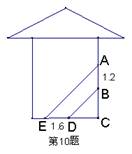
8.如图，阳光通过窗口照到室内，在地面上留下1.6m宽的亮区DE，已知亮区一边到窗下的墙脚距离CE=3.6m，窗高AB=1.2m，那么窗口底边离地面的高度BC是多少米？
参考答案
一、选择题
1. C 2.B 3.A 4.A
二、填空题
5. 30 6. 5
三、解答题
7.①记下同一时刻自己和建筑物影子的位置，然后用脚度量出自己和建筑物影子的大致长度，利用同一时刻自己及建筑物实际高度和影子的长成比例可求出建筑物的高。 ② 82.5米
8．1.5米
3版
快乐周周练二
[每周必读]
本周主要学习了相似多边形的性质，相似三角形的判定和性质以及应用。重点学习了相似三角形的判定和性质，希望同学们要掌握好这些，为以后的学习奠定基础。
(一)仔细看，选一选（每小题3分,共24分）
1..下列语句正确的是( )
A.在 △ABC和△A′B′C′中,∠B=∠B′=90°,∠A=30°,
∠C′=60°, 则⊿ABC和⊿A′B′C′不相似;
B.在⊿ABC和⊿A′B′C′中,AB=5,BC=7,AC=8,A′C′=16,
B′C′=14,A′B ′=10,则⊿ABC∽⊿A′B′C′;
C.两个全等三角形不一定相似;
D.所有的菱形都相似
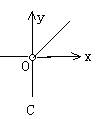
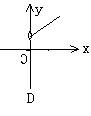
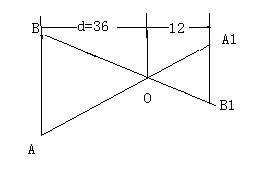
2.根据图中尺寸（AB∥A1B1）,那么物象长（A1B1的长）与物长（AB的长）之间函数关系的图像大致是（ ）
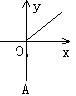
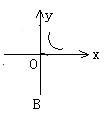
3.如图，在正三角形ABC中，D、E分别在AC、AB上，且
＝
，AE＝BE，则有（ ）
（A）△AED∽△BED （B）△AED∽△CBD
（C）△AED∽△ABD （D）△BAD∽△BCD
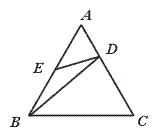
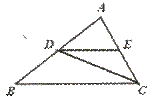
( 3题 ) (4题)
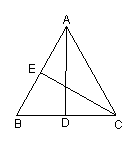
4．已知：如图，∠ADE＝∠ACD＝∠ABC，图中相似三角形共有（ ）
（A）1对 （B）2对 （C）3对 （D）4对
5.三角形三边之比为3:5:7,与它相似的三角形的最长边为21cm,则其余两边之和为( )
A.32cm B.24cm C.18cm D.16cm
6. 已知⊿ABC∽⊿A′B′C′，且BC：B′C′= AC：A′C′，若AC=3，A′C′=1.8，则△A′B′C′与△ABC的相似比是（ ）。
A. 2:3 B. 3:2 C. 5:3 D. 3:5
7.可以判定
∽
，的条件是
（ ）
A、∠A=∠
=∠
B、
，且∠A=∠
C、
且∠A=∠ D、以上条件都不对
8. 已知一次函数y=2x+2与x轴y轴交于A、B两点，另一直线y=kx+3交x轴正半轴于E、交y轴于F点，如⊿AOB与E、F、O三点组成的三角形相似，那么k值为（ ）
A 1.5 B 6 C 1.5或6 D 以上都不对
(二)耐心想，填一填（每小题3分,共24分）
9. 已知一个三角形三边长是6cm，7.5cm，9cm，另一个三角形的三边是8cm，10cm，12cm，则这两个三角形 （填相似或不相似）
10. 在1:的中国政区图上，量得福州到北京的距离为6cm，则福州到北京的实际距离为 km。
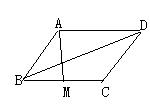
11. 如图，平行四边形ABCD中，M是BC的中点，且AM=9，BD=12，AD=10，则该平行四边形的面积是_____________
12.四边形ABCD∽四边形A,B,C,D, ∠A=70度，∠B,=108度，∠C,=92度 则∠D=_______
13.在平行四边形ABCD中，AB=10，AD=6，E是AD的中点，在AB上取一点F，使⊿CBF∽⊿CDE，则BF的长为________
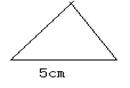
14.如图所示,有一块呈三角形的草坪,其一边长为20m,在这个草坪的图纸上,若这条边的长为5cm, 其他两边的长都是3.5cm, 则该草坪其他两边的实际长度为_________.
15.在直角坐标中,已知点A(-2,0),B(0,4),C(0,3),过点C的直线交x轴于点D,使得以D,O,C为顶点的三角形与∽⊿AOB相似,这样的直线最多可以作____条.
16.已知AB是⊙O的直径，AB=12cm,CD是⊙O一条弦，它与AB交于点E，
⊿ACE与⊿BDE的面积之比为4:1,则AC：BD=_____
(三)动手做，解一解（每小题6分, 共24分）
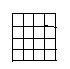
17.在方格纸中，每个小格的顶点叫做格点,以格点连线为边的三角形叫做格点三角形.请你在如图所示的4×4的方格纸中,画出两个相似但不全等的格点三角形(要求:所画三角形为钝角三角形,标明字母,并说明理由).
18.已知⊿△ABC∽⊿DEF且AB=3，AC=4，DE=2，求（1）⊿ABC与⊿DEF的相似比k1 (2) ⊿DEF与⊿ABC的相似比k2 (3) 求EF：BC的值
19.已知⊿ABC、⊿DCE、⊿FEG是三个全等的等腰三角形，底边BC、CE、EG 在同一直线上，且AB=
，BC=1。连接BF，分别交AC、DC、DE于点P、Q、R。
求证：⊿BFG∽⊿FEG，并求BF的长（3）
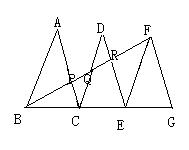
20.如图⊿ABC是等边三角形,点D,E分别在BC,AC上,且BD=CE,AD与BE相交于点F.(1)试说明⊿ABD∽⊿BCE.
(2) ⊿AEF与⊿ABE相似吗?说说你的理由.
四、创新应用（21题8分22题10分，共18分）
21.已知：如图，在正方形ABCD中，P是BC上的点，且BP＝3PC，Q是CD的中点．求证：⊿ADQ∽⊿QCP．
22. ⊿ABC中,AD、CE是中线, ∠BAD=∠BCE,请猜想⊿ABC的形状,并证明.
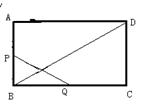
五、探索拓展（共20分）
23.已知矩形ABCD，长BC=12cm，宽AB=8cm，P、Q分别是AB、BC上运动的两点。若P自点A出发，以1cm/s的速度沿AB方向运动，同时，Q自点B出发以2cm/s的速度沿BC方向运动，问经过几秒，以P、B、Q为顶点的三角形与⊿BDC相似？
参考答案
一、选择题
1.B 2.C 3.B 4.C 5.B 6.D 7.D 8.C
二、填空题
9.相似 10.1500 11.72 12.∠D=900 13.1.8 14. 14m 15.4条 16. 2:1
三、解答题
17.略 18 .K1=3:2 K2=2:3 2：3 19.利用BG：FG=EG：FG，∠G=∠G，可证⊿BFG∽⊿FEG，BF=3
20 (1)利用等边三角形的性质可证（2）相似，主要有（1）得∠BAD=∠EBC再证∠FAE=∠ABE
四、21证明（主要步骤）有正方形性质及已知得PC=
BC=CD，DQ=
CD，即：DQ:PC=2:1
QC:AD=2:1 加上直角相等可证相似。 22，等腰三角形。
五题：23，有两种情况：⊿PBQ∽⊿BCD时t1=2 ⊿PBQ∽⊿DCB t2=