***初三第二次月考数学试题卷***
命题人 何德良
考生须知:
1.本试卷分试题卷和答题卷两部分。满分150分,考试时间120分钟。
2.答题时,必须在答题卷密封区内写明班级、姓名和考号。
3.所有答案都必须做在答题卷规定的位置上,务必注意试题序号和答题序号相对应。
4.考试结束后,上交答题卷。
一.选择题(本题有10个小题,每小题4分,共40分)下面每小题给出的四个选项中,只有一个是正确的,请把正确选项前的字母填在答题卷中相应的格子内。
01.已知x=-1是方程x2+mx+1=0的一个实数根,则m的值是
A、0 B、1 C、2 D、-2
02.张华同学的身高为1.6米,某一时刻他在阳光下的影长为2米,同时与他邻近的一棵树的影长为6米,则这棵树的高为
 A、3.2米 B、4.8米 C、5.2米
D、5.6米
A、3.2米 B、4.8米 C、5.2米
D、5.6米
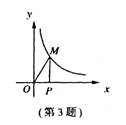
03.反比例函数y=![]() (k>0)在第一象限内的图象如图,点M是图象上一点,MP垂直x轴于点P,如果△MOP的面积为1,那么k的值是
(k>0)在第一象限内的图象如图,点M是图象上一点,MP垂直x轴于点P,如果△MOP的面积为1,那么k的值是
A、 1 B、 2
C、 4 D、![]()
04.下列四个命题中,假命题的是.
A、有三个角是直角的四边形是矩形; B、对角线互相垂直平分且相等的四边形是正方形;
C、四条边都相等的四边形是菱形; D、顺次连接一个四边形各边中点,得到一个菱形,那么这个四边形是等腰梯形.
05.函数y=(2m-1)x是正比例函数,且y随自变量x的增大而增大,则m的取值范围是
A、m>![]() B、m<
B、m<![]() C、m≥
C、m≥![]() D、m≤
D、m≤![]()
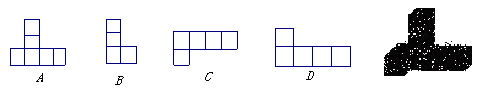 06.右边几何体的俯视图是
06.右边几何体的俯视图是
07.下列关于反比例函数的叙述,不正确的是
A、反比例函数y=![]() 的图象绕原点旋转180°后,能与原来的图象重合;
的图象绕原点旋转180°后,能与原来的图象重合;
B、反比例函数y=![]() 的图象既不与x轴相交,也不与y轴相交;
的图象既不与x轴相交,也不与y轴相交;
C、经过反比例函数y=![]() 的图象上任意一点向x轴,y轴作垂线,垂线段与坐标轴围成的矩形面积总等于
的图象上任意一点向x轴,y轴作垂线,垂线段与坐标轴围成的矩形面积总等于![]() ;
;
D、反比例函数y=![]() ,当k>0时,y随x的增大而减少。
,当k>0时,y随x的增大而减少。
 08.如图, 等腰梯形两底之差等于一腰的长,那么这个梯形
08.如图, 等腰梯形两底之差等于一腰的长,那么这个梯形
较小内角的度数是
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
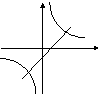
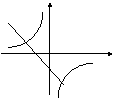 09. 如图,
在同一坐标系中(水平方向是x轴),函数
09. 如图,
在同一坐标系中(水平方向是x轴),函数![]() 和
和![]() 的图象大致是
的图象大致是
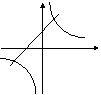 |  |  |
A B C D
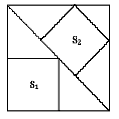 10.如图,大正方形中有2个小正方形,如果它们的面积分别是
10.如图,大正方形中有2个小正方形,如果它们的面积分别是
S1、S2 ,那么S1、S2的大小关系是
A、 S1 > S2 B、 S1 = S2
C、 S1 < S2 D、 S1、S2 的大小关系不确定
二.填空题(本题有6个小题,每小题5分,共30分)
请把正确答案填在答题卷中相应的格子内。
11.一次函数![]() 的图象经过A(-3,0)和B(O,2)两点,则
的图象经过A(-3,0)和B(O,2)两点,则![]() >0的解集是 .
>0的解集是 .
12. 等腰三角形的底和腰的长是方程![]() 的两个根,则这个三角形的周长为 .
的两个根,则这个三角形的周长为 .
13.已知双曲线![]() 经过点(-1,3),如果A(
经过点(-1,3),如果A(![]() ),B(
),B(![]() )两点在该双曲线上,且
)两点在该双曲线上,且![]() <
<![]() <0,那么
<0,那么![]()
![]() .
.
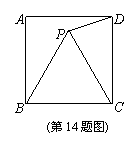
14.如下左图,已知正方形ABCD的边长为m,△BPC是等边三角形,则△CDP的面积为
___ (用含m的代数式表示) .
15.如下右图,某同学从A点出发前进10米,向右转18°,再前进10米,又向右转18°,这样下去,他第一次回到出发点A时,一共走了___________米.
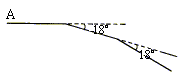
(第15题图)
16.已知:直角三角形的两边长分别是6和8,那么这个直角三角形的另一条边的长是___________。
初三第二次月考数学试题卷答题卷
总分
一. 选择题(本题有10个小题,每小题4分,共40分)
| 题号 | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 10 |
| 答案 |
二. 填空题(本题有6个小题,每小题5分,共30分)
| 题号 | 11 | 12 | 13 | 14 | 15 | 16 |
| 答案 |
三.解答题(本题有8小题,第17~20题每题8分,第21题10分,第22、23题每题12分,第24题14分,共80分)解答应写出文字说明、证明过程或推演步骤。
17. (本小题满分8分)解下列方程:
(1)![]() (2)
(2)![]()
18.(本小题满分8分)已知![]() 是y关于x的反比例函数,且图象在第二、四象限,求m的值.
是y关于x的反比例函数,且图象在第二、四象限,求m的值.
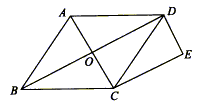
19.(本小题满分8分) 如图,O是菱形ABCD对角线的交点,作DE∥AC,CE∥BD,DE、CE交于点E,四边形OCED是矩形吗?证明你的结论。
20.(本小题满分8分) 已知下列n(n为正整数)个关于x的一元二次方程:
①![]() ②
②![]() ③
③![]()
![]() (n)
(n)![]()
⑴请解上述一元二次方程①、②、③、(n);
⑵请你指出这n 个方程的根具有什么共同特点,写出一条即可。
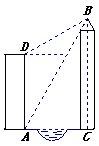 21.(本小题满分10分)如图,小丽的家住在世通华庭的电梯公寓AD内,她家的对面新建了一座大厦BC。为了测得大厦的高度,小丽在她家的楼底A处测得大厦顶部B的仰角为60º,爬上楼顶D处测得大厦的顶部B的仰角为30º。已知小丽所住的电梯公寓高82米,请你帮助小丽计算出大厦高度BC及大厦与小丽所住电梯公寓间的距离AC。
21.(本小题满分10分)如图,小丽的家住在世通华庭的电梯公寓AD内,她家的对面新建了一座大厦BC。为了测得大厦的高度,小丽在她家的楼底A处测得大厦顶部B的仰角为60º,爬上楼顶D处测得大厦的顶部B的仰角为30º。已知小丽所住的电梯公寓高82米,请你帮助小丽计算出大厦高度BC及大厦与小丽所住电梯公寓间的距离AC。
(计算结果保留根号)
22.(本小题满分12分)你还记得图形的旋转吗?如图,P是正方形ABCD内一点,PA=a,PB=2a,PC=3a.将△APB绕点B按顺时针方向旋转,使AB与BC重合,得△CBP,.
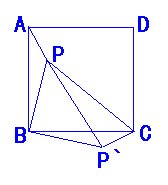 ⑴ 求证:△PBP,是等腰直角三角形;
⑴ 求证:△PBP,是等腰直角三角形;
⑵ 猜想△PCP,的形状,并说明理由.
23.(本小题满分12分)已知反比例函数![]() 和一次函数
和一次函数![]() ,其中一次函数
,其中一次函数
图象经过(a,b)与(a+1,b+k)两点.
(1) 求反比例函数的解析式.
(2) 如图,已知点A是第一象限内上述两个函数图象的交点,求A点坐标.
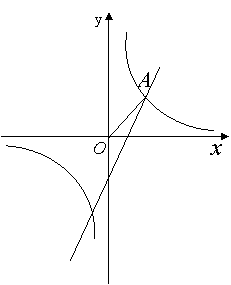 (3) 利用(2)的结果,请问:在X轴上是否存在点P,使△AOP为等腰三角形?若存在,把符合条件的P点坐标都求出来;若不存在,请说明理由.
(3) 利用(2)的结果,请问:在X轴上是否存在点P,使△AOP为等腰三角形?若存在,把符合条件的P点坐标都求出来;若不存在,请说明理由.
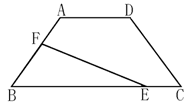
24.(本小题满分14分)如图,在等腰梯形ABCD中,AB=DC=5,AD=4,BC=10. 点E在下底边BC上,点F在腰AB上.
(1)若EF平分等腰梯形ABCD的周长,设BE长为x,试用含x的代数式表示△BEF的面积;
(2)是否存在线段EF将等腰梯形ABCD的周长和面积同时平分?若存在,求出此时BE的长;若不存在,请说明理由;
(3)是否存在线段EF将等腰梯形ABCD的周长和面积同时分成1∶2的两部分?若存在,求出此时BE的长;若不存在,请说明理由.
 |
初三第二次月考数学试题卷参考答案
一. 选择题(本题有10个小题,每小题4分,共40分)
| 题号 | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 10 |
| 答案 | C | B | B | D | A | C | D | B | A | A |
二. 填空题(本题有6个小题,每小题5分,共30分)
| 题号 | 11 | 12 | 13 | 14 | 15 | 16 |
| 答案 | X>-3 | 10 | < |
| 200 | 10或 |
三.解答题(第17~20题每题8分,第21题10分,第22、23题每题12分,第24题14分,共80分)解答应写出文字说明、证明过程或推演步骤。
17.解:(1) ![]() ……4分
(2)
……4分
(2) ![]() ……4分
……4分
18. 解:由题意可得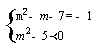 ……3分 解方程得
……3分 解方程得![]()
![]() ……3分
……3分
但![]() 不合题意,舍去。所以
不合题意,舍去。所以![]() 。………2分
。………2分
19. 四边形OCED是矩形。……3分 证明略。……5分
20.解:(1)①![]() 所以
所以![]()
②![]() 所以
所以![]()
③![]() 所以
所以![]() ……
……
(n)![]() 所以
所以![]() …………6分
…………6分
(2)共同特点是:都有一个根为1;都有一个根为负整数;
两个根都是整数根等等 …………………………………2分
21. 解:过D作DE⊥BC垂足为E …………1分

![]()

![]() 设BE=x米,在Rt△BDE中,∠BDE=30°,BE=x
设BE=x米,在Rt△BDE中,∠BDE=30°,BE=x
![]() ∴ DE=
………… 2分
∴ DE=
………… 2分
![]()
![]()
![]()
![]()
![]()
![]()
![]() 在Rt△ABC中,∠BAC=60°,BC=82+x
在Rt△ABC中,∠BAC=60°,BC=82+x
![]() ……………2分
……………2分
∵ DE=AC 即 解得x=41…2分
∴ BC=82+41=123(米) ………………1分
![]() AC= (米) ………………1分
AC= (米) ………………1分
![]()
![]()
![]() 答:大厦高度BC为123米,
答:大厦高度BC为123米,
![]() 大厦和电梯公寓的距离AC= 米 ………1分
大厦和电梯公寓的距离AC= 米 ………1分
22.解:(1)证明:由图形旋转可知: △APB≌△CP′B , ……………2分
∴BP=BP′=2a, AP=CP′=a.且∠ABP=∠CBP′………2分
由四边形ABCD是正方形,得∠ABC=90°,
∴∠PBP′=90, ∴△PBP′是等腰直角三角形。………4分
(2) 由(1)所证△PBP′是等腰直角三角形,
∴PP′= ![]()
![]() ,
……………2分
,
……………2分
在△PP′C中,PP′=![]() ,PC =
,PC = ![]() ,CP′=
,CP′= ![]()
且![]() ……………2分
……………2分
∴△PCP,是直角三角形

 24.解:(1)∵EF平分等腰梯形ABCD的周长,
24.解:(1)∵EF平分等腰梯形ABCD的周长,
∴BF=12-x, FG = ![]()
∴![]() ………5分
………5分
(2)∵![]()
∴当![]() ,
,![]() = 14 解得
= 14 解得![]()
![]()
∵当![]() 时,BF=12-x =7>AB,不合题意。
时,BF=12-x =7>AB,不合题意。
∴当BE=7时,线段EF将等腰梯形ABCD的周长和面积同时平分。………5分(3)当线段EF将等腰梯形ABCD的周长和面积同时分成1∶2的两部分时,
①若BE+BF=8,则FG = ![]() , 有
, 有 ![]()
这个方程无实数解;
②若BE+BF=16,而BC+AB=15,这种情况是不可能的;
∴不存在线段EF将等腰梯形ABCD的周长和面积同时分成1∶2的两部分。………………………………………………………………4分