九年级数学阶段性测试
命题人：陈世文
考生须知：
1．全卷满分为150分，考试时间120分钟．试卷2张共4页，有三大题，24小题．
2．本卷答案必须做在答题卷的相应位置上，做在试卷上无效．
3．请用钢笔或圆珠笔将姓名、准考证号分别填写在答题卷的相应位置上．
温馨提示：请仔细审题，细心答题，相信你一定会有出色的表现
试 卷 Ⅰ
一. 选择题（本题共10小题，每小题4分，共40分，请选出各题中一个符合题意的正确选项，不选、多选、错选均不给分）
1． 方程
的根是（ ▲
）
（A）
（B）
（C）
（D）
2．下列图形中，是中心对称图形，但不是轴对称图形的是（ ▲ ）
（A）正方形 （B）矩形 （C）菱形 （D）平行四边形
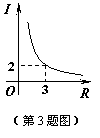
3．某闭合电路中，电源电压为定值，电流I（A）与电阻R（Ω）成反比例，如图表示的是该电路中电流I与电阻R之间函数关系的图象，则用电阻R表示电流I的函数解析式为（ ▲ ）
（A）
（B）
（C）
（D）
4．把方程
配方得（ ▲ ）
（A）
（B）
（C）
（D）
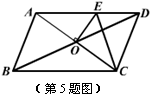5. 如图，□ABCD的周长为
，AC、BD相交于点O，OE⊥AC交AD于E，则△DCE的周长为（ ▲ ）
（A）4 
（B）6
（C）8 （D）10
6．根据下列表格的对应值：
|
| 3.23 | 3.24 | 3.25 | 3.26 |
|
| -0.06 | -0.02 | 0.03 | 0.09 |
判断方程
的一个解
的范围是（ ▲ ）
（A）
（B）
（C）
（D）
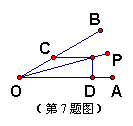
7．如右图∠AOP=∠BOP=15º，PC∥OA，PD⊥OA，若PC=4，
则PD等于（ ▲ ）
（A）4 （B）3 （C）2 （D）1
8．下列函数中，当
时，
随的增大而减小的是（ ▲ ）
（A）
（B）
（C）
（D）
9．如图，正比例函数
与反比例函数
的图
象相交于A，C两点，过点A作轴的垂线交轴于点B，连接B，
C，若△ABC的面积记为S，则（ ▲ ）
（A）S=1 （B）S=2
|
值有关
10．△ABC的周长为16，连接△ABC三边的中点构成第一个三角形，再连接这个新三角形的各边中点构成第二个三角形，依次类推，则第2006个三角形的周长为（ ▲ ）
（A）
（B）
（C）
（D）
 |
试 卷 Ⅱ
二、填空题（本题有6小题，每小题5分，共30分）
11．已知一元二次方程有一根为1，那么这个方程可以是 ▲ 。(只需写出一个方程)
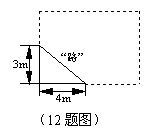
12．如图，学校有一块长方形花坛，有极少数人为了避开拐角走“捷径”，在花坛内走出了一条“路”. 他们仅
仅少走了 ▲ m，却踩伤了花草。
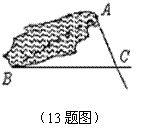
13．如图，为了求出湖两岸A、B两点之间的距离，小明从A、B两点分别测得∠BAC＝90°，∠ABC＝30°，又量得BC＝160 m，则A、B两点之间的距离为 ▲ m。（结果保留根号）。
|
14．已知点
都在反比例函数
上，则
的大小关系是 ▲
。
15．三角形的两边长分别为3和6，第三边的长是方程
的一个根，则这个三角形的周长是 ▲ 。
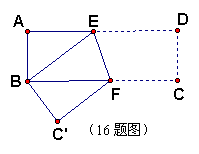
16．如图，矩形纸片ABCD的长AD=9cm，宽AB=3cm，将这张纸片折叠，使点D与点B重合，那么折叠后DE
的长为 ▲ cm，折痕EF的长为 ▲ cm。
三、解答题（本题有8小题，第17题6分，18～20题每题8分，21～23题每题12分，第24题14分，共80分）
友情提示：做解答题，别忘了写出必要的过程噢！
17．解方程：
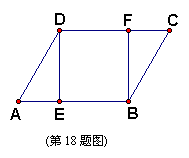
18．如图，在□ABCD中，E，F分别是AB，CD上的点，
且AE=CF，求证：DE=BF。
19．我市统计局关于经济和社会发展统计指出，2001~2004全社会用电量的折线统计图如图
（1）填表：2001~2004全市社会用电量统计表
| 年 份 | 2001 | 2002 | 2003 | 2004 |
| 社会用电量（单位：亿千瓦时） |
（2）根据我市2002年至2004年用电量统计数据，求这两年年平均增长的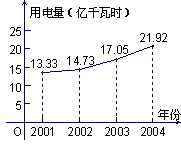
百分率（保留两个有效数字）
20．我们在探索平面图形的性质时，往往通过剪拼的方式帮助我们寻找解题思路．
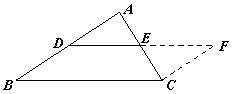例如，在证明三角形中位线定理时，就采用了如图的剪拼方式，将三角形转化为平行四边形使问题得以解决．
（1）请你将图1的平行四边形剪拼为矩形；
（2）请你将图2的梯形剪拼为三角形．
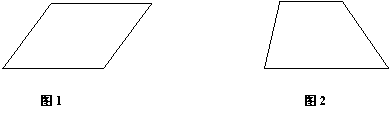要求：作出裁剪线，保留痕迹，不写作法，画图工具不限．
21．某商场将进货价为30元的台灯以40元售出，平均每月能售出600个。调查表明：这种台灯的售价每上涨1元，其销售量就将减少10个，为了实现平均每月10000元的销售利润，这种台灯的售价应定为多少？这时应进台灯多少个？
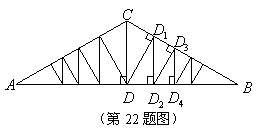22．如图，等腰
中，
，
是底边上的高，
．
（1）与
有什么数量关系？请说明理由；
（2）过点
作
，垂足为
；
，
垂足为
；
，垂足为
；
，垂足为
；…；
，垂足为
；
，垂足为
（
为非零自然数）．若
，请用含
的代数式表示下表中线段的长度（请将结果直接填入表中）；
| 线段 |
|
|
| … |
|
| 长度 |
| … |
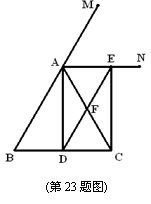
23．(本题12分)已知：如图，在△ABC中，AB＝AC，AD
BC，垂足为D，AN是△ABC外角
CAM的平分线，CEAN，垂足为E，连接DE交AC于F
（1）求证：四边形ADCE为 矩形 （2）求证：DF∥AB，DF＝
AB
（3）当△ABC满足什么条件时，四边形ADCE是一个正方形？简述你的理由。
 |  | ||
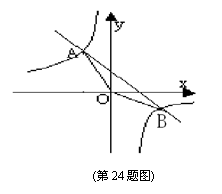24．本题14分).已知一次函数
的图象与反比例函数
的图象相交于A、B两点，坐标分别为(—2，4)、（4，—2）。
（1）求两个函数的解析式；
（2）结合图象写出
时，x的取值范围；
（3）求△AOB的面积；
（4）是否存在一点P，使以点A﹑B﹑O﹑P为顶点的四边形为菱形？若存在，求出顶点P的坐标；若不存在，请说明理由。