九年级数学期中考试试卷
考生注意：本试卷共四页，满分120分
|
题 号 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 总分 |
|
得 分 |
|
|
|
|
|
|
|
一. 填空：（每题2分，共30分）
1.
实数
在数轴上的位置如图所示，则
；
|
0 1 2 3
2. 已知
是整数，则正整数
的最小值是
；
3. 已知
，
，
，则代数式
；
4. 用长3㎝，宽2.5㎝的邮票300枚摆成一个正方形，则这个正方形的边长是 ㎝；
5. 有一人掌握了某项新技术，经过两轮帮教后共有121人掌握了此项新技术，每轮帮教中平均一个人帮教
个人；
6. 已知点
与
关于原点
对称，则 
；
|
|
7. 图（2）是将图（1）中△DCE经过一次 得到的；（旋转、平移、轴对称）
|
EE
（1）
（2）
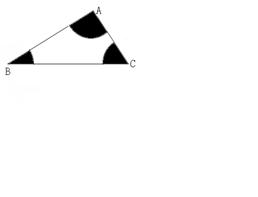
8. 如图，要在面积为400
的三角形广场
的三个角处各修建一个半径相同的扇形草坪，
要求草坪的总面积为广场面积的一半，那么
扇形的半径是
；
9. 如图
，
，则
；
10. 圆锥的底面积直径是80㎝，母线长是90㎝，则它的侧面展开图的圆心角是 度；
11. 如图，
的半径为1，圆心
在正三角形的边
上沿图示方向移动，当移到与
边相切时，
的长为
；
12. 一张圆桌旁有四个座位，
先坐在如图所示的座位上，
、
、
三人随坐在其他三
个座位上，则与相邻而坐的概率是
； A
Ａ Ａ
Ｂ
Ｃ
O
o
D
Ｂ Ｃ
（第9题） （第11题） （第12题）
13. 甲、乙按如下规则做游戏，桌子有5个乒乓球，每次可取1个或2个，由甲先取，最后取完球的获胜。如果甲获胜的概率为1，那么甲第一次应取 个球；
14. 如果一个正
边形的一个外角等于一个内角的
，则 
；
15. 观察规律：
，
，
，…
则
。
二. 选择：（每题3分，共18分）
1.
如图的汽车标志中，是中心对称图形的有（ ）
(A) 1个 (B) 2个 (C) 3个 (D) 4个
2. 下列事件：（1）通常加热到100℃时水沸腾；（2）掷一次骰子点数为6；（3）三角形内角和是180°；（4）经过某一路口正好遇上红灯；（5）一个一元二次方程必有两个实数解，其必然事件有（ ）
（A）5个 （B）4个 （C）3个 （D）2个
3.
某工厂今年产值为
，计划今后平均增长
，那么两年后的产值是（ ）
（A）
（B）
（C）
（C）
4.
若一个三角形的三边长均满足方程
，则此三角形的周长为（ ）
（A）6 （B）10 （C）12 （D）以上都有可能
5. 如图，当两个半径为30㎝的转动轮转动120°角时，
传送带上的物体A平移的距离为（ ） Ａ
（A）10㎝ （B）20㎝
（C）25㎝ （D）30㎝
6.
已知
、
外切，两圆的半径分别为1㎝和3㎝ ，那么半径为5㎝且与、都相切的圆一共可以作（ ）
（A）4个 （B）5个 （C）6个 （D）7个
三. 解下列各题：（每题7分，共21分）
1. 当
时，求代数式
的值；
2. 关于的一元二次方程
有一根为0，求
的值；
3. 袋中装有黄、白各一个小球，除颜色外，其余都相同，随机摸出1个小球后放回，再随机摸出一个，用树形图或列表分析下列事件的概率
（1）第一次摸到黄球，第二次摸到白球；
（2）两次摸到相同颜色的小球。
四. （每题7分，共21分）
1. 如图
和
都是等边三角形，且
三点在一直线上，
可以看作是
经过怎样的图形变换得到的？请说明理由；
Ａ
Ｅ
Ｂ Ｃ Ｄ
2. 如图，的直径为10㎝，弦
为6㎝，
的平分线交于，求四边形
的面积；
D
|
|
|
●
B
3. 如图，内切于点
，且
，设的周长
为，面积为
，的半径为
，
（1）求证：
（2）当
时，求内切圆的半径r。
Ｆ Ｅ
|
Ｂ Ｄ Ｃ
五. 一个小球以5m/s的速度开始向前滚动，并且均匀减速，滚动10m后小球停下来。（1）小球滚动了多少时间?（2）平均每秒小球的运动速度减少多少？（3）小球滚动到5m时约用了多少时间（精确到0.1s）?（10分）
六.
如图，点
在坐标系中的坐标分别为
，求绕轴旋转一周所围成的几何体的表面积。(10分)
y
Ｃ
Ｏ Ａ Ｂ
x
七. （10分）某电脑公司现有A、B、C三种型号的甲品牌电脑，有D、E两种型号的乙品牌电脑，价格如下：A型6000元；B型4000元；C型2500元；D型5000元；E型2000元。某希望中学要从甲乙两种品牌的电脑中各选购一种型号的电脑。
（１） 写出所有的选购方案（利用树形图或列表法表示）
（２） 如果（１）中各选购方案被选中的可能性相同，那么A型号电脑被选中的概率是多少？