九年级数学上第三单元检测试卷 姓名
一.选择题(每小题2分,共12分)
1.一个等腰梯形的两底之差为![]() ,高为
,高为![]() ,则等腰梯形的两底的一个锐角为
( )
,则等腰梯形的两底的一个锐角为
( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
2.在Rt⊿ABC中,∠ACB =![]() ,∠A =
,∠A =![]() ,AC =
,AC =![]() ,则AB边上的中线为 ( )
,则AB边上的中线为 ( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
3.等边三角形一边上高线长为![]() ,那么这个等边三角形的中位线长为 ( )
,那么这个等边三角形的中位线长为 ( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
4.下列判定正确的是 ( )
A 对角线互相垂直的四边形是菱形 B 两角相等的四边形是梯形
C 四边相等且有一个角是直角的四边形是正方形
D 两条对角线相等且互相垂直的四边形是正方形
5.顺次连结等腰梯形各边中点得到的四边形是 ( )
A 矩形 B 菱形 C 正方形 D 平行四边形
6.直角梯形的两个直角顶点到对腰中点的距离 ( )
A 相等 B 不相等 C 可能相等也可能不相等 D 互相垂直
二.填空题:(每小题3分,共24分)
7.已知菱形的周长为![]() ,一条对角线长为
,一条对角线长为![]() ,则这个菱形的面积为
;
,则这个菱形的面积为
;
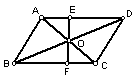 8.如图:EF过平行四边形ABCD的对角线交点O,交AD于E,交
8.如图:EF过平行四边形ABCD的对角线交点O,交AD于E,交
BC于F,已知AB =![]() ,BC =
,BC =![]() ,OE =
,OE =![]() ,那么四边形EFCD的周长
,那么四边形EFCD的周长
为 ;
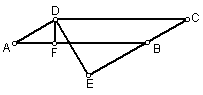 9.已知,如图:平行四边形ABCD中,AB =
9.已知,如图:平行四边形ABCD中,AB =![]() ,AB边上
,AB边上
的高为![]() ,BC边上的高为
,BC边上的高为![]() ,则平行四边形ABCD的
,则平行四边形ABCD的
周长为 ;
10.⊿ABC中,AB = AC =![]() ,∠BAC的平分线AD交
,∠BAC的平分线AD交
BC于D,则D点到AB的距离为 ;
 11.如图,在Rt⊿ABC中,∠C =
11.如图,在Rt⊿ABC中,∠C =![]() ,AC = BC,AB =
,AC = BC,AB =![]() ,
,
矩形DEFG的一边在AB上,顶点G、F分别在AC、BC上,
D、E在AB上,若DG:GF =1:4,则矩形DEFG的面积
为 ;
12.在⊿ABC和⊿ADC中:下列论断:①AB = AD;
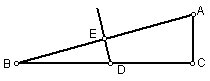 ②∠BAC =∠DAC;③BC = DC,把其中两个论断作为条件,另一个论断作为结论,写出一个真命题是:
;
②∠BAC =∠DAC;③BC = DC,把其中两个论断作为条件,另一个论断作为结论,写出一个真命题是:
;
13.如图,在⊿ABC中,∠C =![]() ,∠B =
,∠B =![]() ,AB的
,AB的
垂直平分线交AB于D,交BC于D,DB =![]() ,
,
那么AC = ;
14.在⊿ABC中,∠C =![]() ,周长为
,周长为![]() ,斜边上的中线CD =
,斜边上的中线CD =![]() ,则Rt⊿ABC的面积为
;
,则Rt⊿ABC的面积为
;
三.(6分)
15.作图题:已知三个村庄的位置如图,三村联合打一口井,向三个村庄供水,使水井到三个村庄的距离相等,水井的位置设在何处?请用尺规画出水井位置,不写作法,保留痕迹。
![]()
![]()
![]()
四.解答证明题:
16.(8分)在平行四边形ABCD中,BC = 2AB,E为BC中点,求∠AED的度数;
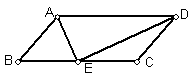
17.(10分)如图,四边形ABCD中,AD = BC,AE⊥BD,CF⊥BD,垂足为E、F,BE = DF,求证:四边形ABCD是平行四边形;

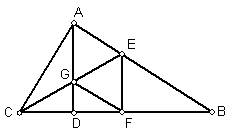 18.如图:在⊿ABC中,∠BAC =
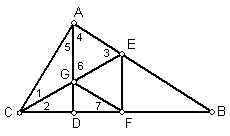
18.如图:在⊿ABC中,∠BAC =![]() ,AD⊥BC于D,CE平分∠ACB,交AD于G,交AB于E,EF⊥BC于F,求证:四边形AEFG是菱形;
,AD⊥BC于D,CE平分∠ACB,交AD于G,交AB于E,EF⊥BC于F,求证:四边形AEFG是菱形;
19.(10分)如图,以正方形ABCD的对角线AC为一边,延长AB到E,使AE = AC,以AE为一边作菱形AEFC,若菱形的面积为![]() ,求正方形边长;
,求正方形边长;

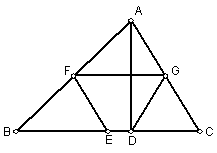
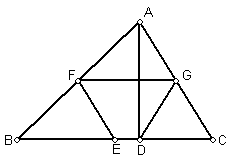
20.(10分)如图AD是⊿ABC边BC边上的高线,E、F、G分别是AB、BC、AC的中点,求证:四边形EDGF是等腰梯形;
21.如图,AC、BD是矩形ABCD的对角线,AH⊥BD于H,CG⊥BD于G,AE为∠BAD的平分线,交GC的延长线于E,求证:BD = CE;

参考答案:
一选择题(每小题2分,共12分)
1.B;2.A;3.C;4.C;5.B;6.A;
二.填空题:(每小题3分,共24分)
7.![]() ;
;
8.![]() ;
;
9.![]() ;
;
10.![]() ;
;
11.![]() ;
;
12.①,③![]() ②或①,②
②或①,②![]() ③;
③;
 13.
13.![]() ;
;
14.![]() ;
;
三.15.有铅笔作图痕迹,有点O为所作点为水井的结论。
四.16.
证1:∵ E为BC中点,
∴BE = EC =![]() BC,
BC,
∵BC = 2AB
∴AB = BE = EC = DC
∴∠BAE =∠BEA,∠CED =∠CDE
∵四边形ABCD是平行四边形
∴∠B +∠C =![]()
∴∠BAE +∠BEA+∠CED +∠CDE +∠B +∠C =![]()
∴2(∠BEA +∠CED)+![]() =
=![]()
∴∠BEA +∠CED =![]()
∴∠AED =![]() (∠BEA +∠CED)=
(∠BEA +∠CED)=![]()
 其他证法正确的也给分。
其他证法正确的也给分。
17.证:∵BE = DF,EF = EF,
∴BE + EF = DF + EF
∴BF = ED
∵AD = BC,AE⊥BD,CF⊥BD,
∴⊿AED≌⊿CFB
∴AD = BC
∴∠ADB =∠CBD
∴AD∥BC
 ∴四边形ABCD是平行四边形
∴四边形ABCD是平行四边形
18.证:
∵CE平分∠ACB,EA⊥CA,EF⊥BC
∴AE = FE
∵∠1 =∠2
∴⊿AEC≌⊿FEC
∴AC = FC
∵CG = CG
∴⊿ACG≌⊿FCG
∴∠5 =∠7 =∠B
∴GF∥AE
∵AD⊥BC,EF⊥BC
∴AG∥EF
∴
∵AG =GF(或AE = EF)
∴四边形AGFE是菱形(一组邻边相等的平行四边形是菱形)
 用其他方法证明也可。
用其他方法证明也可。
19.解:设正方形的边长为![]()
∵AC为正方形ABCD的对角线
∴AC =![]()
∴![]()
∴![]()
∴![]()
 舍去
舍去![]()
答:正方形的边长为![]() 。
。
20.证:∵F、G、E分别为AB、AC、BC的中点,
∴FG ∥BC,FE ∥GC
∴EF = GC =![]() AC
AC
∵在Rt⊿ADC中,
∵DG为斜边AC边上的中线
∴DG =![]() AC
AC
∴EF = DG
∵FG ∥BC
∴FG ∥DE且FG![]() DE
DE
∴四边形EDGF是等腰梯形。(其他证法合理也给分)
 |
21.证:∵矩形ABCD的对角线AC、BD
∴AC = BD
且有:AB = DC,∠BAD =∠CDA =![]()
AD = AD
∴⊿BAD≌⊿CDA
∴∠1 =∠4
∵AH⊥BD
∴∠2 +∠3 =![]() ,而∠1 +∠2 =
,而∠1 +∠2 =![]()
∴∠3 =∠1 =∠4
∵AE平分∠BAD
∴∠3 +∠5 =∠6 +∠4
∴∠5 =∠6
∵AH⊥BD,EG⊥BD
∴AH∥GE
∴∠5 =∠E
∴∠E =∠6
∴AC = CE = BD
∴BD = CE