中考数学模拟试卷
（华东师大版）
时间：120分钟 满分：150
一、选择题:（本题共10小题，每小题4分，共40分. 在每题所给出的四个选项中，只有一项是符合题意的. 请把所选项前的字母代号填在题后的括号内.）
1．函数
中自变量x的取值范围是 （ ）
A．x≠－1 B．x>－1 C．x≠1 D．x≠0
2．已知x=－1是方程x2+mx+1=0的一个实数根，则m的值是（ ）
A、0 B、1 C、2 D、－2
3．四张完全相同的卡片上，分别画有圆、矩形、等边三角形、等腰梯形，现从中随
机抽取一张，卡片上画的恰好是中心对称图形的机会是（ ）
A．
B．
C．
D．1
4．如图所示，在边长为a的正方形中挖去一个边长为b的小正方形（a>b），再把剩余的部分剪拼成一个矩形，通过计算图形（阴影部分）的面积，验证了一个等式是（ ）
A、
B、
C、
D、
5．在“抛一枚均匀硬币”的实验中，如果现在没有硬币，则下面各个试验中哪个不能代替（ ）
A、两张扑克，“黑桃” 代替“正面”，“红桃” 代替“反面”;
B、两个形状大小完全相同，但一红一白的两个乒乓球;
C、扔一枚图钉;
D、人数均等的男生、女生，以抽签的方式随机抽取一人.
6．相信同学们都玩过万花筒，右图是某个万花筒的造型， 图中的小三角形均是全等的等边三角形，那么图中的菱形AEFG可以看成是把菱形ABCD以A为旋转中心（ ）
A、顺时针旋转60°得到 B、顺时针旋转120°得到
C、逆时针旋转60°得到 D、逆时针旋转120°得到
7．将一张正方形的纸片按下图所示的方式三次折叠，折叠后再按图所示沿MN裁剪，则可得（ ）
A、多个等腰直角三角形; B、一个等腰直角三角形和一个正方形
C、四个相同的正方形; D、两个相同的正方形
8．二次函数
图象的大致位置如图，下列判断错误的是（ ）
（A）
（B）
（C）
（D）
9．在匀速运动中，路程s(千米)一定时，速度v(千米/时)关于时间t(小时)的函数关系的大致图象是（ ）
 |
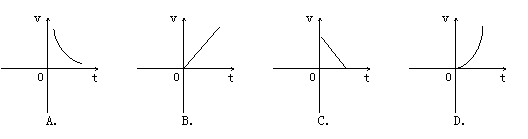10．下表是两个商场1至6月份销售某种商品的情况(单位：箱)
| 1月 | 2月 | 3月 | 4月 | 5月 | 6月 | |
| 甲商场 | 450 | 440 | 480 | 420 | 576 | 550 |
| 乙商场 | 480 | 440 | 470 | 490 | 520 | 516 |
根据以上信息可知
A．甲比乙的月平均销售量大 B．甲比乙的月平均销售量小
C．甲比乙的销售稳定 D．乙比甲的销售稳定
二、填空题:（本大题共有5小题，每题4分，共20分．请把结果直接填在题中的横线上．）
11．在实数内分解因式：x4－2x2= .
12．一个矩形的周长为60㎝，其面积为S，则S的取值不超过 ㎝2.
13．在下面等式的
内填数， 内填运算符号，使等号成立(两个算式中的运算符号不能相同)：
14. 某住宅小区6月份随机抽查了该小区6天的用水量(单位：吨)，结果分别是30、34、32、37、28、31，那么，请你估计该小区6月份(30天)的总用水量约是 吨.
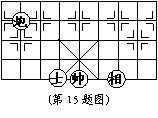
15．如图，如果 所在位置的坐标为(-1,-2), 所
在位置的坐标为(2,-2), 那么， 所在位置的坐
标为 .
三、（本大题共2小题，每题8分，共16分. ）
16．已知不等式5（x-2）+8<6（x-1）+7的最小整数解是方程2x-ax=4的解，求a的值.
17．先化简，再求值：
， 其中
四、（本大题共2小题，每题8分，共16分. ）
18．
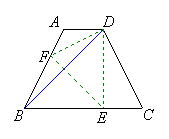如图，等腰梯形ABCD中，AD∥BC，∠DBC=45°．翻折梯形ABCD，使点B重合于点D，折痕分别交边AB、BC于点F、E，若AD=2，BC=8，
求：（1）BE的长；（2）∠CDE的正切值．
19． 如图，给出五个条件：①AE平分∠BAD，②BE平分∠ABC，③E是CD的中点，④AE⊥EB，⑤AB=AD+BC.
（1）请你以其中三个作为命题的条件，写出一个能推出AD∥BC的正确命题，并加以说明；
（2）请你以其中三个作为命题的条件，写出一个不一定能推出AD∥BC的正确命题，并举例说明.
五、（本大题共2小题，每题10分，共20分. ）
20．夏雪同学调查了班级同学身上有多少零用钱，将每位同学的零用钱记录下来，下面是全班40名同学的零用钱的数目（单位：元）
2，5，0，5，2，5，6，5，0，5，5，52，5，8，0，5，5，2，5，
5，8，6，5，2，5，5，2，5，6，5，5，0，6，5，6，5，2，5，0.
（1）请你写出同学的零用钱（0元，2元，5元，6元8元）出现的频数；
（2）求出同学的零用钱的平均数、中位数和众数；
（3）假如老师随机问一个同学的零用钱，老师最有可能得到的回答是多少元？
21.图1是某市年生产总值统计图，根据此图完成下列各题：
(1)2003年某市的生产总值达到 亿元，约是1997年的 倍(倍数由四舍五入法精确到个位)；
(2)小王把图1的折线统计图改为条形统计图，但尚未完成(如图2)，请你帮他完成该条形图；
(3)2003年某市年生产总值与2002年相比，增长率是 %(结果保留三个有效数字)；
(4)已知2003年某市的总人口是139.19万，那么该年某市人均生产总值约是
元(结果保留整数).
六、（本大题共2小题，每题12分，共24分. ）
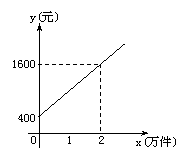
22．某公司市场营销部的营销员的个人月收入与该营销员每月的销量成一次函数关系，其图象如图所示. 根据图象提供的信息，解答下列问题：
(1)求出营销人员的个人月收入y元与该营销员每月的销售量x万件(x≥0)之间的函数关系式；
(2)已知该公司营销员李平5月份的销售量为1.2万件，求李平5月份的收入.
 |
23. 如图，在△ABC中，∠C=90°，AC=6，BC=8，M是BC的中点，P为AB上的一个动点，（可以与A、B重合），并作∠MPD=90°，PD交BC（或BC的延长线）于点D.
（1）记BP的长为x，△BPM的面积为y，求y关于x的函数关系式，并写出自变量x的取值范围；
（2）是否存在这样的点P，使得△MPD与△ABC相似？若存在，请求出x的值；若不存在，请说明理由.
七、（本题满分14分）
24． 
如图，已知AB是⊙O的直径，AC是⊙O的弦，点D是弧ABC中点，弦DE⊥AB，垂足为F，DE交AC于点G.
（1）图中有哪些相等的线段？（要求：不再标注其他字母，找结论的过程中所作的辅助线不能出现在结论中，不写出推理过程）
（2）若过点E作⊙O的切线ME，交AC的延长线于点M（请补完整图形），试问：ME=MG是否成立？若成立，请证明；若不成立，请说明理由.
（3）在满足第（2）问的条件下，已知AF=3，FB=
，求AG与GM的比.〖第（1）的结论可直接利用〗
参考答案：
一、选择题
1．A．分母x+1≠0。
2．C．x=-1代入方程中即得。
3．B．由于圆、矩形是中心对称图形，所以从中随机抽取一张，卡片上画的恰好是中心对称图形的机会。
4．A．在边长为a的正方形中挖去一个边长为b的小正方形，剩余的部分的面积为
，而剩余的部分剪拼成一个矩形的面积为
，故选A。
5．C．因为图钉不是一个质地均匀的物体。
6．D．AE是由AB逆时针旋转120°得到。
7．C.解答本题最好用一章正方形的纸按要求去试一试。
8．B．开口向下说明；与
轴的交点在
轴的上方，说明；对称轴在轴的右边，说明
．
9．A．因为
，所以速度v(千米/时)关于时间t(小时)的函数关系是反比例函数。
10．D．甲和乙的月平均销售量相同，但甲的月销售量的最大量比乙大和最小量比乙小。
二、填空题
11．
12．225．设一边长为x，则另一边长为30-x，从而S=x（30-x）=-x2+30x=-（x-15）2+225
13．如-1-5=-6，3×（-2）=-6等。
14．960．6天的平均用水量是32，该小区6月份(30天)的总用水量约是32×30=960。
15．（-3，1）。通过士与象所在的位置，确定坐标系可得炮所在的位置是（-3，1）。
16．解。由5（x-2）+8<6（x-1）+7得：
x＞-3…………………………………………………………………………4分
所以x=-2。………………………………………………………………………………6分
将x=-2代入2x-ax=4中解得a=4。……………………………………………………8分
17．解。
………………………………5分
当代入有：=
…………8分
18．解：（1）∵∠DBC=45°
∴∠EDB=45°，
∴DE⊥BC，………………………………………………3分
∵ABCD是等腰梯形，
∴EC=3，BE=5；………………………………5分
（2）∵DE=BE=5，CE=3，
∴∠CDE=
．………………………………8分
19．解：（1） ①②⑤
AD∥BC . ………………………………2分
证明：在AB上取点M，使AM＝AD，连结EM，可证△AEM≌△AED, △BEM≌△BCE，∴∠D=∠AME, ∠C=∠BME，故∠D+∠C＝∠AME+∠BME＝180°
∴AD∥BC. ………………………………5分
（2）①②③ AD∥BC为假命题 反例 ：
△ABM中，E是内心，过E作DC⊥EM，显然有，AE平分∠BAM，BE平分∠ABM，ED=EC,但AD不平分于BC. ………………………………8分
20．解： （1）0元的频数是5，2元的频数是7，5元的频数是21，6元的频数是5，8元的频数是2. ………………………………………………………………4分
（2）平均数是4.125，中位数是5，众数是5. ……………………8分
（3）5元. ……………………………………………………………10分
21．解.(1)238.18, 19 (2)作图(略) (3) 13.0, (4) 17112元
说明：每答对1空得2分.作图正确2分。
22．解．(1)依已知条件可设所求的函数关系式为y=kx+b …………………………… 1分
∵函数图象过(0,400)和(2,1600)两点
∴
…………………………………… 4分
解这个方程组，得
…………………………………… 7分
∴所求的函数关系式为y=600x+400 ……………………………… 9分
(2)当x=1.2时，y=600×1.2+400=1120(元) …………………………… 11分
即李平5月份的收入为1120元. ……………………………… 12分
23．解．（1）作PK⊥BC于K，BM＝4，AB＝10，
∵PK∥AC，∴
=
pk＝
x，
∴y＝
×4×x＝
x（0<x<10）.………………………………………………5分
（2）①∠PMB=∠B,
PM=PB ,MK=KB=2 , =
， x=2.5；………………………7分
②∠PMD=∠A,
又∠B =∠B，∴△BPM∽△BAC，
∴BP·AB＝BM·BC，
∴10x=4×8 ，x＝3.2，……………………………………………………11分
∴存在 x＝2.5或3.2. ……………………………………………………12分
24．解. （1）OA=OB，DF=EF，DE=AC，AG=DG，EG=CG. ………………………………3分
（2）ME=GM. 理由是：连EO并延长交⊙O于点N，连结DN.
∵EM是⊙O的切线，
∴∠OEM=90º，∴∠GEM+∠GEN=90º. …………………………………………5分
∵EN是⊙O的直径，∠N+∠GEN=90º，
∴∠N=∠GEM. ………………………………………………………………7分
∵AB是⊙O的直径，∴∠B+∠BAC=90º，
∵∠AGF+∠GAF=90º，∴∠AGF=∠B，……………………………………9分
∵∠AGF=∠CGE，∴∠CGE=∠B.
∵AC=DE，∴∠N=∠B，
∴∠GEM=∠CGE，∴MG=ME. ………………………………………………11分
（3）答案：
.…………………………………………………………………14分