初三第一学期第三次联考数学试卷
命题人：和中 殷昌民 审核人：胡明社
本试卷共120分 时间120分钟
| 小计 | 总分 | ||||||||
| 题号 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | |
| 得分 | |||||||||
一、选择题（每小题2分共24分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
（下列各题有四个选项，其中只有一个是正确的，请你选择正确的选项填入上表中）
1、一元二次方程x2-2x-3=0的根为（ ）
A．x1=1，x2=3 B．x1= -1，x2=3
C．x1= -1，x2= -3 D．x1=1，x2= -3
2、下列图形中对称轴最多的是（ ）
A．菱形 B．正方形 C．等腰三角形 D．线段
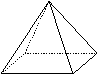
3、如图所示的正四棱锥的俯视图是（ ）
A．
B．
C．
D．
|
A． 
B． 
|
|
D． 
5、一个暗箱里装有10个黑球，8个白球，12个红球，每个球除颜色外都相同，从中任意摸出一个球，摸到白球的概率是（ ）
A．
B．
C．
D．
6、若四边形的两条对角线相等，则顺次连结各边中点所得的四边形是（ ）
A．梯形 B．菱形 C．矩形 D．正方形
|
7、如图，一电线杆AB的高为10米，当太阳光线与地面的夹角为60º时，其影长AC约为( )（
取1.732，结果保留三个有效数字）
A．5.00m B．8.66m
|
|
8、如图，晚上小亮在路灯下散步，在小亮由A处走到B处这一过程中，他在地上的影子（ ）
A．逐渐变短
B．逐渐变长
C．先变短后变长 D．先变长后变短
|
|
9、如图，等腰三角形ABC中，AB=AC，∠A=44º，CD⊥AB于D，则∠DCB等于（ ）
A．44º
B．68º
C．46º
D．22º
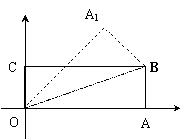
10、如图，在直角坐标系中，将矩形OABC沿OB对折使点A落在A1处，已知OA= 
，AB=1，则点A1的坐标是（ ）
A．（ 
，
）
B．（ ，
3 ）
C．（ ， ）
D．（ 
， ）
11、一个正整数数表如下（表中下一行中数的个数是上一行中数的个数的2倍）
| 第一行 | 1 |
| 第二行 | 2、3 |
| 第三行 | 4、5、6、7 |
| …… | …… |
则第6行的最后一个数为（ ）
A．31 B．63 C．127 D．255
12、水滴滴进下图的玻璃容器中，滴水速度不变，则容器中水的高度随滴水时间变化的图象是（ ）
(A)
(B)
(C) (D)
| 得分 | 评卷人 |
二、填空题（每小题2分共8分）
13、若方程x2-m=0有整数根，则m的值可以是 （填一个可能的值）
14、任意写一个经过二、四象限的反比例函数的关系式：
15、汽车刹车距离S（m）与速度V（km/h）之间的关系式S=
v2,在一辆车速为100km/h的汽车前方80m处，发现一辆故障车，此时刹车 有危险（填：会、不会）
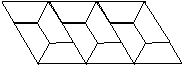16、右图，用12个全等的等腰梯形
镶嵌（密铺）成的图形，这个图形中等腰梯形
的上底长与下底长的比是
| 得分 | 评卷人 |
三、（每小题6分共24分）
17、计算： 2cos60º+2sin30º+4tan45º 18、解方程：2x2+4x-3=0
19、已知：∠AOB，点M、N
求作：点P，使点P到∠AOB两边的距离相等且PM=PN。
（要求：用尺规作图，保留作图痕迹，不写作法）
|
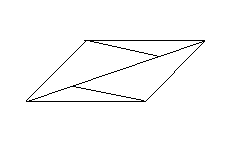求证：（1）△AFD≌△CEB
|
|
| ||||||
|
| |||||
| 得分 | 评卷人 |
四、(第小题7分共14分)
21、如图，天空中有一个静止的广告汽球C，从地面A点测得C点的仰角为45º，从地面B点测得C点仰角为60º，已知AB=20m，点C和直线AB在同一铅垂平面内，求汽球离地面的高度（结果保留根号）
22、如图，有两个可以自由转动的转盘A、B，转盘A被均匀地分成4等份，每份分别标上1、2、3、4四个数字；转盘B被均匀地分成6等份，每份分别标上1、2、3、4、5、6六个数字。有人为甲、乙两人设计了一个游戏，其规则如下：
（1） 同时自由转动转盘A与B；
（2） 转盘停止后，指针各指向一个数字（如果指针恰好指在分格线上，那么重转一次，直到指针指向某一数字为止），用所指的两个数字作乘积，如果得到的积是偶数，那么甲胜；如果得到的积是奇数，那么乙胜（如转盘A指针指向3，转盘B指针指向5，3×5=15，按规则乙胜）。
你认为这样的规则是否公平？请说明理由.
(A) (B)
| 得分 | 评卷人 |
五、（本题8分）
23、某商店四月份的营业额为40万元，五月份的营业额比四月份有所增长，六月份比五月份又增加了5个百分点，即增加了5%，营业额达到了50.6万元。求五月份增长的百分率。
| 得分 | 评卷人 |
六、（每题8分，共16分）
24、已知：CD为一幅3米高的温室，其南面窗户的底框G距地面1米，CD在地面上留下的最大影长CF为2米，现欲在距C点7米的正南方A点处建一幢12米高的楼房AB（设A、C、F在同一水平线上）
（1） 比较准确地作出高楼AB的影长AE
（2） 问若大楼建成后是否影响温室CD的采光，试通过计算说明理由。
|
|
|
|
|
|
|
25、在学习测量物体的高度这一节内容时，学校数学应用实践小组打算测量学校旗杆的高度。现有以下测量工具：①皮尺一根 ②教学用三角板一副 ③长为2.5 m的标杆一根 ④高度为1.5m的测倾器一架。
请你为他们设计两种测量方案。要求：画出示意图，选择测量工具，并用测出数据（长度用m、n…表示，角度用а、β…表示）表示出旗杆的高AB。
方案一：1、测量工具：
2、在图1中画出示意图
3、计算：AB=
（图1）
方案二：1、测量工具：
2、在图2中画出示意图
3、计算：AB=
（图2）
| 得分 | 评卷人 |
七、（每题7分共14分）
26、阅读下列材料：
有一些几何图形可以被某条直线分成面积相等的两部分，我们将“把一个几何图形分成面积相等的两部分的直线叫做该图形的二分线”，如：圆的直径所在的直线是圆的“二分线”。
解决下列问题：
（1） 三角形的“二分线”可以是
（2） 
在下图中，试用两种不同的方法分别画出等腰梯形ABCD的“二分线”，并说明你的画法。
27、某厂从2001年起开始投入技术改进资金，经技术改进后，其产品的生产成本不断降低，具体数据如下表：
| 年度 | 2001 | 2002 | 2003 | 2004 |
| 投入技改资金x(万元) | 2.5 | 3 | 4 | 4.5 |
| 产品成本y（万元/件） | 7.2 | 6 | 4.5 | 4 |
(1) 请你认真分析表中数据，从你所学习过的一次函数、二次函数和反比例函数中确定哪种函数能表示其变化规律，并求出它的关系式。
(2) 按照这种变化规律，若2005年已投入技改资金5万元。
① 预计生产成本每件比2004年降低多少万元？
② 如果打算在2005年把每件产品成本降低到3.2万元，则还需投入技改资金多少万元（结果精确到0.01万元）？
| 得分 | 评卷人 |
八、（本题12分）
28、在△ABC中，∠B=90º，AB=8cm,BC=4cm，D、E、F分别为AB、AC边上的中点，若P为AB边上的一个动点，PQ⊥AC，交AC于Q，以PQ为一边，在点A的异侧作正方形PQMN，记正方形PQMN与矩形EDBF的公共部分的面积为y.
(1) 如图，当AP=3cm时，求y的值。
(2) 设AP=xcm，试用含x(cm)的代数式表示y(cm2)
(3) 
|
|
|
|
|
|
|
|
当y=2 cm2时，试确定点P的位置。
2005年度第一学期初三第三次联考数学试卷参考答案及评分标准
一、选择（1-12）
B、B、D、C、C、B、D、C、D、A、B、C
二、填空
13、1（4…） 14、y=
(-2…) 15、会
16、1：2
三、17、2cos60°+2sin30°+4tan45° 18、2x2+4x-3=0
解原式=1+1+4……………3分 解：b2-4ac=16+24=40>0………2分
=6…………………6分
∴x=
……………………5分
∴x1=
,x2=
… 6分
19、角平分线………………3分,垂直平分线………………2分
标出P点………………1分
20、(1) ∵ DF∥BE
∴ ∠DFA=∠BEC
又 ∵ AF=CE DF=BE
∴ △AFD≌△CEB……………………………………………3分
（2）∵ △AFD≌△CEB
∴ AD=CB
∠DAF=∠BCF
∴ AD∥CB
∴ 四边形ABCD是平行四边形……………………………3分
21、 解：过C作CD⊥AB，垂足为D…………………1分
设CD=xm
在Rt△ACD中，∠A=45°
∴ AD=CD=xm…………………………………2分
在Rt△BCD中,tan60°=
即=
∴BD=
x……………………………………4分
∵ AD-BD=AB
∴ x-x=20
∴ x=30+10………………………………6分
答：汽球离地面的高度为（30+10）m………… …7分
22、解：列表
|
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 |
B A由表可知：P偶=
，P奇=
………………………………………………5分
∵ > ∴
这样的规则不公平………………………7分
23、解设五月份增长率为x……………………………………………… 1分
40（1+x）(1+x+5%)=50.6……………………………………………4分
解得x1=0.1,x2=-2.15(舍去) …………………………………… 7分
答：五月份增长的百分率为10%。…………………………………8分
|
|
|
|
|
|
|
|
(2) ∵Rt△ABE∽Rt△DCF则
=
即 
=
∴AE=8 ∴CE=1 …………………………………………………………4分
同理：
=即
= ∴HC=1.5m…………………………………… 6分
∵1.5m>1m 即CH>CG
∴温室CD的采光受影响。…………………………………………… …8分
25、方案一：1、工具 ① ④……………………………………………………1分
2、示意图
3、AB=atanа+1.5……………………………………………………4分
方案二：1、工具 ① ②……………………………………………………… 5分
2、示意图
3、AB=a+h……………………………………………8分
(其它方法参照给分)
26、（1）三角形一边中线所在的直线…………………………………………2分
（2）
取上、下底的中点，过两点作直线得梯形的二分线………………4分
过A、D作AE⊥BC，DF⊥BC，垂足E、F，连接AF、DE相交于O，过点O任意作直线即为梯形的二分线（其它方法参照给分）………………………………………7分
27、（1）设其为反比例函数，关系式为y=
………………………………………1分
当x=2.5时，y=7.2,可得k=18,则y=
…………………………………2分
验证：当x=3时，y=6,当x=4时，y=4.5,x=4.5时，y=4
所以，可用y=表示其规律…………………………………… ３分
（２）解① 当x=5万元时，y=3.6
4-3.6=0.4(万元)
所以生产成本每件比２００４年降低０.4万元。……………５分
② 当y=3.2时，x=5.625
因为5.625-5=0.625≈0.63(万元)
所以还需投入０.6万元。………………………………………７分
２８、解（1）由题意可知：ED=BC=2cm，EF=AB=4cm，AD=BD=4cm
当AP=3cm则PD=1cm
由△AQP∽△ACP得，QP= 则PN=MN=
∴y=DN•MN=×=………………………………………………4分
（2）①当0≤x≤
时，y=0……………………………… ……………5分
②当< x≤4时,MN=PN=QP=AP=x
y=(x-4)
= x2-2x……………………………………………8分
③当4< x≤
时，PB=QP=AP=x
y=PQ•BF=x•2=x……………………………………………… 9分
④当< x≤8时，PB=8-x
y=2PB=16-2x………………………………………………… 10分
(四种情况只要能写出函数关系式就给满分)
(3)当y=2时①不符合
把y=2代入②，y=x2-2x得，x1=
,x2=(舍去)
把y=2代入③得x=2,因为2<4,所以不合题意，舍去。
把y=2代入④得x=7。
所以当x=或7时，y=2cm2. ……………………………12分