初三年级第一次模拟考试（数学）
温馨提示：同学们，以下试题是检测你近几年来在科学课上学会的知识、掌握的方法和形成的能力。请别紧张，只要你仔细审题、认真答题，聪明的你一定会交出一份满意的答卷！祝你考试成功！
卷Ⅰ（选择题，共20分）
一、 选择题:（本大题共10个小题，每小题4分，共40分）
1. 计算-2+1的结果是 （ ）
A．-3 B．-1 C．1 D．3
2．以下五家银行行标中，既是中心对称图形又是轴对称图形的有 （ ）
A．4个 B.3个 C.2个 D.1个
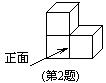
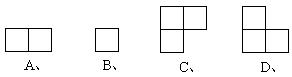
3．如右图，由三个小立方体搭成的几何体的俯视图是 （ ）
4．若点（-5，y1）、(-3,y2)、(3,y3)都在反比例函数y= - 的图像上，则 （ ）
A．y1＞y2＞y3 B．y3＞y1＞y2
C．y2＞y1＞y3 D．y1＞y3＞y2
5．泽雅水库在3月1日到3月10日下闸蓄水期间，水库水位由106米升至135米，假设水库水位匀速上升，那么下列图象中，能正确反映这10天水位h（米）随时间t（天）变化的是 （ ）
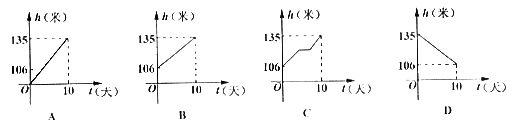
6．设有12只型号相同的杯子，其中一等品7只，二等品3只，三等品2只，则从中任取一只，是二等品的概率等于 （ ）
A. 
B.
C. 
D.
7．在相同时刻的物高与影长成比例。如果高为1.5米的测竿的影长为2.5米，那么影长为30米的旗杆的高是 （ ）
A. 20米 B. 15米 C. 16米 D. 18米
8.若
，则
的值是
（ ）
A．3 B. 
C. -3 D. 
9.如图AB为⊙O一固定直径，自上半园上一点C作弦CD⊥AB，∠OCD平分线交⊙O于P，当点C在上半园上移动时（不包括AB两点），点P
（ ）
A.到CD距离不变 B.位置不变
C.平分弧BD D.平分弧AB
10.根据下列表格的对应值：
| x | 3.23 | 3.24 | 3.25 | 3.26 |
|
| －0.06 | －0.02 | 0.03 | 0.09 |
判断方程
(a≠0，a，b，c为常数)一个解x的范围是 （ ）
A、3＜x＜3.23 B、3.23＜x＜3.24
C、3.24＜x＜3.25 D、3.25 ＜x＜3.26
二、填空题：（本大题共6个小题；每小题5分，共30分．）
11．在函数y=
中自变量x的取值范围是____________.
12．分解因式 ：x3－4x=___________________.
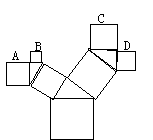
13．如图是一个艺术窗的一部分，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大正方形的边长为5cm，则正方形A、B、C、D的面积和是 ．
14．在Rt△ABC中，∠C＝90°，a=3,b＝4, 则斜边上的中线长为
|
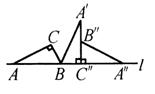
线l上，按顺时针方向在l上转动两次，使它转到
△
A"B"C"的位置．设BC＝1，
，则顶
点A运动到点A"的位置时，点A经过的路线与直
线l所围成的面积是________．（计算结果不取近似值）
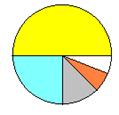
16. 如图是一张面积为1的圆形纸片，依次用不同色彩填涂圆面积的
，根据图形变化规律推断：当n为正整数时，
.
三.解答题：(本大题共8个小题；第17到20题每题8分，第21题10分，第22，23题每题12分，第24题14分，共80分．)
17.计算：（1）
（2）解不等式：
18．已知：如图，梯形ABCD中，
，E是BC的中点，直线AE交DC的延长线于点F。
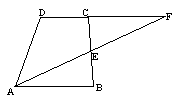求证：△ABE≌△FCE；
19.小芳在为班级办黑板报时遇到了一个难题，在版面设计过程中需将一个半圆面的面积三等分。如图，请你帮助她设计一个合理的等分方案．要求用尺规作出图形，保留作图痕迹.
 |
20.如图是某汽车行驶的路程S (km)与时间t (min)的函数关系图.观察图中所提供的信息，解答下列问题：
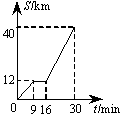（1）汽车在前9分钟内的平均速度是多少？
（2）汽车在中途停了多长时间？
（3）当16≤t≤30时，求S与t的函数关系式.
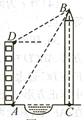21、如图，小丽家住在成都市锦江河畔的电梯公寓AD内，她家河对岸新建了一座大厦BC，为了测得大厦的高度，小丽在她家的楼底A处测得大厦顶部B的仰角为60°，爬上楼顶D处测得大顶部B的仰角为30°，已知小丽所住的电梯公寓高82米，请你帮助小丽算出大厦高度BC及大厦与小丽所住电梯公寓间的距离AC。
22． 某手机生产厂家根据其产品在市场上的销售情况，决定对原来以每部2000元出售的一款彩屏手机进行调价，并按新单价的八折优惠出售，结果每部手机仍可获得实际销售价的20%的利润（利润=销售价—成本价）.已知该款手机每部成本价是原销售单价的60%.
（1）求调整后这款彩屏手机的新单价是每部多少元？让利后的实际销售价是每部多少元？
（2）为使今年按新单价让利销售的利润不低于20万元，今年至少应销售这款彩屏手机多少部？
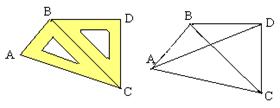23. 将一副三角尺如图摆放一起,连接AD,试求∠ADB的正切值。
24. 数学课上，老师出示如图和下面框中的条件：
 | |||
 | |||
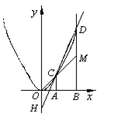小明发现两个结论：
① S△CMD∶S梯形ABMC＝2∶3；
② 数值相等关系：xC·xD＝-yH．
(1) 请你验证结论①和②成立；
(2) 请你研究：如果将上述的条件“A点坐标(1，0)”改为“A点坐标(t，0)(t＞0)”，其它条件不变，结论①是否仍成立？(请说明理由)
(3) 进一步研究：如果将上述框中的条件“A点坐标(1，0)改为A点坐标(t，0)(t＞0)”，又将条件“y＝x2 ”改为“y＝ax2(a＞0)”，其它条件不变，那么xC，xD和yH有怎样的数值关系？(写出结果并说明理由)