初三趣味数学练习卷

初三趣味数学练习卷 　　

学校　　　　 　 班级　　　 　 姓名　　　 　 得分　　　

一、选择题（每小题5分，共30分）

1.关于x的方程x²+kx+k²-9=0只有一个正根，那么k的值是(　 )

A．k＞3或＜-3　　　　　　　  B.k=±3

C.k≥3或k≤-3　　　　　　　  D.-3≤k＜3

2．代数式 的化简结果是（　　）

A． 　　　　B. 　　　　　 C. 　　　　D.

3．已知b²-4ac是一元二次方程ax²+bx+c=0(a≠0)的一个实数根，则ab的取值范围为（　　）

A．  　　　B．　　　 C． 　　 D．

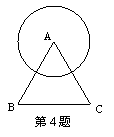
4. 如图，⊙A的直径等于等边△ABC的边长，等腰

△AB^/C^/的周长与△ABC的周长相同，且B^/C^/与⊙A

相切，那么 （　　）

　　A．∠B^/AC^/＞120°　　B．∠B^/AC^/=120°

 C．∠B^/AC^/＜120°　　D. ∠B^/AC^/与120°的大小无关

5．一元二次方程中，若a,b都是偶数，c是奇数，　　则这个方程（　　　　）

A．有整数根　　B．没有整数根　　 C．没有有理数根　　 D．没有实数根

6．一个三角形的三边长分别为a、a、b，另一个三角形的三边长分别为a、b、b，其中a＞b.若两个三角形的最小内角相等，则的值等于（　　）

A．B．C．D．

二、填空题（每小题5分，共30分）

D(0,2)

7.如图，⊙C通过原点，并与坐标轴分别交于A,D两点，已知∠OBA=，点D的坐标为(0,2)，则点A,C的坐标分别为__________________ .

O

8．若x²+xy+y=14，y²+xy+x=28，则x+y=________.

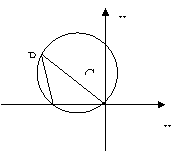
9.已知关于的不等式组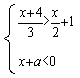的解集为，那么a的取值范围是________.　　　　　　　

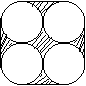
10.如图，图中4个圆的半径都为a，那么阴影部分的面积为________.　　　　　　　

11.设、是方程的两个实根，且．则的值是　　　　　　　　　　　 .

12. 设等式在实数范围内成立，其中a、x、y是两两不同的实数，则的值是 ________.

三、解答题（每题15分，共60分）

13.某班参加一次智力竞赛，共a,b,c三道题，每题或者得满分或者得0分，其中题a满分20，b，c题满分分别为25分，竞赛结果，每个学生至少答对了一题，三题全答对的有1人，答对其中两道题的有15人，答对题a的人数与答对题b的人数之和为29；答对题a的人数与答对题c的人数之和为25；答对题b的人数与答对题c的人数之和为20，问这个班的平均成绩是多少？

14.已知关于x的方程x²-(6-a) x+a=0的两根都是整数，求a的值．

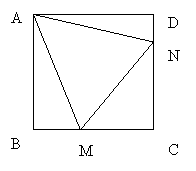15. 如图，点M,N分别在正方形ABCD的边BC,CD上，已知△MCN的周长等于正方形ABCD周长的一半，求∠MAN的度数.

　

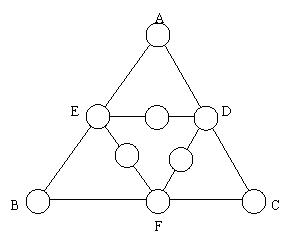16．把数字1，2，3，…，9分别填入右图的9个圈内，要求三角形ABC和三角形DEF的每条边上三个圈内数位之和等于18.

（1）给出符合要求的填法

（2）共有多少种不同填法？证明你的结论

初三趣味数学练习卷（二）答案

一、选择题

1．D 2．C 3．C 设，则得方程或，由，得

4. C（设⊙A的半径为R，△ABC的周长为6R，作切线与⊙A相切与点D，又点A为顶点，作一顶角为120度，且以切线段B^/C^/ 为底边的等腰△AB^/C^/，连结AD，则AD⊥B^/C^/，则得等腰△AB^/C^/的周长是＞6R）

5.B 6．B,作△ABC，其中∠A=36°AB=AC=a，BC=b，作∠BCA平分线，则AD=DC=b，AC=a，△ABC∽△CBD,由，得，解得

二、填空题

7.A 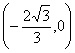C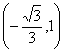,连AC,CO,△ACO为正三角形　8．-7或6两方程相加，得 9．

10. 连AD,BC,CD，则S_阴影是由ABCD围成阴影面积的6倍，为12a²-3 a²　

11．1　利用韦达定理 　 12．由条件：x=y=a＞0，3；

三、解答题

13.设分别表示答对题a,题b,题c的人数，则有x_a+x_b=29,x_a+x_c=25,x_b+x_c=20, x_a=17　

x_b =12,x_c=8,答对一题的人数为，全班人数为1+4+15=20，故全班平均成绩为（分）

14．解 设两个根为x₁≥x₂，由韦达定理得

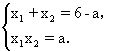
　　从上面两式中消去a得

x₁x₂+x₁+x₂＝6，

　　所以 (x₁＋1)(x₂+1)=7，

　　

　　　

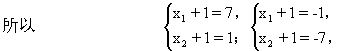
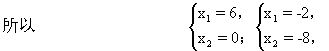
　　所以a=x₁x₂=0或16

15．延长CB至G，使BG=DF，连结AG，则△ABG≌△ADF,AG=AF,∠BAG=∠DAF=15^O, ∠GAE=∠FAE=45^O, △GEA≌△FAE,EF=EG, ∠AEF=∠AEG=60^O

在Rt△ABE中,AB=,∠BAE=30^O,CE=-1,在Rt△EFC中,

∠EFC=30^O,EF=2(-1),故S_△FAE=S_△AEG=1/2EG*AB=3-.

　　

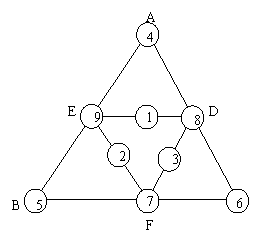16．（1）右图给出了一个符合要求的填法；　

（2）共有6种不同填法

把填入A,B,C三处圈内的三个数之和记　为x；D,E,F三处圈内的三个数之和记为y；其余　　三个圈所填的数位之和为z.显然有x+y+z=1+2+…+9=45　 ①

图中六条边，每条边上三个圈中之数的和　

为18，所以有

z+3y+2x=6×18=108　　 ②

②-①,得

X+2y=108-45=63　　　　③

把AB,BC,CA每一边上三个圈中的数的和　

相加，则可得