初三数学第一学期期中试卷
一、选择题(每小题2分，共20分)
1．方程
的解是 （ ）
（A） 
（B） 
（C） 
（D） 或3
2．方程
的左边配成完全平方后所得方程为 （ ）
（A） 
（B） 
（C） 
（D） 
3．下列方程中，有两个相等的实数根的方程是 （ ）
（A） 
（B） 
（C） 
（D） 
4．某厂生产一种药品，原来每瓶的成本是100元，由于提高生产过程的科技含量，连续两次降低成本，现在的成本是81元.则平均每次降低成本 （ ）
（A） 8.5％ （B） 9％ （C） 9.5％ （D） 10％
5．下列命题中,真命题是 （ ）
(A) 对角线相等的四边形是矩形 (B) 相似三角形一定是全等三角形
(C) 等腰三角形底边上的中线与底边上的高重合 (D) 等腰三角形一定是中心对称图形
6．二次函数
配方成
的形式后得 （ ）
（A） 
（B） 
（C） 
（D） 
7．已知抛物线
过(1，－1)、(2，－4)和(0，4)三点，
那么a、b、c的值分别是（ ）
（A）a＝－1，b＝－6，c＝4 （B）a＝1， b＝－6，c＝－4
（C）a＝－1，b＝－6，c＝－4 （D）a＝1， b＝－6，c＝4
8．函数
的图象的顶点坐标是(3，2)，
则这个二次函数的函数关系式是 （ ）
（A）
（B） 
（C）
（D） 
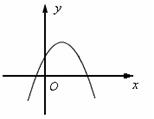9．二次函数的图象如图所示，下列结论正确的是（ ）
（A）a＞0，b＞0，c＞0
（B）a＜0，b＜0，c＞0
（C）a＜0，b＞0，c＜0
（D）a＜0，b＞0，c＞0
10．若一元二次方程ax2+bx+c＝0的两根为x1＝－3，x2＝1，
则二次函数y=ax2+bx+c图象的对称轴是 （ ）
（A） 直线x = 1 （B） y轴 （C） 直线x = －1 （D） 直线x = －2
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题（每空2分，共20分）
11．关于
的方程
是一元二次方程，则
的值为 ．
12．关于x的方程x2－mx－2=0的两根互为相反数，那么m值为 ．
13．一个长方形铁片的长是宽的2倍，四角各截去一个边长为5cm的正方形，
然后折起来做一个没盖的盒子，作成的盒子容积为1500cm3，则这个长方形铁片的
长等于 cm，宽等于 cm．
14．“内错角相等，两直线平行”的逆命题是__________________________．
15．二次函数
的图像向下平移1个单位，得到的图像的表达式是 ．
16．已知抛物线
的最大值是0，则m的值是 ．
17．顶点为（－2，－5）且过点（1，－14）的抛物线的解析式为 ．
18．若抛物线
与轴的两个交点为A、B，则线段AB的长度是
．
19．一小球以15m/s的初速度向上竖直弹起．它在空中的高度h (m)与时间t (s)
满足关系式：h＝15 t－5t 2，当t ＝_______s时，小球的高度为10m．
三．解答题（本题有8小题，共60分）
20．如图，矩形ABCD中，点E为BC边的中点，将∠D折起，使点D落在点E处．请你用尺规作图画出折痕和折叠后的图形．（不要求写作法，要保留作图痕迹）（本题5分）
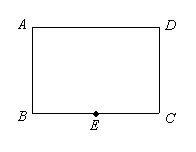
结论：直线 即为折痕，多边形 即为折叠后的图形．
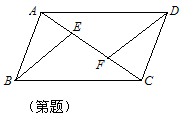
21． 如图，在□ABCD中，E，F是对角线AC上的两点，且AF＝CE．
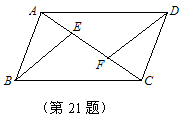求证：BE＝DF．（本题6分）
22．解下列关于方程的问题（共12分）
（1） 解方程
（4分） （2）解方程 
（4分）
（3）已知关于x的方程
的两个根是0和－3，
求p、 q的值． （4分）
23．关于的方程
有两个不相等的实数根，
（1）求
的取值范围； （3分）
（2）是否存在实数，使方程的两个实数根的倒数和等于零？若存在，求出的值；
若不存在，请说明理由． （3分）
24．阅读材料：为了解方程
，我们可以将
视为一个整体，然后设
，
，
则原方程可化为
①
解得
．
当
时，
，
当
∴原方程的解为：
解答问题：仿造上题解方程：
． （本题6分）
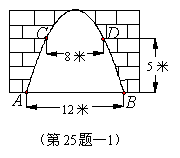
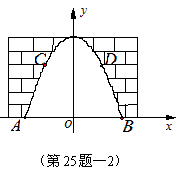25．如图，某地一古城墙门洞呈抛物线形，已知门洞的地面宽度AB＝12米，两侧距地面5米高C、D处各有一盏路灯，两灯间的水平距离CD＝8米，求这个门洞的高度. （提示：选择适当的位置为原点建立直角坐标系，例如下右图：以AB的中点为坐标原点建立直角坐标系.）（本题7分）
26．让我们一起来探究以下问题：
(1) 在同一平面内4条互不重合的直线可能有的交点数为 ．
(在横线上填上正确答案的序号)
①0个；②1个；③2个；④3个；⑤4个；⑥5个；⑦6个；⑧7个．
(2) 设在同一平面内有n条互不重合的直线，它们最多有S个交点(整数n≥2)，
请通过分析，填写下表：
| n | 2 | 3 | 4 | 5 | … |
S | 1 | … |
(3) 请猜想(2)中S与n的函数关系式： ．
(4) 如果平面内若干条互不重合的直线最多有55个交点，求直线的条数．（本题10分）
27．某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利40元，为了扩大销售，
增加赢利，商场决定采取适当的降价措施，经调查发现，如果每件衬衫降低1元，
商场平均每天可多售出2件．
(1) 若为了尽快减少库存，且每天要赢利1200元，每件衬衫应降价多少元？
(2) 若要获得最大利润，每件衬衫应降价多少元？最大利润是多少元？（本题8分）
附加题：(本题10分)（A制班、双语班必做）
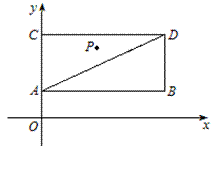
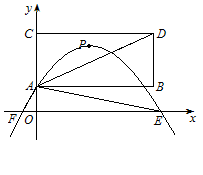
如图，已知A（0，1）、D（4，3），P是以AD为对角线的矩形ABDC内部（不在各边上）的一个动点，点C在
轴上，抛物线
以P为顶点.
（1）能否判断抛物线的开口方向？请说明理由．
（2）设抛物线与轴有交点F、E（F在E的左侧），△E AO与△FAO的面积之差为3，且这条抛物线与线段AD有一个交点的横坐标为
，这时能确定a、b的值吗？若能，请求出a、b的值；若不能，请确定a、b的取值范围.（本题的图形仅供分析参考用）
出卷人：许晓岚 审校人：陈亚霞
初三数学第一学期期中试卷答案
一、选择题(每小题2分，共20分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | A | B | D | C | D | D | A | D | C |
二、填空题（每空2分，共20分）
11．
－2； 12． 0； 13． 40，20； 14． 两直线平行，内错角相等； 15． 
；
16． 2； 17． 
； 18． 2； 19． 1或2．
三．解答题（本题有小题，共分）
20．评分标准：方法正确，但图形有明显误差，得2分；完全正确得3分．结论每空1分．
21．证明：∵□ABCD 中 AB∥CD且AB=CD…………………（2分）
∴∠BAE =∠CDF…………………（1分）
∵AF=CE∴AF+EF=CE+EF∴AE=CF…………………（1分）
在△ABE和△CDF 中
∵ AB=CD，∠ABE =∠CDF，AE=CF
∴ △ABE ≌ △CDF …………………（1分）
∴ BE=DF．…………………（1分）
22．(1)x1＝4，x2＝0；(2) x1＝－1，x2＝
；(3)p＝3，q＝0．
23．(1)∵方程有两个不相等的实数根∴△＞0且k≠0…1分
∴
；…2分(2)假设存在这样的k，x1＋x2＝
，x1x2＝
，…1分
，∴k＝－1，…1分
∵，∴不存在实数，使方程的两个实数根的倒数和等于零．…1分
24．设
，则原方程可化为
…1分 解得
…2分 当
时，
…1分 当
…1分
∴原方程的解为：
…1分
25．由题意可知各点的坐标，A(－6，0)，B(6，0)，C(－4，5)，D(4，5)，由于顶点在y轴，可设抛物线的解析式为
， 将点A(－6，0)，D(4，5)的坐标代入，得方程组 
（2分）解得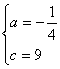
，
（2分）∴门洞的高度是9米（2分）
26．(1)①②④⑤⑥⑦；(2分) (2)3,6,10；(3分)
(3)
；(2分)
(4)11；(3分)
27．(1)设应降价x元，由题意得：(40－2x)(20＋2x)＝1200，解得：x1＝10，x2＝20，但为了尽快减少库存，∴应降价20元；(2) 设降价x元，利润为y元，则y＝(40－2x)(20＋2x)，
当x＝15时，y最大值＝1250，∴应降价15元，最大利润是1250元．
附加题：（1）设顶点P的坐标为（，），则它只能是抛物线的最高点或最低点…（1分）
由题意知：1＜＜3，且经过点A（0，1），所以点P的位置高于点A，说明点P不是抛物线的最低点，所以，点P是抛物线的最高点. …（2分）
由此可判断：抛物线的开口向下. ……（1分）
（2）如图，设抛物线与轴的交点坐标为F（
，0）、E（
，0），则＜0，＞0
S△AEO=OE•OA= ；
S△AFO=OF•OA=
…………（1分）
∵S△AEO－S△AFO = 3 ∴ －（）=3 ，即+=6
∵+=
+
=
∴ = 6 ，即
…① …（1分）
另一方面，设直线AD的解析式为
，并把点A（0，1）、D（4，3）的坐标代入解析式得
，解得
，∴ 
…………（1分）
由于抛物线与线段AD有一个交点的横坐标为，所以纵坐标=
把点（，
）的坐标代入，
整理得
…② …（2分）解由①②组成的方程组得 
，
…（1分）