28.1 锐角三角函数综合训练
（检测时间：60分钟 满分：100分）
班级_______ 姓名_______ 得分_______
一、选择题（每题3分，共24分）
1．计算2sin60°+3tan30°的值为（ ）
A．
B．2 C．3
D．4
2．在Rt△ABC中，各边的长度都扩大4倍，那么锐角B的正切值（ ）
A．扩大4倍 B．扩大2倍 C．保持不变 D．缩小4倍
3．已知α为锐角，tanα=，则cosα等于（ ）
A．
B．
C．
D．
4．如果等腰三角形的底角为30°，腰长为6cm，那么这个三角形的面积为（ ）
A．4.5cm2 B．9cm2 C．18cm2 D．36cm2
5．Rt△ABC中，∠C=90°，b=5cm，a=12cm，则cosB等于（ ）
A．
B．cm
C．
D．cm
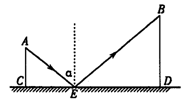
6．如图1所示，CD是平面镜，光线从A点出发经CD上点E，反射后照射到B点，若入射角为α（入射角等于反射角），AC⊥CD，BD⊥CD，垂足分别为C、D，且AC=3，BD=6，CD=11，则tanα的值为（ ）
A．
(1) (2) (3)
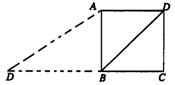
7．如图2所示，已知正方形ABCD的边长为2，如果将线段BD绕着点B旋转后，点D落在CB的延长线上的D′处，那么tan∠BAD′等于（ ）
A．1 B．
C． D．2
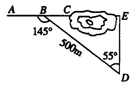
8．如图3，沿AC方向开山修路，为了加快施工进度，要在小山的另一边同时施工，从AC上的一点B，取∠ABD=145°，BD=500m，∠D=55°，要使A，C，E成一直线，那么开挖点E离点D的距离是（ ）
A．500sin55°m B．500cos55°m
C．500tan55°m D．500cot55°m
二、填空题（每题3分，共21分）
9．在△ABC中，若│sinA-1│+（-cosB）2=0，则∠C的度数是______．
10．在Rt△ABC中，∠A是锐角，则│-sinA│+
=______．
11．在△ABC中，∠A=90°，设∠B=θ，AC=b，则AB=_____．（用b和θ的三角比表示）
12．若tan（x+20°）=，则x=_____．
13．锐角α越大，则tanα越_______．（填“大”或“小”）
14．等腰三角形△ABC中，AB=AC，底边BC=10，S△ABC=
，那么∠A=_____，∠B=______．
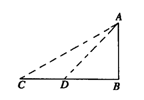
15．如图所示，在C处测得铁塔AB的塔顶A的仰角为30°，向塔前进10m到达D，在D处测得A的仰角为45°，则铁塔的高为________．
三、解答题（55分）
16．（8分）计算．
（1）2cos60°-
sin45°sin60° （2）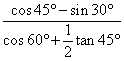
17．（6分）已知α为锐角，当
无意义时，求sin（α+15°）+cos（α-15°）的值．
18．（6分）求2sin2α-3sinα+3=0中锐角α的值．
19．（11分）已知：如图，在△ABC中，∠C=90°，CD是高，BC=10cm，∠B=53°6′，求CD、AC、AB．（精确到1cm）
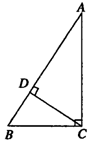
20．（12分）如图所示，等腰梯形ABCD，AD∥BC，∠DBC=45°，翻折梯形ABCD，使点B重合于点D，折痕分别交边AB、BC于点F、E，若AD=2，BC=8．
求：（1）BE的长；（2）∠COE的正切值．
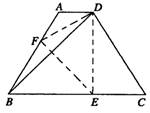
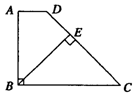
21．（2006，北京）（12分）已知：如图，在梯形ABCD中，AD∥BC，∠ABC=90°，∠C=45°，BE⊥CD于点E，AD=1，CD=2．求：BE的长．
答案:
1．B 2．C 3．A 4．B 5．C 6．C 7．B 8．B
9．60° 10．1 11．cot 12．10° 13．大
14．120° 30° 15．5（+1）m
16．（1）-；（2）- 17． 18．α=60°
19．CD=BC·sinB=10·sin53°6′≈8（cm），
AC=BC·tanB=10·tan53°6′=13（cm），
AB=
≈17（cm）
20．（1）由题意知BE=DE，EF⊥BD，∠DBE=∠BDE=45°，
∴BD⊥BE，根据等腰梯形性质易求EC=3，∴BE=5
（2）tan∠CDE=
=
21．解：过点D作DF∥AB交BC于点F，
∵AD∥BC，
∴四边形ABFD是平行四边形，
∴BF=AD=1，
由DF∥AB，得∠DFC=∠ABC=90°，
在Rt△DFC中，∠C=45°，CD=2，
由cosC=
，求得CF=2，
∴BC=BF+FC=3，
在△BEC中，∠BEC=90°，sinC=
，求得BE=
．