圆24.1练习卷
一． 选择题
1. 下面四个命题中正确的是（ ）
Ａ．平分一条直径的弦必垂直于这条直径
Ｂ．平分一条弧的直线垂直于这条弧所对的弦
Ｃ．弦的垂线必过这条弦所作圆的圆心
Ｄ．在一个圆内平分一条弧和它所对弦的直线必过这个圆的圆心
2.过⊙O内一点Ｍ的最长弦为4㎝，最短弦为2㎝，则ＯＭ的长为( )
A. 
㎝ B. 
㎝ Ｃ．1㎝ Ｄ．3㎝
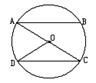3．在⊙O中，如果弦AB所对的圆心角为70°，那么劣弧AB所对的圆周角是（ ）
A．140° B．70° C．35° D．145°
4．如图：AC是⊙O的直径，AB，CD是⊙O的两条弦，且AB∥CD．如果∠BAC=32°，则∠AOD=（ ）
A．16° B．32° C．48° D．64°
5．在同圆或等圆中，如果圆心角∠ＢＯＡ等于另一个圆心角∠ＣＯＤ的2倍，则下列式子中能成立的是（ ）
Ａ．ＡＢ＝２ＣＤ Ｂ．
＝2
Ｃ．＜2 Ｄ．＝
6．在同圆或等圆中，如果＝2
，则ＡＢ和ＣＤ的关系是（ ）
A.＞2 B.AB＝2CD
C.AB＜2CD D.AB=CD
7．下列语句中,正确的个数是( )个.
①相等的圆心角所对的弧相等；
②同圆或等圆中，相等的圆周角所对的弦相等；
③一边上的中线等于这条边一半的三角形是直角三角形；
④等弧所对的圆周角相等；
⑤一条弧所对的圆心角等于它所对的圆周角的一半
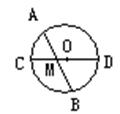
A 2 B 3 C 4 D 5
8．如图，AB是⊙O的直径，M为OB的中点，弦CD经过点M，且
AB＝16㎝，∠CMA＝30o，则CD等于（ ）㎝.
(A) 2
(B)4
(C) 12 (D)
10
二．填空题
1.在⊙O中，弦ＡＢ长为8㎝，圆心到弦ＡＢ的距离为3㎝，则⊙O半径为
2．一弓形弦长为
㎝，弓形所在圆的半径为7㎝，在弓形的高是
3．在半径为5㎝的圆内有两条互相平行的弦，一条弦长为8㎝，另一条弦长为6㎝，则这两条弦之间的距离为
4．已知⊙O的半径为Ｒ，弦ＡＢ的长也为Ｒ，则∠ＡＯＢ＝ ，弦心距为 ，弦ＡＢ所对的圆周角的度数为
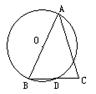5．如图，已知AB是⊙O直径，D是圆上任意一点（不与Ａ点重合），连结BD，并延长到C，使DC=DB，连结AC，则⊿ABC的形状是
6．⊙O中弦ＡＢ是半径ＯＣ的垂直平分线，则∠ＡＯＢ的度数为
7．如图，∠B=∠OAC，OA=8cm,则AC= cm
8．如图，弦CD和直径AB平行，若∠AED＝60°，AB＝6cm，则梯形ABCD的面积为
三．解答题
1．如图，有一座石拱桥的桥拱是以O为圆心，
OA为半径的一段圆弧。若∠AOB=120°，
OA=4米，请求出石拱桥的高度。
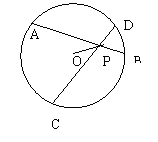
2. 如图，⊙O中，AB与CD相交于P，OP恰好平分∠APC，求证：AB=CD
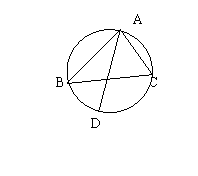3．如图，在⊙O中，△ABC是它的内接三角形，AD是⊙O的直径，∠ABC=40°，求∠CAD的度数.
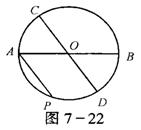4．如图， 已知AB、CD是⊙O的两条直径，AP是⊙O的弦，且AP∥CD，求证
=
5．在⊙O中, 弦AB=24, 弦CD=10, O点到AB的距离为5, 求O点到CD的距离
 |
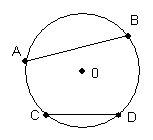6．已知：如图, △ABC是⊙O的内接三角形, 且AB=AC=
,BC=8, 求⊙O的直径长
 |
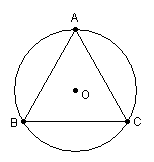7．如图, ⊙O的半径为5, P是⊙O外一点, PO=8, ∠OPA=30°求AB, PB的长．
 |
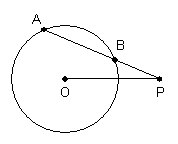8．已知：如图：AB是⊙O的直径，CD是弦，CE⊥CD，DF⊥CD．求证：AE=BF
 |
9、如图，⊙O的半径为6㎝，弦AB＝6㎝，OC⊥AB，垂足为C，以点O为圆心，OC为半径作圆，交OA于D，交OB于E。⑴求小圆半径OC的长。 ⑵求证：OC垂直平分DE。
 | |||
| | |||
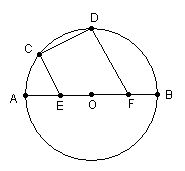
10、如图：AB是的直径，CD是弦，过A、B两点作CD的垂线，垂足分别为E、F，若AB=10，AE=3，BF=5，求EC的长。
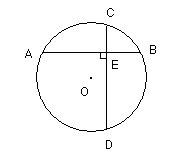11．已知：如图5；⊙O的半径为5，AB、CD为⊙O的两条弦，且AB⊥CD于E，若AE、BE为方程
的两个根，O到AB的距离为3；求：k的值及CD的弦心距.
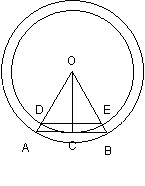
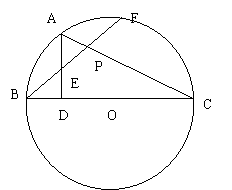12．如图，BC为⊙O的直径，AD⊥BC，垂足为D，A为弧BF的中点，BF和AD交于E，连结AF与AC,AC交BF于P
① 求证：AE=BE ② 求证：AE=PE
③ 若ED:BD=3:4,EP=
,求DC的长