九（下）数学《直线与圆、圆与圆的位置关系》测试卷（附答案）
班级 姓名 得分
一、选择题（每题4分，共40分）
1. ⊙O的直径是3，直线
与⊙0相交，圆心O到直线的距离是d，则d应满足 ( )
A. d>3 B. 1.5<d<3 C. O ≤d<1.5 D.d<O
2. 在平面直角坐标系中，以点（2 , l）为圆心、1为半径的圆必与（ )
A. x轴相交 B.y轴相交 C. x轴相切 D. y轴相切
3. 已知两圆的圆心距是3，两圆的半径分别是方程x2-3x+2=0的两个根，则这两个圆的位置关系是（ )
A．外离 B．外切 C．相交 D．内切
4．已知⊙O1与⊙O2内切，它们的半径分别为2和3，则这两圆的圆心距d满足（ ）
（A）d=5 （B）d=1 （C）1＜d＜5 （D）d ＞5
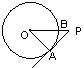5．如图，PA为⊙O的切线，A为切点，
PO交⊙O于点B，PA=3，OA=4，
则cos∠APO的值为（ ）
（A） （B） （C） （D）
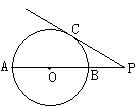
6.如图，AB是⊙O的直径，P是AB延长线上的一点，
PC切⊙O于点C，PC=3、PB：AB=1：3，则⊙O的半
径等于（ ）
A． 
B. 
C. 
D. 
7．已知正三角形的内切圆半径为cm，则它的边长是（ ）
（A）2 cm （B）cm （C）2cm （D）cm
8．已知半径均为1厘米的两圆外切，半径为2厘米，且和这两圆都相切的圆共有（ ）
（A）2个 （B）3个 （C）4个 （D）5个
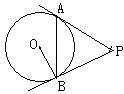
9.如图，AD、AE分别是⊙O的切线，D、E为切点，BC切⊙O于F,交AD、AE于点B、C，若AD=8.则三角形ABC的周长是（ ）
A. 8 B.10 C.16 D.不能确定
10.要在一个矩形纸片上画出半径分别是4cm和1cm的两个外切圆，该矩形面积的最小值是（ ）
A. 36 B. 72 C. 80 D. 100
二、填空题（每小题5分，共30分）
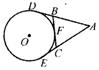
1、如图8，PA、PB是⊙O的切线，A、B为切点，若
∠APB=60°，则∠ABO= .
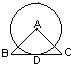2．如图，在△ABC中，∠A=90°，AB=AC=2cm，
⊙A与BC相切于点D，则⊙A的半径为 cm．
3.两圆内切，其中一个圆的半径为5，两圆的圆心
距为2，则另一个圆的半径是 .
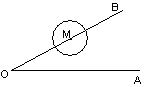4．如图，已知∠AOB=30°，M为
OB边上一点，以M为圆心、2 cm为
半径作⊙M．若点M在OB边上运
动，则当OM= cm时，⊙M
与OA相切．
5．①OC是⊙O的半径；②AB⊥OC；③直线AB切⊙O于点C．请以其中两个语句为条件，一个语句为结论，写出一个真命题 ．
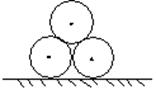6、如图9，施工工地的水平地面上有三根外径都是
1米的水泥管，两两相切地堆放在一起，则其最
高点到地面的距离是 .
三、解答题（共50分）
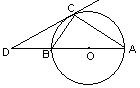1．如图，△ABC中，∠BCA=90°，∠A=30°，以AB为直径画⊙O，延长AB到D，使BD等于⊙O的半径．
求证：CD是⊙O的切线．（8分）
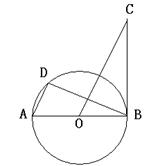
2.（10分）如图，AB是⊙O的直径，BC是⊙O的切线，
D是⊙O上一点，且AD∥OC
（1）求证：△ADB∽△OBC
（2）若AB=2，BC=
，求AD的长（结果保留根号）
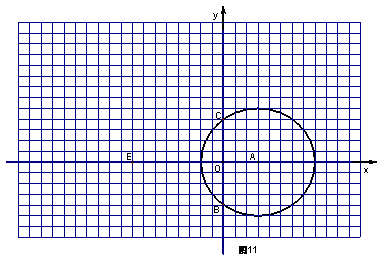
3.（本题12分）正方形网格中，每个小正方形的边长为1个单位，以O为原点建立平面直角坐标系。圆心为A（3，0）的⊙A被圆心为A（3，0）的A被y轴截得的弦长BC＝8，如图11所示。解答下列问题：
（1）⊙A的半径为＿＿＿＿＿；
（2）请在图中将⊙A先向上平移6个单位，再向左平移8个单位得到⊙D，观察你所画的图形知⊙D的圆心D点的坐标是＿＿＿＿＿；⊙D与x轴的位置关系是＿＿＿＿；⊙D与y轴的位置关系是＿＿＿＿＿；⊙D与⊙A的位置关系是＿＿＿＿＿＿＿。
（3）画出以点E（—8，0）为位似中心，将⊙D缩小为原来的
的⊙F
4.（本题8分）如图1，
分别表示边长为
的等边三角形和正方形，
表示直径为的圆．图2是选择基本图形
用尺规画出的图案，
（1）写出图2的阴影部分的面积
（2）请你从图1中任意选择两种基本图形，按给定图形的大小设计一个新图案，还要选择恰当的图形部分涂上阴影，并计算阴影的面积；（尺规作图，不写作法，保留痕迹，作直角时可以使用三角板）
（3）请你写一句在完成本题的过程中感受较深且与数学有关的话．
5.（本题满分12分，）
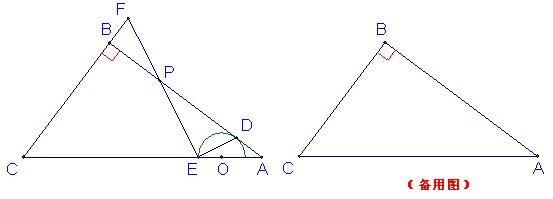
在△ABC中，∠ABC＝90°，AB＝4，BC＝3，O是边AC上的一个动点，以点O为圆心作半圆，与边AB相切于点D，交线段OC于点E，作EP⊥ED，交射线AB于点P，交射线CB于点F。
（1） 如图，求证：△ADE∽△AEP；
（2） 设OA＝x，AP＝y，求y关于x的函数解析式，并写出x的取值范围；
（3） 当BF＝1时，求线段AP的长.
附参考答案：一、CCBBBCADCB
二、（1）30°（2）
（3）7或3 （4）4 （5）①③
②或②③① （6）1+
三、1、提示：连结OC，先证△OBC是等边三角形，再证∠DCB=30°即OC⊥CD
2、（1）∠ADB=∠ABC=90°∠DAB=∠C0B （2）AD=
3、（1）5 （2）（-5，6）相离，相切，外切 （3）略
4、（1）
（2）（3）略
5、（1）连结OD，∠A=∠A，∠ADE=∠AEP（2）
（3）2或6