初三年级数学第一学期期中考试

初三年级数学第一学期期中考试

试卷

一、填空题（每题2分，共38分）

1.人体中成熟的红细胞的平均直径约0.m，用科学记数法表示为　　　　　 m.

2.若分式的值为0，则x＝　　　　 .

3. ＝　　　　　　　 ；＝　　　　　 .

4.若，则x＝　　　　 ；若，，则＝　　　　  .

5.已知关于x的方程有增根，则m＝　　　　  .

6.已知关于x的一元二次方程的一个根是0，则a的值为　　　 .

7.已知关于x的方程的一个根是，则另一根是　　 ，m＝　　　 .

8.一张餐桌的桌面是一个长160cm、宽100cm的长方形，现要设计一块桌布，使得桌布的面积是桌面面积的2倍，且使四周垂下的边等宽，若设四周垂下的边宽为xcm，则应列得方程为　　　　　　　　　　　　　　　　　 .

9.若圆锥的底面半径为6cm，高为8cm，则这个圆锥的侧面积是　　　　 cm².

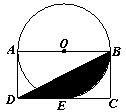
10.如图，在⊙O中，AB是⊙O的直径，∠AOC＝130⁰,则∠D的度数为　　　　.

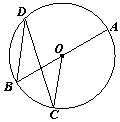
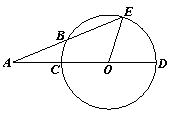
11.如图，CD为⊙O的直径，∠EOD＝69⁰，AE交⊙O于B，且AB＝OC，则∠E＝　　 .

12.⊙O的半径为3,点P是⊙O外一点，OP的长为4,则以点P为圆心，且与⊙O相切的圆的半径为　　　　　　 .

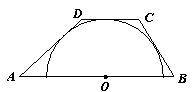
13.如图，半圆O的圆心在梯形ABCD的下底AB上，且另外三边AD、DC、CB均与半圆O相切.已知AD＝4,BC＝3,则AB的长为　　　　　　　　  .

14.已知，如图，矩形ABCD中，BC＝2,DC＝4,以AB为直径的⊙O与DC相切于点E，则阴影部分的面积为　　　　　　　　　　　  .（结果保留）.

　

(第10题)　　　　　 （第11题）　　　　　　  （第13题）　　　　　  （第14题）

15.如图，△ABC是等腰直角三角形，点P为斜边BC上一点，将△ABP绕点A逆时针旋转后能与△ACD重合，若AP＝3,则PD＝　　　　　　　　　　 .

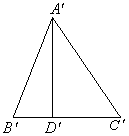
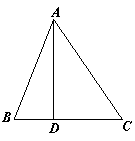
16.如图，AD、分别是△ABC和△中BC、边上的高，且AB＝，

AD＝，若要使△ABC≌△，请你补充条件　　　　　　　　  .

（只需填写一个你认为正确的条件）

　　

　（第15题）　　　　　　　　　　　  （第16题）

二、选择题（每题3分，共18分）

17.给出下列方程①　　②　　③

④，其中是一元二次方程的有　　　　　　　　　　　　　　　　  （　　　）

A.1个　　B.2个　　C.3个　　D.4个

18.将中的a、b都扩大到原来的3倍，则分式的值　　　　　　　　　　 （　　　）

A.不变　　B.扩大到原来的3倍　　C.扩大到原来的6倍　　D.扩大到原来的9倍

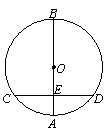
19.如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，若AB＝20，CD＝16,则AE的长为（　　　）

A.4　　B.6　　C.8　　D.10

　　　　　　　　　　　 

（第19题）　　　　　　　　　　　　　　　　　 （第21题）

20.已知等腰△ABC中，AB＝AC＝5,底边BC＝6,若以顶点A为圆心，以4为半径作⊙A，则BC与⊙A　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　　）

A.相交　　B.相切　　C.相离　　D.不能确定

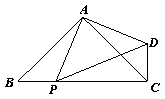
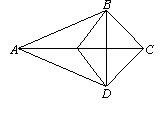
21.如图AB＝AD，BC＝CD，则图中全等的三角形共有　　　　　　　　　　　　  （　　　）

A.4对　　B.5对　　C.6对　　D.7对

22.若关于x的一元二次方程有实数根，则k的取值范围是　　　　（　　  ）

A. 或　　B. 　　C. 　　D. 且.

三、解答题

23.解下列方程：（每题4分，共8分）

⑴　　　　　　　　　　  ⑵

24.⑴（本题4分）计算：

 

⑵（本题4分）已知，求代数式的值.

25.（本题8分）如图，四边形OABC和ODEF均为正方形，CF交OA于点P，交DA于点Q.

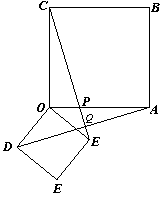⑴求证：AD＝CF；

⑵猜想AD与CF的位置关系，并给出证明.

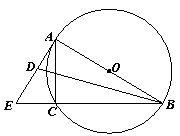26.（本题10分）已知，如图，AB是⊙O的直径，⊙O的切线EA与弦BC的延长线相交于点E，∠EBA的平分线交EA于点D，∠ABC＝30⁰.

⑴求∠ADB的度数；

⑵若EA＝4cm,求BC的长.

27.（本题8分）江阴青年旅行社为吸引广大市民组团去天目湖风景区旅游，推出了如下收费标准：

标准1：如果人数不超过25人，人均旅游费用为1000元；

标准2：如果人数超过25人，每增加1人，人均旅游费用降低20元，但人均旅游费用不得低于700元.

某单位组织员工去天目湖风景区旅游，共支付给青年旅社旅游费用27000元，请问该单位这次共有多少员工去天目湖风景区旅游？

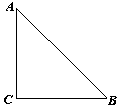
28.（本题8分）在一个玩具厂里有大量边角布料，现找出其中的一种形状为等腰直角三角形的面料（如图），测量得∠C＝90⁰，AC＝BC＝8.现在要从这种等腰直角三角形中剪出一种扇形用来做成不同形状的玩具，要求使扇形的两条边缘半径恰好都在△ABC的边上，且扇形的弧与△ABC的其他边相切.请你设计出所有可能符合题意的方案示意图（只要求画出扇形），并直接写出扇形的半径.（注：备用图不够可以自己添加图形.）

　　 　　　　

29.（本题12分）已知，如图，在△ABC中，AB＝6cm，BC＝8cm,∠B＝90⁰,点P从A点开始沿AB边向点B以1cm/s的速度移动，点Q从B点开始沿BC边向点C以2cm/s的速度移动.

⑴若P、Q分别从A、B同时出发，经几秒钟，△PBQ的面积为8cm²？

⑵若P、Q分别从A、B同时出发，并且P到B后又继续在BC边上前进，Q到C后又继续在CA边上前进，经几秒钟，△PCQ的面积为12.6cm²?

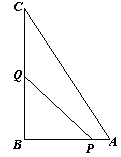
30.（本题12分）已知Rt△ABC中，∠ACB＝90⁰，AC＝6,BC＝8.

⑴如图①，若半径为r₁的⊙O₁是Rt△ABC的内切圆，求r₁；

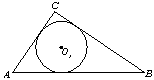　　　　图①

⑵如图②，若半径为r₂的两个等圆⊙O₁、⊙O₂外切,且⊙O₁与AC、AB相切，⊙O₂与BC、AB相切，求r₂；

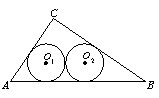
　　　 图②

⑶如图③，当n是大于2的正整数时，若半径为r_n的n个等圆⊙O₁、⊙O₂、……、⊙O_n依次外切,且⊙O₁与AC、AB相切，⊙O_n与BC、AB相切，⊙O₂、⊙O₃……、⊙O_n-1均与AB边相切，求r_n.

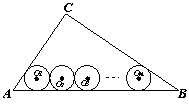　　　　  图③