初三数学第一学期期中学业能力测试
班级： 姓名： 得分：
一. 仔细选一选 (本题有10个小题, 每小题3分, 共30分)
下面每小题给出的四个选项中, 只有一个是正确的, 请把正确选项前的字母填在
答题卷中相应的格子内. 注意可以用多种不同的方法来选取正确答案.
1、下列各问题情景中均包含一对变量，试判断那对变量是成反比例的（ ）
A、圆的周长
和圆的半径
B、在压力不变的情况下，压强P和支承面的面积S
C、
中，y与x成反比例关系
D、玉华初级中学的男生人数
和女生人数
2、下列函数中，属于二次函数的是（ ）
3、反比例函数
的图象位于( )
A、第一、二象限 B、第一、三象限 C、第二、三象限 D 、第二、四象限
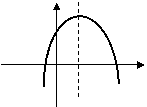4、已知二次函数的图象如右图，则
满足（ ）
5、
（ ）
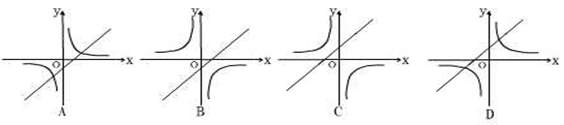
6、在同一平面直角坐标系中，函数
的图像大致是（ ）
 |
7、已知反比例函数的图象上有两点A（
，
），B（
，
），且
<0，
则
的值是（ ）
A、正数 B、负数 C、非正数 D、不能确定
8、二次函数y=x2的图象向上平移2个单位，得到新的图象函数表达式是（ ）
A、
B、
C、
D、
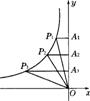9、如图，P1、P2、P3是双曲线上的三点．过这三点分别作y轴的垂线，得到三个三角形P1A10、P2A20、P3A30，设它们的面积分别是S1、S2、S3，则（
）
A、S1<S2<S3 B、S2<S1<S3 C、S1<S3<S2 D、S1=S2=S3
10、已知抛物线经过（-1,0）,（0,-3）,（2,-3）三点，则下列说法正确的是（ ）
A、该抛物线解析式为
B、对称轴为：直线
C、顶点坐标是(1,-4) D、开口向下
二. 认真填一填 (本题有6个小题, 每小题4分, 共24分)
要注意认真看清题目的条件和要填写的内容, 尽量完整地填写答案.
11、函数
的顶点坐标是
。
12、已知一个点在反比例函数
的图象上，则这个点的坐标可能为 。
13、当
时，函数
随着x的增大而增大，则m的取值范围是
。
14、若
是二次函数，则m=
。
15、已知点
（1）如果这三点都在函数
的图象上，则
的大小关系为
；
（2）如果这三点都在抛物线
上，则的大小关系为
。
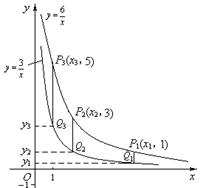16、两个反比例函数
，
在第一象限内的图象如图所示, 点P1，P2，P3，…，P2 006在反比例函数图象上，它们的横坐标分别是x1，x2，x3，…，x2 006，纵坐标分别是1，3，5，…，共2006个连续奇数，过点P1， P2，P3，…，P2 005分别作y轴的平行线，与的图象交点依次是Q1（x1，y1），Q2（x2，y2），Q3（x3，y3），…，Q2 006（x2 006，y2 006），则 y2 006=________________．
三. 全面答一答 (本题有8个小题, 共66分)
解答应写出文字说明, 证明过程或推演步骤. 如果觉得有的题目有点困难, 那么把自己能写出的解答写出一部分也可以.
17、（本小题满分6分）
已知反比例函数
的图象经过点（
），问当x等于2的时候，函数值y等于多少？
18、（本小题满分6分）
已知二次函数
当x=2时，y有最大值3，且该函数的图象经过点（1，4），求该函数解析式。
19、（本小题满分6分）
对于函数
，请回答下列问题：
（1）该函数图象可以由什么抛物线经过怎么样的平移得到？
（2）函数图象的顶点和对称轴分别是什么？
（3）当x为何值时，函数有最值，最值是多少？
20、（本小题满分8分）
已知四点Ａ(１，２），Ｂ(0，6），Ｃ(－２，20），Ｄ(－１，12）。试问：是否存在一个二次函数,使它的图象同时经过这四个点?如果存在,请求出它的解析式;如果不存在,请说明理由.
21、（本小题满分8分）
在直角坐标系中分别画出直线
和抛物线
，并说明：
（1）何时y1=y2
（2）何时y1>y2
|
| |||||||||
22、（本小题满分8分）
如图，用长为18 m的篱笆（虚线部分），两面靠墙围成矩形的苗圃.
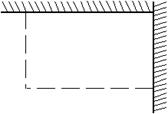（1）设矩形的一边为
（m），面积为
(m2)，求关
于的函数关系式，并写出自变量的取值范围；
（2）当为何值时，苗圃面积最大，最大面积是多少？
23、（本小题满分12分）
杭州休博会期间，嘉年华游乐场投资150万元引进一项大型游乐设施。若不计维修保养费用，预计开放后每月可创收33万元。而该游乐设施开放后，从第1个月到第x个月的维修保养费用累计为y(万元)，且y=ax2＋bx；若将创收扣除投资和维修保养费用称为游乐场的纯收益g(万元)，g也是关于x的二次函数。
（1）若维修保养费用第1个月为2万元，第2个月为4万元。求y关于x的解析式；
（2）求纯收益g关于x的解析式；
（3）问设施开放几个月后，游乐场的纯收益达到最大？几个月后，能收回投资？
24、（本小题满分12分）
先阅读下面的解题过程，然后思考后面的问题：
二次函数
①
可变形为
。
②
∴抛物线
的顶点坐标为
，即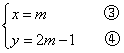
当m的值变化的时候，x，y的值也随之变化，因而y的值随x的值变化而变化。将③代入④，得
. ⑤
可见，不论m取何实数，抛物线顶点的纵坐标y和横坐标x都满足关系式⑤，因此，抛物线的顶点就始终在直线上。
（1）在上述过程中，由①到②所用的数学方法是 ，其中运用了 公式；由③④得到⑤所用的数学方法是 。
（2）根据上述接替过程提供的方法，你能确定抛物线
的顶点的纵坐标y与横坐标x之间的关系式吗？
初三数学第一学期期中学业能力测试
班级： 姓名： 得分：
一. 选择题(每小题3分, 共30分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
二. 填空题(每小题4分, 共24分)
11、 12、
13、 14、
15、
16、
三.解答题
17、（6分）
18、（6分）
19、（6分）
20、（8分）
 |
21、（8分）
|
| |||||||||
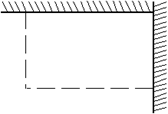22、（8分）
23、（12分）
24、（12分）