初三数学随堂练习五
1．直线L与半径为r的⊙O相交，且点O到直线L的距离为7，则r的取值范围是（ ）
A. 0 ≤ r ≤7 B . r =7 C. r ＞7 D. r≥7
2.两圆半径长分别为R和r（R＞r），圆心距为d，若关于x的方程x2－2rx＋(R－d)2=0有两相等的实数根，则两圆的位置关系是（ ）
A. 内切 B. 外切 C. 相交 D. 相切
3.一圆的外切四边形ABCD的AB=16，CD=10.则此四边形的周长为（ ）
A. 50 B. 52 C. 54 D. 56
4.⊿ABC中，AB=9，BC=5，CA=6．⊿ABC的内切圆O切AB于D，则AD的长为（ ）
A. 5 B. 10 C. 7.5 D. 4
5.相交两圆的公共弦长为6，两圆的半径分别为
，5，则这两圆的圆心距等于（ ）
A. 6 B. 2，6 C. 7 D. 1， 7
6. 半径为1和3的两圆相切，则这两圆的圆心距等于 .
7．已知⊙O1,⊙O2外切，半径分别为1cm和3cm，那么半径为5cm且与⊙O1，⊙O2都外切的圆一共可以作出_____________个。
8，△ABC的三边分别为6，8，10，则△ABC的内切圆半径为______________.
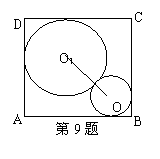9.如图，在边长为3cm的正方形ABCD中，⊙O1,⊙O2相外切，且⊙O1分别与DA，DC边相切，⊙O2分别与BA，BC边相切，则圆心距O1O2为_________________.
10．到三角形三顶点的距离都相等的点有＿＿＿＿＿＿＿个，到
三边距离都相等的点有＿＿＿＿＿＿个。
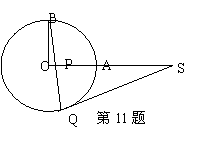
11．如图，OA、OB都是⊙O的半径，且OA⊥OB，SQ切⊙O于Q，BQ
交OA于P，求证：SP=SQ
 |
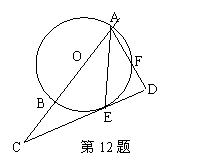12．如图，AB是⊙O的直径，AE平分∠BAF交⊙O于E，过E作
ED⊥AF于D，交AF延长线于C，试说明CD是⊙O的切线
13．如图，⊙O是△ABC的外接圆，且AB=AC=13，BC=24，PA是⊙O的切线，A为切点，割
线PD过圆心，交⊙O于另一点D，连CD，
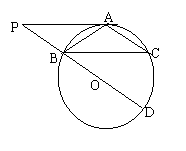（1）求证：PA∥BC； （2）求⊙O的半径及CD的长
14．如图，⊙O的直径ASB=4，∠ABC=30O，BC=
，D是线段BC的中点，
（1）试判断点D与⊙O的位置关系，并说明理由。
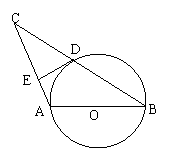（2）过D作DE⊥AC，垂足为E，求证：直线DE是⊙O的切线。
15．如图，在梯形ABCD中，AD∥BC，∠D=∠C=90O，E在CD上，AE，BE分别平分∠DAB，∠ABC，（1）以CD为直径的圆AB与直线相切吗？为什么？
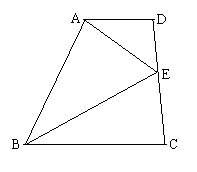（2）若以AB为直径的圆作⊙M，则⊙M与CD有何关系？证明你的结论。