九年级第二次数学月考试卷
一、选择题(本题有10小题,每小题4分,共40分,请选出各题中一个符合题意的正确选项)
1.如图1,A、B、C是圆O上三点,∠AOB=50度,则∠ACB的度数为( )
A.15度 B.25度 C.30度 D.30度
2.如图2,从A地到C地,可供选择的方案是走水路、走陆路、走空中.从A地到B地有2条水路、2条陆路,从B地到C地有3条陆路可供选择,走空中从A地不经B地直接到C地.则从A地到C地可供选择的方案有( ).
A.20种 B.8种 C. 5种 D.13种

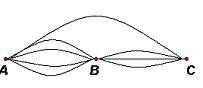

图1 图2 图3
3.如图3,一定滑轮的起重装置,滑轮半径为12cm,当重物上升4πcm时,滑轮的一条半径OA按逆时针方向旋转的度数为( )
A、12° B、30° C、60° D、90°
4.某商店举办有奖销售活动,办法如下:凡购物满100元者得奖券一张,多购多得,每10000张奖券为一个开奖单位,设特等奖1个,一等奖50个,二等奖100个,那么买100元商品的中奖概率应该是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
5.下列四个命题中正确的是( )
①与圆有公共点的直线是该圆的切线;
②垂直于圆的半径的直线是该圆的切线;
③到圆心的距离等于半径的直线是该圆的切线;
④过圆直径的端点,垂直于此直径的直线是该圆的切线
A.①② B.②③ C.③④ D.①④
6.已知正六边形的边长为12cm,则这个正六边形的边心距是( )
A.6cm
B.![]() C.6
C.6![]() D.12
D.12![]()
7.用反证法证明命题“若点P到圆心O的距离d大于圆的半径,则点P在⊙O的外部”,首先应假设( )
A. d<r B.d≤r C.点P在⊙O外 D.点P在⊙O上或⊙O内
8、 已知大⊙O1和小⊙O2内切, 它们的半径分别为3和1, 过O1作⊙O2的切线, 切点为A,则O1A的长为( )
A.![]() B.4
C.2
D.
B.4
C.2
D.![]()
9、已知圆锥的侧面展开图的面积为15πcm2 ,母线长为5cm ,则圆锥的底面半径为( )
A.![]() B.3 cm C. 4 cm D. 6 cm
B.3 cm C. 4 cm D. 6 cm
 10.下图4的转盘被划分成六个相同大小的扇形,并分别标上1, 2,3,4,5,6这六个数字,指针停在每个扇形的可能性相等。四位同学各自发表了下述见解:
10.下图4的转盘被划分成六个相同大小的扇形,并分别标上1, 2,3,4,5,6这六个数字,指针停在每个扇形的可能性相等。四位同学各自发表了下述见解:
甲:如果指针前三次都停在了3号扇形,下次就一定不会停 在3号扇形;乙:只要指针连续转六次,一定会有一次停在6号扇形;丙:指针停在奇数号扇形的概率与停在偶数号扇形的概率相等;丁:只要在转动前默默想好让指针停在6号扇形,指针停在6号扇形的可能性就会加大。
其中,你认为正确的见解有( )
A.1个 B.2个 C.3个 D.4个 图4
二、填空题(本题有6小题,每小题5分,共30分)
11.为改善市区人民生活环境,市建设污水管网工程,某圆柱型水管的直径为100 cm,截面如图5,若管内污水的面宽AB=60 cm,则污水的最大深度为_____ cm.
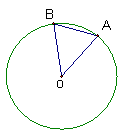
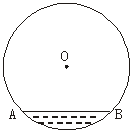
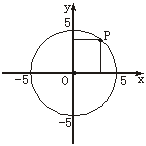
图5 图6 图7
12.如图6,弧AB所对的圆心角为40度,则弦AB所对的圆周角为_____.
 13.如图7,P(x,y)是以坐标原点为圆心,5为半径的圆周上的点,若x、y都是整数,猜想这样的P点一共有_______.
13.如图7,P(x,y)是以坐标原点为圆心,5为半径的圆周上的点,若x、y都是整数,猜想这样的P点一共有_______.
14、直角三角形的两条直角边长分别为15 cm和20 cm,则该三角形的
内切圆的周长为_____ cm..
15、如图8,是一个木制圆盘,图中两同心圆,其中大圆直径
为20cm,小圆的直径为10cm, 一只小鸟自由自在地在空中飞行,
小鸟停在小圆内(阴影部分)的概率是 。 图8
16.如图9,四边形ABCD为正方形,曲线DEFGHI,J...叫做“正方形的渐开线”,其中DE,EF,FG,GH,HI,IJ...的圆心依次按A、B、C、D......循环,当渐开线延伸开时,形成了扇形S1、S2、S3、S4和一系列的扇环S5、S6......,当AB=1时,它们的面积S1=![]() ,S2=
,S2= ![]() ,S3=
,S3= ![]() ,S4=4
,S4=4![]() ,
,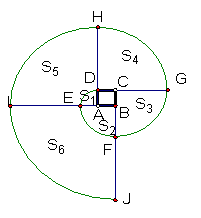 S5=6
S5=6![]() ,...那么扇环的面积S8=____
.
,...那么扇环的面积S8=____
.
三、解答题(本题有8小题,第17—20题每题8分,第21题10分,第22、23题每题12分,第24题14分,共80分)
17.将下面事件的字母写在最能代表它的概率的点上.
A:投掷一枚硬币时,得到一个正面;
B:在一小时内,你步行可以走80千米;
C:给你一个骰子中,你掷出一个3; D:明天太阳会升起来.
![]()
18.如图11,为美化校园,学校准备在一块圆形的空地上建花坛,现征集设计方案。设计要求是把圆的面积4等分,且使整个图形成对称图形(在所给的图形中画出你的设计方案,画图工具不限,画出一种方法得3分,最多得8分)。
图11
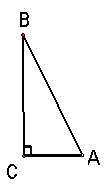 19.已知△ABC,AC=3,BC=4,∠C=90°,以点C为圆心作⊙C,半径为r.
19.已知△ABC,AC=3,BC=4,∠C=90°,以点C为圆心作⊙C,半径为r.
(1)当r取什么值时,点A、B在⊙C外;
(2)当r在什么范围时,⊙C与线段AB有且只有一个公共点。
20、如图,已知弦AB与半径相等,连结OB,并延长使BC=OB.
(1)问AC与⊙O有什么关系.
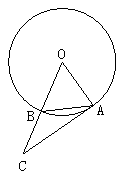 (2)请你在⊙O上找出一点D,使AD=AC(自己完成作图,并证明你的结论).
(2)请你在⊙O上找出一点D,使AD=AC(自己完成作图,并证明你的结论).
21.如图,小明、小华用4张扑克牌(方块2、黑桃4、黑桃5、梅花5)玩游戏,他俩将扑克牌洗匀后,背面朝上放置在桌面上,小明先抽,小华后抽,抽出的牌不放回。
(1)若小明恰好抽到了黑桃4。
①请在下边框中绘制这种情况的树状图;②求小华抽出的牌面数字比4大的概率。
(2)小明、小华约定:若小明抽到的牌面数字比小华的大,则小明胜;反之,则小明负。你认为这个游戏是否公平?说明你的理由。

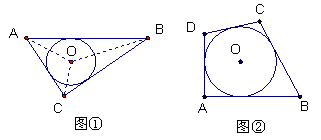
22. 阅读材料:如图①,△ABC的周长为![]() ,内切圆O的半径为r,连结OA、OB、OC,△ABC被划分为三个小三角形,用
,内切圆O的半径为r,连结OA、OB、OC,△ABC被划分为三个小三角形,用![]() 表示△ABC的面积。
表示△ABC的面积。
∵ ![]()
又∵![]() ,
, ![]() ,
, ![]()
∴![]()
![]() +
+![]() +
+![]() =
=![]() (可作为三角形内切圆半径公式)
(可作为三角形内切圆半径公式)
(1)理解与应用:利用公式计算边长分为5、12、13的三角形内切圆半径;
(2)类比与推理:若四边形ABCD存在内切圆(与各边都相切的圆,如图②),且面积为S,各边长分别为a、b、c、d,试推导四边形的内切圆半径公式;
 (3)拓展与延伸:若一个n边形(n为不小于3的整数)存在内切圆,且面积为S,各边长分别为
(3)拓展与延伸:若一个n边形(n为不小于3的整数)存在内切圆,且面积为S,各边长分别为![]() 、
、![]() 、
、![]() 、… 、
、… 、![]() ,合理猜想其内切圆半径公式(不需说明理由).
,合理猜想其内切圆半径公式(不需说明理由).
23.某电脑公司现有A,B,C三种型号的甲品牌电脑和D,E两种型号的乙品牌电脑.希望中学要从甲、乙两种品牌电脑中各选购一种型号的电脑.
(1) 写出所有选购方案(利用树状图或列表方法表示);
(2) 如果(1)中各种选购方案被选中的可能性相同,那么A型号电脑被选中的概率是多少?
 (3) 现知希望中学购买甲、乙两种品牌电脑共36台(价格如图所示),恰好用了10万元人民币,其中甲品牌电脑为A型号电脑,求购买的A型号电脑有几台.
(3) 现知希望中学购买甲、乙两种品牌电脑共36台(价格如图所示),恰好用了10万元人民币,其中甲品牌电脑为A型号电脑,求购买的A型号电脑有几台.
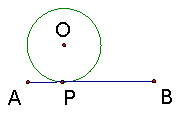 24. 如图,已知⊙O的半径为1,线段AB=4,⊙O从A端开始沿着线段AB滚向B端,设⊙O与AB的接触点是P,当P与A、B不重合时,分别过A、B两点作与⊙O相切(切点为E、F),但不与AB重合的两条射线,问:
24. 如图,已知⊙O的半径为1,线段AB=4,⊙O从A端开始沿着线段AB滚向B端,设⊙O与AB的接触点是P,当P与A、B不重合时,分别过A、B两点作与⊙O相切(切点为E、F),但不与AB重合的两条射线,问:
(1)当∠EAB=900时,AP有多长?
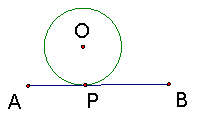
(2)当AE与BF相交于C时,且∠ACB=600,△ABC的周长是多少?
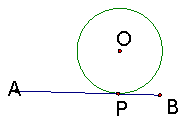
(3)当AE//BF时,点P离A端有多远?