九年级数学 第一学期期中考试
第一学期期中考试
试卷
(考试时间:90分钟,满分100分) 成绩:
一、选择题(本大题共10小题,每小题3分,共30分)每小题给出4个答案,其中只有一个是正确的,请把你选择的答案填入下表.
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
1、一元二次方程![]() 的二次项系数、一次项系数和常数项分别是(
)
的二次项系数、一次项系数和常数项分别是(
)
A. 3 ,
5 , 1
B. 3 ,
![]() , 1
, 1
C. ![]() , 5 ,
1
D.
, 5 ,
1
D. ![]() ,
, ![]() ,
, ![]()
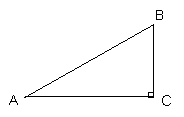 2、在
2、在![]() 中,
中,![]() ,那么
,那么![]() 是
是![]() 的( )
的( )
A.正弦 B.余弦 C.正切 D. 余 切
3、下列方程中,关于x的一元二次方程是( )
A . ![]() B.
B. ![]()
C.
![]() D.
D. ![]()
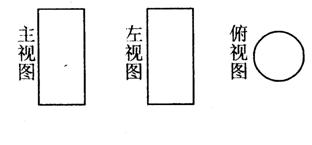
4、某物体的三视图是如图所示的3个图形,那么该物体的形状是( )
A.长方体 B.圆锥体 C.立方体 D.圆柱体
|
5、中央电视台的“幸运5 2”栏目中的“百宝箱”互动环节是一种竞猜游戏,游戏规则如下:在20个商标牌中,有5个商标牌的背面注明一定的奖金额,其余商标牌的背面是一张哭脸,若翻到哭脸,就不得奖.参与这个游戏的观众有3次翻牌的机会(翻过的牌不能再翻).某观众前两次翻牌均获得若干奖金,那么他第三次翻牌获奖的概率是( )
![]()
6、菱湖是全国著名的淡水鱼产地,某养鱼专业户为了估计他承包的鱼塘里有多少条鱼?假设这个塘里养的是同一种鱼X先捕上100条做上标记,然后放回塘里,过了一段时间,待带标记的鱼完全和塘里的鱼混合后,再捕上100条,发现其中带标记的鱼有10条,塘里大约有鱼( )
A.1600条 B.1000条 C.800条 D.600条
7、若M(-,y1),N(-,y2),P(,y3)三点都在函数![]() 中的图象上,则y1,y2,y3,的大小关系为( )
中的图象上,则y1,y2,y3,的大小关系为( )
A.y2 >y3>y1 B、y2>y1>y3
C.y3 >y1>y2 D、y3>y2>y1
8、在同一时刻的阳光下,小明的影子比小强的影子长,那么在同一路灯下( )
A.小明的影子比小强的影子长 B.小明的影子比小强的影子短
C.小明的影子和小强的影子一样长 D.无法判断谁的影子长
9、若![]() ( )
( )
A.![]() B.
B.
![]() C.
C.
![]() D.
D. ![]()
|
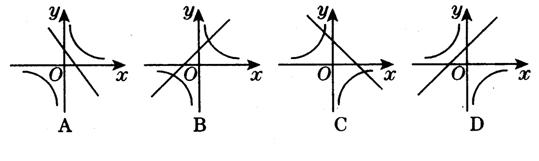
10、函数y= 与y=kx+k在同一坐标系的图象大致是图中的( )
二、填空题(本大题共5小题,每小题3分,共15分) 。请把你的答案填入下表。
| 题号 | 11 | 12 | 13 | 14 | 15 |
| 答案 |
|
|
|
|
|
11、某商场在“五一”期间推出购物摸奖活动,摸奖箱内有除颜色以外完全相同的红色、白色乒乓球各两个.顾客摸奖时,一次摸出两个球,如果两个球的颜色相同就得奖,颜色不同则不得奖.那么顾客摸奖一次,得奖的概率是 ;
12、某工厂调整内部管理机制,计划两年后使成本降低![]() %,以适应市场需求,若每年降低成本的百分数相同,设每年降低百分数为
%,以适应市场需求,若每年降低成本的百分数相同,设每年降低百分数为![]() ,则有方程:
_;
,则有方程:
_;
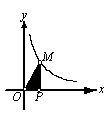 13、反比例函数
13、反比例函数![]() 在第一象限内的图像如图,点M是图像上一点,MP垂直
在第一象限内的图像如图,点M是图像上一点,MP垂直![]() 轴于点P,如果△MOP的面积为1,那么k的值是
;
轴于点P,如果△MOP的面积为1,那么k的值是
;
14、在![]() 中,
中,![]() ,
,![]() ,
,![]() ,则
,则![]() 。
。
|
 三、解答题(本大题有7题,共55分)
三、解答题(本大题有7题,共55分)
16、解下列方程组(每小题5分,共10分)
(1)![]() (5分)
(5分)
(2)![]() (5分)
(5分)
17、计算: cos245o+tan60ocos30o-3tan230o+4sin230o (6分)
|
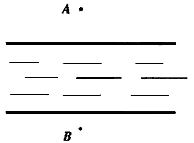
 18、如图是一条河,点A为对岸一棵大树,点B是该岸一根标杆,且AB与河岸大致垂直,现有如下器材:一个卷尺,若干根标杆,根据所学的数学知识,设计出一个测量A、B两点间距离的方案,在图上画出图形,写出测量方法。 (6分)
18、如图是一条河,点A为对岸一棵大树,点B是该岸一根标杆,且AB与河岸大致垂直,现有如下器材:一个卷尺,若干根标杆,根据所学的数学知识,设计出一个测量A、B两点间距离的方案,在图上画出图形,写出测量方法。 (6分)
 |
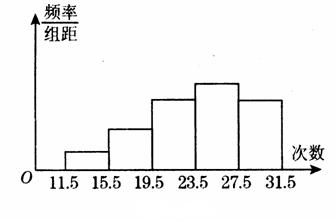
19、如图 2-l-20是某校初三年级部分学生做引体向上的成绩,进行整理后,分成五组画出的频率分布直方图,已知从左到右前四个小组的频率分别是0.05,0.15,0.25,0.30,第五小组的频数是25,根据已知条件回答下列问题:(7分)
⑴ 第五小组的频率是多少?
⑵ 参加本次测试的学生总数是多少?
⑶ 如果做 20次以上为及格(包括20次),求此次测试及格的人数是多少?
|
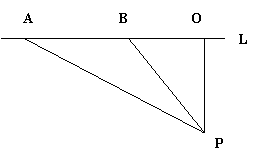
![]() 20、如图,已知测速站P到公路L的距离PO为40米,一辆汽车在公路L上行驶,测得此车从点A行驶到点B所用的时间为2秒,并测得∠APO=600,∠BPO=300,计算此车从A到B的平均速度为每秒多少米(结果保留四个有效数字),并判断此车是否超过了每秒22米的限制速度。
(8分)
20、如图,已知测速站P到公路L的距离PO为40米,一辆汽车在公路L上行驶,测得此车从点A行驶到点B所用的时间为2秒,并测得∠APO=600,∠BPO=300,计算此车从A到B的平均速度为每秒多少米(结果保留四个有效数字),并判断此车是否超过了每秒22米的限制速度。
(8分)
 |
|
21、某水果批发商场经销一种高档水果 如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克,现该商场要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元?(7分)
|
 22、若反比例函数
22、若反比例函数![]() 与一次函数
与一次函数![]() 的图象都经过点A(
的图象都经过点A(![]() ,2)(11分)
,2)(11分)
(1)求点A的坐标;(3分)
(2)求一次函数![]() 的解析式;(4分)
的解析式;(4分)
(3)设O为坐标原点,若两个函数图像的另一个交点为B,求△AOB的面积。(4分)
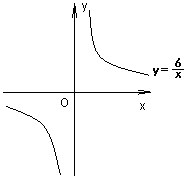
|