九年级数学期末综合测试
班级_________ 座号________ 姓名___________ 成绩___________
一、填空题。（每题3分，共36分）
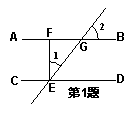1.
如右图，AB∥CD，EF⊥AB于F，若∠1=40°，则∠2的
度数为____________；
2. 一个多边形所有的外角都是相邻内角的2倍，则其边数
为____________；
3. 一条抛物线经过原点，请写出它的一个函数解析式_______________________；
4. 抛物线y=ax2 + bx +c与x轴交点为（-1，0）、（3，0），其形状与y=-2x2 相同且开口方向相同，则该抛物线的解析式为____________________________________；
5. 已知等腰梯形的腰长和中位线长都为5cm，则其周长为____________________；
| 重量（单位：kg） | 2 | 2.2 | 2.5 | 2.8 | 3 |
| 数量（单位：只） | 1 | 2 | 4 | 2 | 1 |
6. 养鸡专业户王大伯2006年养了2000只鸡，上市前，他随机抽取了10只鸡，称得重量统计如右表
根据表中数据可估计这批鸡的总重量为__________________________kg；
7. 将抛物线y=(x-1)2 +1向右平移1个单位，再向下平移2个单位，所得抛物线解析式为__________________________________；
8. 将抛物线y=2x2 绕其顶点旋转180°，得到的新图象的解析式为：__________________；
9. 开口向下的抛物线y=(m2-1)x2 +2mx+1的对称轴经过点（-1，3），则m=_____________；
10. 某校英语测评成绩由三部分组成：听力测试占成绩的20%，书面表达占成绩的30%，笔试占成绩的50%，小明上述三项成绩依次是92分、80分、84分，则小明此次英语测评成绩为_______________；
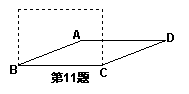11. 如图，若将四根木条钉成的矩形木框变形为平行四边
形ABCD的形状，并使其面积为矩形面积的一半，则这
个平行四边形的一个最小内角∠ABC的度数为________；
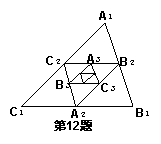12.
已知△A1B1C1的周长为1，它的三条中位线组成△A2B2C2 ，
△A2B2C2的中位线又组成△A3B3C3 ，依次类推，第2007个
三角形的周长为__________.
二、选择题。（每题4分，共24分）
13. 下列任务中，你认为哪一项采用普查更合适………………………………（ ）
A. 了解你们班同学周末时间是如何安排的 B. 了解一批圆珠笔笔心的使用寿命
C. 了解我国九年级学生的视力情况 D. 了解一批炸弹的杀伤半径
14. 若y=(x-2)2 的顶点坐标为……………………………………………… （ ）
A.（0，2） B. （0，-2） C.（2，0） D.（-2，0）
15. 一个等腰三角形的周长为20，两条边的比为1：2，那么其底边长为………（ ）
A. 10 B. 4 C. 4或10 D. 5或8
16. 如果顺次连结四边形各中点组成的四边形是菱形，那么原来的四边形的对角线（ ）
A. 互相平分 B. 相等 C.互相垂直 D. 互相垂直平分
17. 为了了解一批洗衣机的质量，从中抽取100台进行测验，这个问题中样本是…（ ）
A. 这批洗衣机的质量 B. 抽取的100台洗衣机
C. 100 D. 抽取的100台洗衣机的质量
18. 若直线y=3x+m经过一、三、四象限，则抛物线y=(x-m)2 +1的顶点在…………（ ）
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
三、解答下列各题。（共90分）
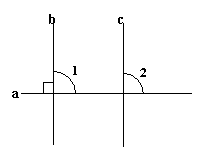
19.（8分）如图，b∥c，且b⊥a，求证：c⊥a
20.（8分）已知抛物线y = x2 + x-4
⑴用配方法求它的顶点坐标和对称轴；⑵若该抛物线与x轴的两个交点为A、B，求线段AB的长。
21．（8分）如图，矩形ABCD中，AC与BD交于点O点，BE⊥AC于E，CF⊥BD于D。
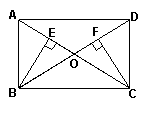求证：BE=CF
22.（8分）已知抛物线y=x2 + bx+c的顶点坐标为（1，-4），求这条抛物线的函数解析式。
23.（8分）为了预防近视，班主任老师打算了解本班同学近视的情况及引起近视的原因。
⑴你认为应该采用普查还是抽样调查，为什么？
⑵调查问题设计的合理性是很重要的，请写出两个调查中设计的问题。
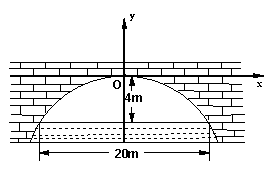24.（8分）如图是一座抛物线形拱桥，正常水位时桥下水面宽度为20m，拱顶距离水面4m，在图中直角坐标系中求该抛物线的解析式。
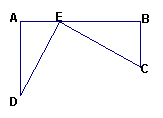
25.（8分）如图，铁路上A、B两站（视为直线上两点）相距25km，C、D为两个村庄（视为两个点），DA⊥AB于A，CB⊥AB于B，已知DA=15km，CB=10km，现要在铁路AB上建设一个土特产品收购站E，使C、D两村到E站的距离相等，则E站应建在距A站多远处，请说明理由。
26.（8分）某校餐厅计划购买12张餐桌和一批餐椅，现从甲、乙两商场了解到：同一型号的餐桌报价每张均为200元，餐椅报价每把均为50元，甲商场称：每购买一张餐桌赠送一把餐椅；乙商场规定：所有餐桌椅均按报价的八五折销售，那么，什么情况下到甲商场购买优惠？
27.（13分）某公司生产的A种产品它的成本是2元，售价3元，年销售量是100万件（即10个十万件），为了获得更好的效益，公司准备拿出一定的资金作广告。根据经验，每年投入的广告费是x（十万元）时，产品的年销售量将是原销售量的y倍，且
y =- x2 + x +1 ，如果把利润看成是销售总额减去成本费和广告费。
⑴试写出年利润S（十万元）与广告费x（十万元）的函数关系；
⑵如果投入广告费10～30万元，广告费在什么范围内，公司获得的年利润随广告费的增大而增大？；
⑶在⑴中，投入的广告费为多少万元时，公司获得的利润最大？是多少？。
28.（13分）如图，在四边形ABCD中，∠A=90°，∠ABC与∠ADC互补 。
⑴求∠C的度数；
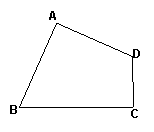⑵若BC＞CD，且AB=AD，请在图上画出一条线段，把四边形ABCD分成两部分，使得这两部分能够重新拼成一个正方形，并说明理由；
⑶若CD=6，BC=8，求AB的长。