九年级数学
上学期末教学水平检测
试卷
（考试时间120分钟，满分120分）
| 题号 | 一 | 二 | 三 | 总分 |
| 得分 | 评卷人 |
|
|
|
一、选择题（每小题 3分，共 30分）
１、某物体的三视图是如图（1）所示的三个图形，那么该物体形状是（ ）
A． 
长方体
B． 圆锥体
C． 立方体
D． 圆柱体
|
２、下列物品：①探照灯；②车灯；③太阳；④月亮；⑤台灯，所成的投影是中心投影的是（ ）
Ａ、①② Ｂ、①③ Ｃ、①②③ Ｄ、①②⑤
３、用配方法解一元二次方程
，则方程可变形为（ ）
Ａ、
Ｂ、
Ｃ、
Ｄ、
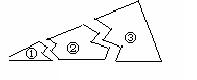
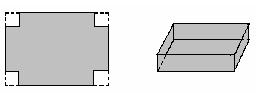
４、如图（２）,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块完全一样形状的玻璃.那么最省事的办法是带________去配. ( ).
A.① B.② C.③ D.①和②
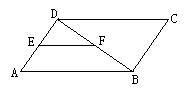
５、如图（３），在
ABCD中，EF∥AB，点F为BD的中点，EF＝４，则CD的长为（ ）
Ａ、
Ｂ、８ Ｃ、10 Ｄ、16
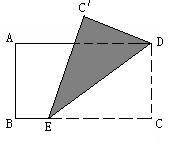
６、将一张矩形纸片ABCD如图（４）那样折叠，使顶点Ｃ落在
处，其中AB=４，若∠
,则折叠部分（阴影）面积为（ ）
Ａ、４ Ｂ、
Ｃ、８ Ｄ、
图（２） 图（３） 图（４）
７、反比例函数
的图象经过（２，５），若点（１，n）在反比例函数的图象上，则n等于（ ）
Ａ、10 Ｂ、５ Ｃ、２ Ｄ、
８、在反比例函数
的图象上有两点Ａ
，Ｂ
，且
，则
的值为（ ）
Ａ、正数 Ｂ、负数 Ｃ、非正数 Ｄ、非负数
９、由李咏主持的“幸运 52”栏目中的“百宝箱”互动环节，是一种竞猜游戏，游戏规则如下：在20个商标牌中，有5个商标牌的背面注明一定的奖金额，其余商标牌的背面是一张哭脸，若翻到哭脸，就不得奖，参与这个游戏的观众有三次翻牌机会（翻过的牌不能再翻）.某观众前两次翻牌均获得若干奖金，那么他第三次翻牌获奖的概率是（ ）
A 、
B 、
C、 
D、 
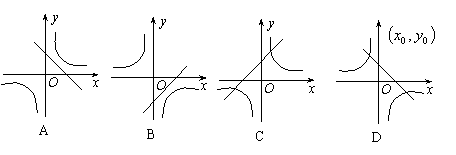10、在同一直角坐标系中，函数y=kx-k与
(k≠0)的图象大致是（ ）
| 得分 | 评卷人 |
|
|
|
二、填空题（每空2分，共 20分）
11、为了解全国中学生的睡眠状况，应采用 (“抽样调查”或“普查”)；对载人航天器“神州六号”零部件的检查，应采用 (“抽样调查”或“普查”)；
12、一元二次方程
的根是
；
13、已知等腰三角形的一边等于5,另一边等于6,则它的周长等于____ ___；
14、一种收音机刻度盘的波长
和频率
分别是用米（m）和千赫兹（kHz）为单位标刻的。波长和频率满足关系式
，这说明波长越大，频率就越 ；
15、老师给出一个函数，甲、乙、丙各正确指出了这个函数的一个性质：
甲：函数的图象经过第一象限； 乙：函数的图象经过第三象限；
丙：在每个象限内，y随x的增大而减小．
请你根据他们的叙述构造满足上述性质的一个函数： ．
16、2008年北京奥运会吉祥物“福娃”于2005年11月11日向全世界发布，分别是“贝贝、京京、欢欢、迎迎、妮妮”
图（５）。现用①－⑤号小球分别表示五个“福娃”，将小球放入一个不透明的盒子里，从盒子里任意拿出一个，再放回；摇匀后又重新拿一次，两次都拿到④号“福娃迎迎”的概率为
；
|
；
18、国家对药品实施价格调整，某药品经过两次降价后，每盒的价格由原来的60元降至48.6元，那么平均每次降价的百分率是 ；
19、某闭合电路中，电源的电压为定值，电流Ｉ（Ａ）与电阻Ｒ（Ω）成反比例，图（６）表示的是该电路中电流Ｉ与电阻Ｒ之间关系的图象，则用电阻Ｒ表示电流Ｉ的函数解析式为
。
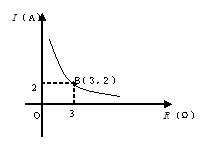图（６）
| 得分 | 评卷人 |
|
|
|
三、解答题（共70分）
20、（每题5分，共10分）
①用配方法解方程 
②解方程 
21、（８分）如图，在△ABC中，AB=BC，Ｄ、Ｅ、Ｆ分别是BC、AC、AB边上的中点， （１）求证：四边形BDEF是菱形；（６分）
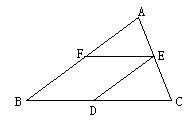（２）若AB=12 cm，求菱形BDEF的周长。（２分）
22、本题有Ａ、Ｂ两类题，Ａ类题满分7分，Ｂ类题满分10分。请你选择其中一类证明。
（Ａ类）如图(７)，DE⊥AB，DF⊥AC，垂足分别为Ｅ、Ｆ，请你从下面三个条件中，再选出两个作为已知条件，另一个为结论，推出一个正确的命题（只需写出一种情况），
① AB = AC ； ② BD = CD ； ③BE = CF
已知DE⊥AB，DF⊥AC，垂足分别为Ｅ、Ｆ， ＝ ， ＝ 。
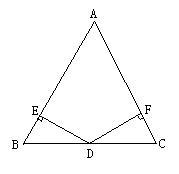求证： ＝ 。
证明：
图（７）
（Ｂ类）如图（８），EG ∥AF ，请你从下面三个条件中，再选出两个作为已知条件，另一个为结论，推出一个正确的命题（只需写出一种情况），
①AB =AC ； ②DE =DF ； ③BE =CF
已知：EG∥AF ， ＝ ， ＝ 。
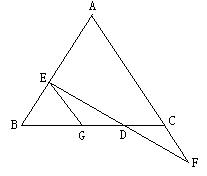求证： ＝ 。
证明：
图（８）
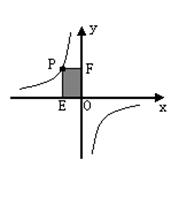
23、（9分）已知，如图在反比例函数图象上有一点Ｐ
，过Ｐ点作PE⊥
轴，PF⊥
轴，PE、PF 与轴、 轴所围成的矩形面积为５，试确定该反比例函数的解析式。
|
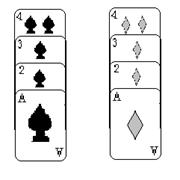
24、（９分）如图是从一副扑克牌中取出的两组牌，分别是黑桃１、２、３、４和方块１、２、３、４，将它们背面朝上分别重新洗牌后，从两组牌中各摸出一张，那么摸出的两张牌的牌面数字之和等于5的概率是多少？请你用列举法（列表或画树状图）加以分析说明。
25、（12分）如图，AB表示路灯，CD、
表示小明所在两个不同位置：
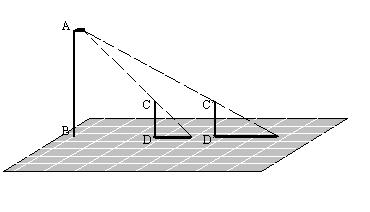
（1）在图中分别画出这两个不同位置小明的影子（保留作图痕迹）；(4分)
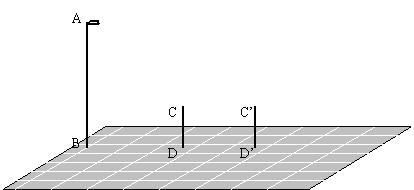（2）小明发现在的位置上，他的影子长是自己身高的2倍，他又量得自己的身高为1.6米，此时他离路灯的距离为6.8米，你能帮他算出路灯的高度吗？（８分）
26、（12分）李大伯从市场上买回一块矩形铁皮，他将此矩形铁皮的四个角各剪去一个边长为１米的正方形后，剩下的部分刚好能围成一个容积为15米
的无盖长方体运输箱（如图）。且此长方体运输箱底面的长比宽多２米，现已知购买这种铁皮每平方米需20元，问李大伯购买这张铁皮共花了多少元钱？
参考答案：
一、选择题：（每小题 3分，共 30分）
１、Ｄ； ２、Ｄ； ３、Ｂ； ４、Ｃ； ５、Ｂ； ６、Ｄ； ７、Ａ； ８、Ａ； ９、Ｃ； 10、Ｄ
二、填空题（每空2分，共 20分）
11、抽样调查；普查； 12、
，
； 13、16或17； 14、小
15、答案不唯一（反比例函数，k>0）如：
； 16、
； 17、120 18、
%；
19、
三、解答题（共70分）
20、（每小题5分，共10分）
① 解：移项，得
……………………1分
配方，得
……………2分
…………………4分
解这个方程，得
即
，
………………5分
（若用其它方法解对，得1分）
② 解：原式变形为
……………………1分
……………………2分
则 
……………4分
即
，
………………5分
(若用其它方法解,参照给分)
21、（共８分，第1小题6分，第2小题2分）
（1）证明：
D、E、F分别是BC、AC、AB边上的中点，
DE∥AB；EF∥BC
四边形BDEF是平行四边形
……………4分
又 
；
，且AB = BC，
DE = EF
四边形BDEF是菱形。
………………6分
另解：证明：D、E、F分别是BC、AC、AB边上的中点，
；， ………………2分
又 AB = BC
BD=BF=
DE=EF=BF=BD
四边形BDEF是菱形。
………………6分
（2）AB=12 cm，F为AB的中点
BF=6 cm
………………1分
菱形BDEF的周长为：
………………2分
22、（A类，７分）
已知：………AB = AC ； BD = CD ；
求证：BE = CF …………………………………1分
证明： AB = AC
∠B=∠C
DE⊥AB，DF⊥AC
∠BED=∠CFD=90O …………………………………3分
在△BDE和△CDF中
∠B=∠C
∠BED=∠CFD=90O ……………………………5分
BD=CD
△BDE
△CDF（AAS） ……………………………6分
BE = CF
……………………………7分
（B类，10分）
已知：………AB =AC ；DE =DF ；
求证：BE =CF …………………………………1分
证明： EG∥AF
∠GED=∠F
…………………………………2分
∠BGE=∠BCA …………………………………3分
AB =AC
∠B=∠BCA
…………………………………4分
∠B=∠BGE
BE=EG
…………………………………5分
在△DEG和△DFC中，
∠GED=∠F
DE =DF …………………………7分
∠EDG=∠FDC
△DEG△DFC（ASA） …………………………………8分
EG=CF
…………………………………9分
BE=CF
…………………………………10分
（注：A、B两类题的另两种情况的证明参照以上评分标准）
23、（9分）
解：设该反比例函数解析式为
，点P的坐标为 ……………1分
P点在的图象上
…………………………………3分
又矩形PEOF的面积=PF
PE=5
…………………………………4分
而PF=
，PE=
，=5 …………………………………6分
P点在第二象限，
…………………………………8分
即
，也就是反比例函数解析式为
…………………………9分
24、（9分）
可以用下表列举所有可能得到的牌面数字之和：
|
黑桃 | 1 | 2 | 3 | 4 |
| 1 | 1+1=2 | 2+1=3 | 3+1=4 | 4+1=5 |
| 2 | 1+2=3 | 2+2=4 | 3+2=5 | 4+2=6 |
| 3 | 1+3=4 | 2+3=5 | 3+3=6 | 4+3=7 |
| 4 | 1+4=5 | 2+4=6 | 3+4=7 | 4+4=8 |
………………………6分
从上表可知，共有16种情况，每种情况发生的可能性相同，而两张牌的牌面数字之和等于5的情况共出现4次，因此牌面数字之和等于5的概率为：
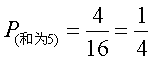…………………9分
（注：列树状图分析的评分标准同上）
25、（12分）
（１）（４分）
（２）（８分）解：在位置上影长为：
…………………2分
………………………7分
AB = 5
即：路灯的高度为5米。 ………………………8分
26、（12分）
解：设这种运输箱底部宽为
米，则长为
米， ………………………１分
依题意，有
………………………５分
化简，得
………………………７分
这种运输箱底部长为5米，宽为3米。 ………………………８分
由长方体展开图知，要购买的矩形铁皮面积为：
………10分
做一个这样的运输箱要花
元钱。
………………………12分