九年级数学下二次函数测试题
姓名 学号 得分
A卷(100分)
一、选择题:(把正确答案的序号填在下表中,每题3分,共36分)
1、抛物线![]() 的顶点坐标是( )
的顶点坐标是( )
 (A) (-2,3) (B)(2,3) (C)(-2,-3) (D)(2,-3)
(A) (-2,3) (B)(2,3) (C)(-2,-3) (D)(2,-3)
2、抛物线![]() 与
与![]() 的形状相同,而开口方向相反,则
的形状相同,而开口方向相反,则![]() =( )
=( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
3.与抛物线![]() 的形状大小开口方向相同,只有位置不同的抛物线是( )
的形状大小开口方向相同,只有位置不同的抛物线是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.二次函数![]() 的图象上有两点(3,-8)和(-5,-8),则此拋物线的对称轴是( )
的图象上有两点(3,-8)和(-5,-8),则此拋物线的对称轴是( )
A.![]() =4 B.
=4 B. ![]() =3 C.
=3 C. ![]() =-5 D.
=-5 D. ![]() =-1。
=-1。
5.抛物线![]() 的图象过原点,则
的图象过原点,则![]() 为( )
为( )
A.0 B.1 C.-1 D.±1
6.把二次函数![]() 配方成顶点式为( )
配方成顶点式为( )
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
7.二次函数![]() 的图象如图所示,则
的图象如图所示,则![]() ,
,![]() ,
,![]() ,
,![]() 这四个式子中,
这四个式子中, ![]() 值为正数的有( )A.4个 B.3个 C.2个 D.1个
值为正数的有( )A.4个 B.3个 C.2个 D.1个
 8、已知二次函数
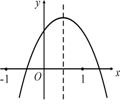
8、已知二次函数![]() 的图象如图所示,给出以下结论
的图象如图所示,给出以下结论
:① ![]() ;②
;② ![]() ;③
;③![]() ;④
;④![]() .
.
其中所有正确结论的序号是( )
A. ③④ B. ②③ C. ①④ D. ①②
9.直角坐标平面上将二次函数y=-2(x-1)2-2的图象向左平移1个单位,再向上平移1个单位,则其顶点为( )A.(0,0) B.(1,-2) C.(0,-1) D.(-2,1)
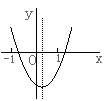 10.函数
10.函数![]() 的图象与
的图象与![]() 轴有交点,则
轴有交点,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
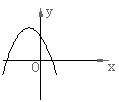
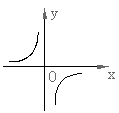 11.已知反比例函数
11.已知反比例函数![]() 的图象如右图所示,则二次函数
的图象如右图所示,则二次函数![]() 的图象大致为( )
的图象大致为( )
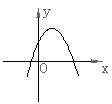
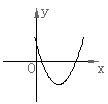
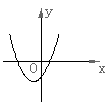
|
|
|
|
二、填空题:(每空3分,共30分)
1.已知抛物线![]() ,请回答以下问题:
,请回答以下问题:
⑴ 它的开口向 ,对称轴是直线 ,顶点坐标为 ;
⑵ 图象与![]() 轴的交点为
,与
轴的交点为
,与![]() 轴的交点为
。
轴的交点为
。
2.抛物线![]() 过第二、三、四象限,则
过第二、三、四象限,则![]() 0,
0,![]() 0,
0,![]() 0.
0.
3.抛物线![]() 可由抛物线
可由抛物线![]() 向 平移 个单位得到.
向 平移 个单位得到.
4.顶点为(-2,-5)且过点(1,-14)的抛物线的解析式为 .
5.对称轴是![]() 轴且过点A(1,3)、点B(-2,-6)的抛物线的解析式为
.
轴且过点A(1,3)、点B(-2,-6)的抛物线的解析式为
.
6.已知二次函数![]() ,则当
,则当![]() 时,其最大值为0.
时,其最大值为0.
7.二次函数![]() 的值永远为负值的条件是
的值永远为负值的条件是![]() 0,
0,![]() 0.
0.
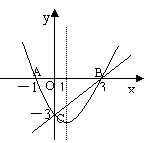 8如图,在同一直角坐标系中,二次函数的图象与两坐标轴分别交于A(-1,0)、点B(3,0)和点C(0,-3),一次函数的图象与抛物线交于B、C两点。
8如图,在同一直角坐标系中,二次函数的图象与两坐标轴分别交于A(-1,0)、点B(3,0)和点C(0,-3),一次函数的图象与抛物线交于B、C两点。
⑴二次函数的解析式为 .
⑵当自变量![]() 时,两函数的函数值都随
时,两函数的函数值都随![]() 增大而增大.
增大而增大.
⑶当自变量 时,一次函数值大于二次函数值.
⑷当自变量![]() 时,两函数的函数值的积小于0.
时,两函数的函数值的积小于0.
9.已知抛物线![]() 与
与![]() 轴的交点都在原点的右侧,则点M(
轴的交点都在原点的右侧,则点M(![]() )在第 象限.
)在第 象限.
10.已知抛物线![]() 与
与![]() 轴交于点A,与
轴交于点A,与![]() 轴的正半轴交于B、C两点,且BC=2,S△ABC=3,则
轴的正半轴交于B、C两点,且BC=2,S△ABC=3,则![]() = ,
= ,![]() = .
= .
三、解答题:(1-2每题10分,3题14分共34分)
1. 某商店经营一种水产品,成本为每千克40元的水产品,据市场分析,若按每千克50元销售,一个月能售出500千克;销售价每涨1元,月销售量就减少10千克,针对这种水产品的销售情况,请回答
下列问题(1)当销售单价为每千克55元时,计算销售量和月利润.
(2)设销售单价为每千克x元,月销售利润为y元,求y与x的函数关系式.
(3)销售单价定为多少元时,获得的利润最多?
 2、已知二次函数
2、已知二次函数![]() 的图象经过点(1,0)和(-5,0)两点,顶点纵坐标为
的图象经过点(1,0)和(-5,0)两点,顶点纵坐标为![]() ,求这个二次函数的解析式。
,求这个二次函数的解析式。
 24.已知,如图,直线
24.已知,如图,直线![]() 经过
经过![]() 和
和![]() 两点,它与抛物线
两点,它与抛物线![]() 在第一象限内相交于点P,又知
在第一象限内相交于点P,又知![]() 的面积为
的面积为![]() ,求
,求![]() 的值;
的值;
B卷(50分)
一、填空题(15分)
1、已知一列数:1,―2,3,―4,5,―6,7,… 将这列数排成下列形式:按照上述规律排下去,那么第10行从左边数第5个数等于 .
第1行 1
第2行 -2 3
第3行 -4 5 -6
第4行 7 -8 9 -10
第5行 11 -12 13 -14 15
2、将抛物线![]() 向下平移3个单位,再向左平移4个单位得到抛物线
向下平移3个单位,再向左平移4个单位得到抛物线![]() ,则原抛物线的顶点坐标是 。
,则原抛物线的顶点坐标是 。
3、函数![]() 当
当![]() 时,
时,![]() 的取值范围是
。
的取值范围是
。
二、(9分)已知抛物线![]() 与
与![]() 轴交于A、B两点,且点A在
轴交于A、B两点,且点A在![]() 轴的负半轴上,点B在
轴的负半轴上,点B在![]() 轴的正半轴上。(1)求实数
轴的正半轴上。(1)求实数![]() 的取值范围;(2)设OA、OB的长分别为
的取值范围;(2)设OA、OB的长分别为![]() 、
、![]() ,且
,且![]() ∶
∶![]() =1∶5,求抛物线的解析式。
=1∶5,求抛物线的解析式。
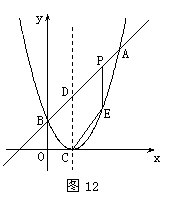
如图12,已知二次函数图象的顶点坐标为C(1,0),直线![]() 与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴
与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴![]() 上.
上.
(1)求![]() 的值及这个二次函数的关系式;
的值及这个二次函数的关系式;
(2)P为线段AB上的一个动点(点P与A、B不重合),过P作![]() 轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为
轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为![]() ,点P的横坐标为
,点P的横坐标为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)D为直线AB与这个二次函数图象对称轴的交点,在线段AB上是否存在一点P,使得四边形DCEP是平行四形?若存在,请求出此时P点的坐标;若不存在,请说明理由.
 |