九年级第四次月考数学试卷

九年级第四次月考数学试卷

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  得分：　　　

（本卷共八大题，计23小题，满分150分，考试时间120分钟。）

　 嗨！同学们好！俗话说，书山有路勤为径！同学们，在答卷前，请认真审题，只要你理解概念，仔细运算，积极思考，相信会考出理想的数学成绩！加油哦。

一、选择题（每小题4分，共40分）

1、如果（y>0）是二次根式，那么，化为最简二次根式是（　）．

　　　A．（y>0）　　 B．（y>0）　　C．（y>0）　　 D．以上都不对

2、下列图形中，是中心对称图形，但不是轴对称图形的是（　）．

　　A．正方形　　B．矩形　　C．菱形　　D．平行四边形

3、方程x（x-1）=2的两根为（　）．

　　　A．x₁=0，x₂=1　　 B．x₁=0，x₂=-1　　C．x₁=1，x₂=2　　 D．x₁= -1，x₂=2

4、一个小组若干人，新年互送贺卡，若全组共送贺卡72张，则这个小组共（　）．

　　　A．12人　　B．18人　　C．9人　　D．10人

5、从正方形铁片，截去2cm宽的一条长方形，余下的面积是48cm²，则原来的正方形铁片的面积是（　）．

　　A．8cm　　 B．64cm　　 C．8cm² 　　D．64cm²

6、如图1，A、B、C三点在⊙O上，∠AOC=100°，则∠ABC等于（　）．

A．140°　　B．110°　　C．120°　　D．130°

　　　　　　

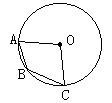
　　　 （1）　　　　　　　　　　　  （2）

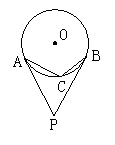
7、如图2，PA、PB分别切圆O于A、B两点，C为弧AB上一点，∠APB=30°，则∠ACB=（　）．

　　  A．60°　　B．75°　　C．105°　　D．120°

8、已知两圆的半径分别为5cm和7cm，圆心距为8cm，那么这两个圆的位置关系是（　）

　　  A．内切　　  B．相交　　C．外切　　D．外离

9、在半径为50cm的圆形铁皮上剪去一块扇形铁皮，用剩余部分制作成一个底面直径为80cm，母线长为50cm的圆锥形烟囱帽，则剪去的扇形的圆心角度数为（　）

　　　A．228°　　B．144°　　C．72°　　D．36°

10、一次抛掷三枚均匀的硬币，求下列事件的概率：正好一个正面朝上的概率是（　　）　　　　　　　　　　　　　　　　　　　　　 A、　　B、　　C、　　 D、

二、填空题（每小题5分，共30分）

11、已知等腰直角三角形的直角边的边长为，那么这个等腰直角三角形的周长是________．（结果用最简二次根式）

12、某化工厂今年一月份生产化工原料15万吨，通过优化管理，产量逐年上升，第一季度共生产化工原料60万吨，设二、三月份平均增长的百分率相同，均为x，可列出方程为_________　　　　　　　　　　　　　　　　　　　　　　　　　　　　 _．

13、一个小球由静止开始在一个斜坡上向下滚动，通过仪器观察得到小球滚动的距离s（m）与时间t（s）的数据如下：

时间t（s）	1	2	3	4	……
距离s（m）	2	8	18	32	……

　　写出用t表示s的关系式为_______．

14、边长为a的正三角形的内切圆半径是_________．

15、粮仓顶部是一个圆锥形，其底面周长为36m，母线长为8m，为防雨需在粮仓顶部铺上油毡，如果按用料的10%计接头的重合部分，那么这座粮仓实际需用________m²的油毡．

16、一个袋子里装有5个白球，3个红球，2个黑球，每个球除颜色外都相同，任意摸出一个球，是黑球的概率是______________

三、解答题： （共80分）

17、（每小题6分，满分12分）

（1）计算：（4-3）÷2

 

　　　

（2）如图，在平面直角坐标系中，A（-3，1），B（-2，3），C（0，2），画出△ABC关于x轴对称△A′B′C′，再画出△A′B′C′关于y轴对称△A″B″C″，那么△A″B″C″与△ABC有什么关系，请说明理由．

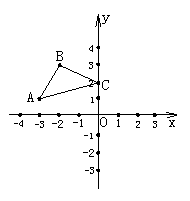
18、（本题满分8分）在一块长12m，宽8m的长方形平地中央，划出地方砌一个面积为8m²的长方形花台，要使花坛四周的宽地宽度一样，则这个宽度为多少?

19、（本题满分12分）

一个小球以10m/s的速度在平坦地面上开始滚动，并且均匀减速，滚动20m后小球停下来．

　　（1）小球滚动了多少时间?

　　（2）平均每秒小球的运动速度减少多少?

　　（3）小球滚动到5m时约用了多少时间（精确到0.1s）?

20、（本题满分8分）

如图，已知AB=AC，∠APC=60°

　　（1）求证：△ABC是等边三角形．

（2）若BC=4cm，求⊙O的面积．

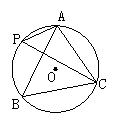
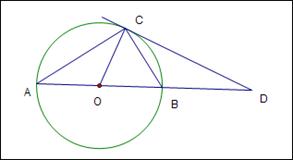
21、（本题满分10分）如图，AB为⊙O的直径，C是⊙O上一点，D在AB的延长线上，且∠DCB=∠A．

　　（1）CD与⊙O相切吗？如果相切，请你加以证明，如果不相切，请说明理由．

（2）若CD与⊙O相切，且∠D=30°，BD=10，求⊙O的半径．

　　　　　　　　　　　　　　　　　　　　　　　　　　　 

22、（本题满分10分）等边△ABC的边长为a，求其内切圆的内接正方形DEFG的面积．

23、（本题满分10分）已知扇形的圆心角为120°，面积为300cm²．

　　（1）求扇形的弧长；

　　（2）若将此扇形卷成一个圆锥，则这个圆锥的轴截面面积为多少？

24、（本题满分10分）一个袋子种装有个红球和个绿球，任意摸出一球，记录颜色放回，在任意摸出一个球，记录颜色后放回，请你求出两次都摸到红球的概率.

　

答案:

一、CDDCD　DCBCB

二、11、 ， 12、15+15(1+x)+15(1+x)²=60，13、s=2t²，14、，

15、158.4，16、，

三、17、（1）解：（4-3）÷2=4÷2-3÷2

　　=2-

（2）画图略，△A″B″C″与△ABC的关系是关于原点对称．

18、设宽为x，则12×8-8=2×8x+2（12-2x）x

　　整理，得：x²-10x+22=0

　  解得：x₁=5+（舍去），x₂=5-

19、（1）小球滚动的平均速度==5（m/s）　小球滚动的时间：=4（s）　

（2）=2.5（m/s）　

（3）小球滚动到5m时约用了xs　

　　依题意，得：x·=5，整理得：x²-8x+4=0

　　解得：x=4±2，所以x=4-2

20、（1）证明：∵∠ABC=∠APC=60°，

∠ACB=∠ABC=60°，∴△ABC为等边三角形．

（2）解：连结OC，过点O作OD⊥BC，垂足为D，

在Rt△ODC中，DC=2，∠OCD=30°，

设OD=x，则OC=2x，∴4x²-x²=4，∴OC=

21、解：（1）CD与⊙O相切

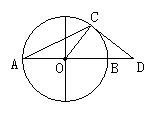　　理由：①C点在⊙O上（已知）

　　②∵AB是直径

　　∴∠ACB=90°，即∠ACO+∠OCB=90°

　　∵∠A=∠OCA且∠DCB=∠A

　　∴∠OCA=∠DCB

　　∴∠OCD=90°

　　综上：CD是⊙O的切线．

　　（2）在Rt△OCD中，∠D=30°

　　∴∠COD=60°

　　∴∠A=30°

　　∴∠BCD=30°

　　∴BC=BD=10

　　∴AB=20，∴r=10

　　答：（1）CD是⊙O的切线，（2）⊙O的半径是10．

22、设BC与⊙O切于M，连结OM、OB，

则OM⊥BC于M，连OE，作OE⊥EF于N，则OE=OM=a，∠EOM=45°，OE=a，

∵EN=a，EF=2EN=a，∴S_正方形=a²．

23、∵300=

　　∴R=30

　　∴弧长L=20（cm）

（2）如图所示：

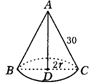　　∵20=20r

　　∴r=10，R=30

　　AD==20

　　∴S_轴截面=×BC×AD

=×2×10×20=200（cm²）

因此，扇形的弧长是20cm卷成圆锥的轴截面是200cm²．

24、两次都摸到红球的概率是.