九年级第一学期期中考试数学试卷

九年级第一学期期中考试数学试卷

（考试时间：90分钟；满分：100分；命题人：姚红阳）

说明：1．答题前，请将学校、试室、班级、姓名和座位号写在第二卷密封线内．不得在

试卷上做任何标记.

　　　　2．全卷分第一卷和第二卷，共6页．第一卷为选择题、填空题．第二卷为解答题．

第一卷选择题(1－10)，填空题(11－15)每小题的所有答案必须写在第二卷的指

定表格内．

3．本次考试不使用计算器．考试完毕，考生只需上交第二卷．

　　 　

第一卷

 

一、选择题（本大题共10小题，每小题3分，共30分）

每小题给出４个答案，其中只有一个是正确的．请把正确选项填入第二卷的

答题表一内，否则不给分．

１．方程的解是

Ａ．　 Ｂ．　　Ｃ．，　　Ｄ． ，

２．反比例函数的图象在

　　Ａ．第一、三象限　　Ｂ．第二、四象限　　Ｃ．第一、四象限　　Ｄ．第二、三象限

３．下列命题中，假命题的是

Ａ．三角形三条角平分线相交于一点　　 Ｂ．等腰梯形同一底上的两个角相等

Ｃ．对角线相等的四边形是矩形　　　　 Ｄ．等边三角形的三个内角都等于60°

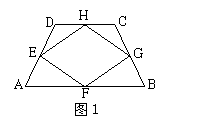
４．如图１所示，在梯形ABCD中，AB∥CD，AD=BC，点E、

F、G、H分别是梯形各边的中点，则四边形EFGH一定是

　　A．菱形　　Ｂ．矩形　　Ｃ．正方形　　Ｄ．等腰梯形

５．利用配方法解方程，配方后正确的是

Ａ．　 Ｂ． 　Ｃ．　　Ｄ．

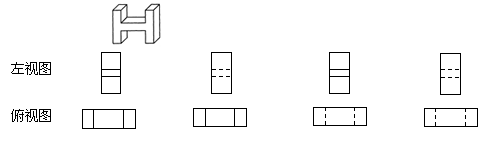６．下面是立体字母”　　　　”的两种视图，其中正确的是

Ａ　　　　　　　Ｂ　　　　　 　　Ｃ　　　　　　　Ｄ

７．下列选项中,不是反比例函数关系的是　　　

Ａ．质量一定时，密度与体积的关系　　 Ｂ．压力一定时，压强与面积的关系

Ｃ．电压一定时，电流与电阻的关系　 　Ｄ．速度一定时，路程与时间的关系

８．

如图２所示，□ABCD中，∠BCD的平分线CE交AD于

点Ｅ，DE = 2AE = 4cm，则□ABCD的周长等于

Ａ．16cm　　Ｂ．20cm　　Ｃ．24cm　　Ｄ．28cm

９．要在一块边长为10米的正方形荒地上建一个花坛, 花坛四周是宽度相等的小路，中央

是正方形的花圃，要求四周小路的总面积达到19米²．小明为求出四周小路的宽度，

列出的方程为，那么小明设的未知数表示

Ａ．小路的宽　 Ｂ．四周小路的面积　 Ｃ．中央花圃的边长　 Ｄ．中央花圃的面积

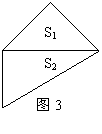10．将一副三角板如图3所示的放置，有两条边恰好完全重合，则上

下两块三角板的面积之比:

A．: 2　　　B．: 3　　　C．3 :　　　D．2 :

　　　

二、填空题(本大题共5小题，每小题3分，共15分)

请将正确答案填在第二卷的答题表二内相应的题号下，否则不给分．

11．关于的一元二次方程的两个根分别是、，那么

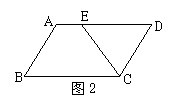
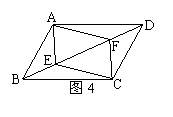
12．如图４所示，BD是□ABCD的对角线，E、F在BD上，

若不增加任何字母与辅助线，要使得四边形AECF是平行

四边形，则还需添加的一个条件是

13．反比例函数的图象有下列性质：①在每一象限内，y值随x值的增大而增大；　

②过图象上一点作x轴、y轴的平行线，与坐标轴围成的矩形面积为4；那么

14．甲公司前年缴税40万元，今年缴税48万元，设公司缴税

的年平均增长率为x，则可列方程 ．　

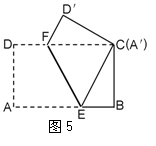
15．如图５所示，将矩形ABCD沿EF折叠，使得点Ａ恰与

点Ｃ重合．折叠后测得∠BCE = 30°，BE＝2cm，那么

折痕EF =  cm.

九年级第一学期期中考试数学试卷

题 号	一	二	三
	1～10	11～15	16	17	18	19	20	21	22
得 分

第二卷

一、选择题(每小题3分,共30分):

答题表一
题 号	1	2	3	4	5	6	7	8	9	10
答 案

二、填空题(每小题3分,共15分):

答题表二
题 号	11	12	13	14	15
答 案

三、解答题（共55分）

16．（12分）解下列方程:

(1)(6分)　　　　　　　　　  (2)(6分)

解:　　　　　　　　　　　　　　　　　　　　  解:

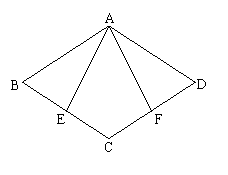17．（6分）在菱形ABCD中，点E、F分别是BC、CD的中点

求证：AE=AF

　　证明：

18．（6分）某商场经销一批毛衣，平均每天可售出20件，每件盈利50元．为了增加利润，商

家决定降价促销．经调查发现：毛衣售价每降1元，平均每天可多售出2件，若商场销售这

种毛衣要求平均每天盈利达到1600元，那么每件毛衣应降价多少元？

解：

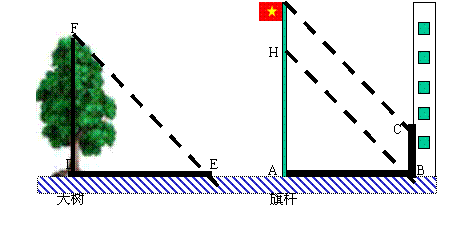
19．（７分）光明学校的旗杆附近有一棵大树，如图所示，在某一时刻旗杆在阳光下的影子有

一部分在地面上(线段AB)，另有一部分在某一建筑物上(线段BC)

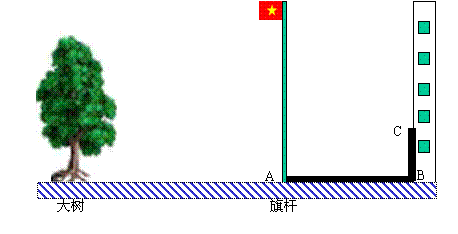
(1) (3分) 画出在同一时刻下大树的影子(用线段DE表示)

(2) (４分) 已知旗杆的高为10米．同一时刻测得旗杆的影子AB=9.6米，BC=2米，大树的影子

DE=9米，求大树的高

解：

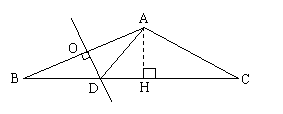
20．(７分)在△ABC中，∠B=22.5°，∠C=30°，AB的垂直平分线OD交BC边于点D，连结AD

(1)　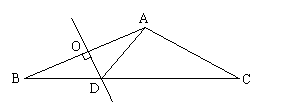  (３分)求∠DAC的度数

解：

(2) (4分)若AC=4cm，求△ABC的面积(结果保留根号)

　 解：

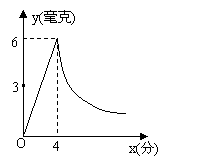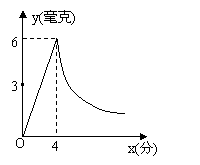
21．(7分) 某医院对病房采用药薰消毒法进行消毒，已知药

物燃烧时，病房内每立方米空气中的含药量y(毫克)与时

间x(分钟)成正比例关系；药物燃烧完后，y与x成反比例

关系(如图)．药物经4分钟燃烧完毕时测得病房内每立方米

空气中的含药量为6毫克，请根据题中所提供的信息，回答

下列问题：

(1)(4分)药物在燃烧过程中，y与x的函数关系式为：　　　　　　　 ，自变量x的取值

范围是　　　　　　　　；

　药物燃烧完毕后，y与x的函数关系式为：　　 　　　　　　　 ，自变量x的取值范围

是　　　　　　　　；

(2)(3分)研究表明，当病房内每立方米空气中的药物含量不少于3毫克并且持续时间不低于

5分钟时，才能有效杀灭病房内的病菌，那么此次消毒是否有效？为什么？

　解：

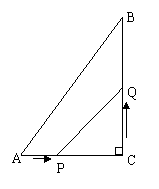
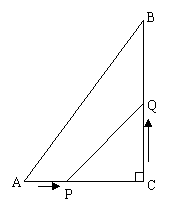22．(10分) 如图，在Rt△ABC中，∠ACB=90°，AC=10cm，BC=15cm，点P从A出发沿AC

向C点以1厘米/秒的速度匀速移动；点Q从C出发沿CB向B点以2厘米/秒的速度匀速移

动．点P、Q分别从起点同时出发，移动到某一位置时所需时间为t秒

(1)　　(2分)当t = 4时，求线段PQ的长度

解：

(2)　　(4分)当t为何值时，△PCQ的面积等于16cm²？

解：

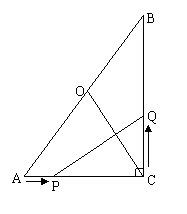(3) (4分)点O为AB的中点，连结OC，能否使得PQ⊥OC？若能，求出t的值；若不能，请说

明理由．

　解：

参 考 答 案

一、选择题(每小题3分,共30分):

答题表一
题 号	1	2	3	4	5	6	7	8	9	10
答 案	C	B	C	A	D	B	D	B	C	A

二、填空题(每小题3分,共15分):

答题表二
题 号	11	12	13	14	15
答 案	1	BE=DF或∠AED=∠CFB 或∠AFB=∠CED 或∠DAF=∠BCE……			4

（注：第12题中填写“AE=CF”或“AF=CE”不正确）

三、解答题（共55分）

16．（12分）解下列方程:

(1)(6分)　　　　　　　　　　(2)(6分)

解: 　　　　　　　　　 解:

　  　　　　　　　　

　　　　　  　 ………………2分　　　　　　　

　 …………4分　　　　　　  或　 ……4分 

所以　　 　……………6分　　　　  所以　 　　…………6分

17．（6分）在菱形ABCD中，点E、F分别是BC、CD的中点

求证：AE=AF

证明：∵　四边形ABCD是菱形

∴　∠B=∠D

　  AB=BC=CD=DA　　　　 ………2分　

∵　E、F是BC、CD的中点　

∴　BE=DF　　　　　　　　 ………4分

∴　△ABE≌△ADF　　　　 ………5分　

∴　AE=AF　　　　　　　　 ………6分　

18．（6分）某商场经销一批毛衣，平均每天可售出20件，每件盈利50元．为了增加利润，商

家决定降价促销．经调查发现：毛衣售价每降1元，平均每天可多售出2件，若商场销售这

种毛衣要求平均每天盈利达到1600元，那么每件毛衣应降价多少元？

解：设每件毛衣应降价元　　　　　　　　　　　　　　 …………1分

　　　　根据题意，得：　　　　　  …………4分

　　　　解方程，得：， 　　　　　　　　　　

　答：每件毛衣应降价10元或30元　　　　　　　　　　　 …………6分

19．（７分）光明学校的旗杆附近有一棵大树，如图所示，在某一时刻旗杆在阳光下的影子有

G

一部分在地面上(线段AB)，另有一部分在某一建筑物上(线段BC)

(1) (3分) 画出在同一时刻下大树的影子(用线段DE表示)

(2) (４分)已知旗杆的高为10米．同一时刻测得旗杆的影子AB=9.6米，BC=2米，大树的影子

DE=9米，求大树的高

解： 过点B作BH∥CG　　　　　　　　　　　　 …………1分

　　 则四边形BCGH是平行四边形

　　　∴  GH=BC=2米  AH=8米　　　　　  …………2分

∵　光线BH∥光线EF

∴　∠DEF=∠ＡBH

∵　∠EDF=∠BAG=90°

∵　△DEF≌△ABH

∴　　即

　　　 解，得： DF=7.5米

所以大树的高为7.5米　　　　　　　　　　　 …………4分

20．(７分)在△ABC中，∠B=22.5°，∠C=30°，AB的垂直平分线OD交BC边于点D，连结AD

(2)　  (３分)求∠DAC的度数

解：∵　OD垂直平分AB

∴　AD=BD

　　　 ∴　∠BAD=∠B=22.5°…………1分

　　　 　　∠ADC=∠BAD+∠B=45°…………2分

　　　 ∴　∠DAC=180°－∠ADC－∠C=105° …………3分

(2) (4分)若AC=2cm，求△ABC的面积(结果保留根号)

　　解：　作AH⊥BC于点H　　　　　　　　　　　　　　　　　　　  …………4分

　　　　  在Rt△AHC中，∠C=30°

∴　AH=AC=1cm， CH=cm　　　

∵　在Rt△ADH中，∠ADC=45°

　　　　 ∴　∠DAH=45°=∠ADC

∴　DH=AH=1cm， AD==cm　　　　　　 

　　　　　  BD=AD=cm　　　　　　　　　　　　　　　　　

　　　　 ∴　BC=（+1+）cm　　　　　　　　　　　　　　 …………6分

　　　　  所以△ABC的面积S=　　 …………7分　

21．(7分) 某医院对病房采用药薰消毒法进行消毒，已知药

物燃烧时，病房内每立方米空气中的含药量y(毫克)与时

间x(分钟)成正比例关系；药物燃烧完后，y与x成反比例

关系(如图)．药物经4分钟燃烧完毕时测得病房内每立方米

空气中的含药量为6毫克，请根据题中所提供的信息，回答

下列问题：

或

(1)(4分)药物在燃烧过程中，y与x的函数关系式为：，自变量x的取值范围是

  药物燃烧完毕后，y与x的函数关系式为：，自变量x的取值范围是；

(2)(3分)研究表明，当病房内每立方米空气中的药物含量不少于3毫克并且持续时间不低于

5分钟时，才能有效杀灭病房内的病菌，那么此次消毒是否有效？为什么？

　解：把代入,　得：秒　　　　　…………５分

把代入，　得：秒　　　　　…………６分

　　　有效杀毒时间为：８秒－２秒＝６秒＞５秒

　　　所以这次消毒是有效的。　　　　　　　　　　　…………7分

22．(10分) 如图，在Rt△ABC中，∠ACB=90°，AC=10cm，BC=15cm，点P从A出发沿AC

向C点以1厘米/秒的速度匀速移动；点Q从C出发沿CB向B点以2厘米/秒的速度匀速移

动．点P、Q分别从起点同时出发，移动到某一位置时所需时间为t秒

(3)　　(2分)当t = 4时，求线段PQ的长度

解：当t = 4时，PC=10－t=6cm　CQ=2t=8cm

　　　　在Rt△PQC中，根据勾股定理, 得:

　　　　PQ=　　　　…………2分

(4)　　(4分)当t为何值时，△PCQ的面积等于16cm²？

解：因为PC=10－t，CQ=2t

　　　　 …………4分

解方程，得：，　 …………5分

　　　　　当时，CQ=2t=16cm>15cm，超出BC的长度，应舍去

所以当秒时, △PCQ的面积等于16cm²　…………6分

(3) (4分)点O为AB的中点，连结OC，能否使得PQ⊥OC？若能，求出t的值；若不能，请说

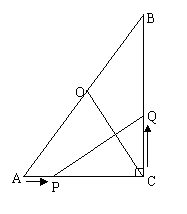明理由．

　

解：　∵　点O是斜边AB的中点

　　　　∴  OC=

∴　∠A=∠ACO　　　　　　　 …………7分

当PQ⊥OC时，∠QPC+∠ACO=90°

　　　　　　　  又　∠A+∠B=90°

　　　　∴　 ∠B=∠QPC， 同理∠A=∠PQC

∴　　△ABC∽△QPC　　　　　　 …………8分

　　　　有　　即

　　　　解，得：　　

所以当秒时，能使得PQ⊥OC。　…………10分

说明：解答题中的其它解法，请参照给分。