九年级上十二月份月考数学试卷

九年级上十二月份月考数学试卷

　　　　　　　  座位号　　　　得分　　　　　 

一、精心选一选，相信你一定能选对（每小题3分，共30分）　

1、在Rt△ABC中，各边的长度都扩大2倍，那么锐角A的正弦、余弦值………………………………………………………………………（　　）

（A）　都扩大2倍 （B） 都扩大4倍 （C）没有变化 （D） 都缩小一半

2、 在△ABC中，已知AC=3，BC=4，AB=5，那么下列结论成立的是(　　 )

A.sinA =　　　B.cosA =　　　C.tanA =　　　D.sinB =

3、 等腰三角形的一腰长为，底边长为，则其底角为 ……………………………………………………………………….（　　）

A　　　　　 B　　　　　　 C　　 　　　　D　　　

4、把抛物线y=－2x²的图象向左平移4个单位，再向上平移3个单位，所得的图象的表达式…………………………………………………………………………….（　　　）

A．y=－2（x＋4）²＋3　　　　B．y=－2（x－4）²－3

C．y=－2（x＋4）²－3　　　　D．y=－2（x－4）²＋3

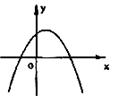5、 已知二次函数的图象如图所　 则下列结论正确的是　………………………………..　　　 （　  ）

A． 　　B．

C．　　　D．

6、如图，两个同心圆中，大圆的半径是小圆半径的2倍，把一粒

大米抛到圆形区域中，则大米落在小圆内的概率为…………….（　　　）　　　　　　　　 

A． 　　　　　　B．　　　　　　　　　 

C． 　　　　　　D．无法确定

7、某地区为估计该地区黄羊的只数，先捕捉20只黄羊给它们分别作上标志，然后放回，待有标志的黄羊完全混合于黄羊群后，第二次捕捉40只黄羊，发现其中两只有标志。从而估计该地区有黄羊……………（　　　 ）

A．200只 　　　　 B　400只　　　 C.800只　　　　　  D.1000只

8、 有两组扑克牌各三张，牌面数字均为1，2，3，随意从每组牌中各抽一张，数字和等于4的概率是………………………………………（　　 ）

A.　　 B.　　 C.　　 D.

9、某商店举办有奖储蓄活动，购货满100元者发对奖券一张，在10000张奖券中，设特等奖1个，一等奖10个，二等奖100个。若某人购物满100元，那么他中一等奖的概率是 ………………………………………（ 　　）

A、 　　B、　　  C、　　　 D、

10．函数的图象与轴有交点，则的取值范围是（　　 ）

A．　 　　　　　　　 　 B．

C．　　　　　　　　　　 D．

二、耐心填一填，相信你选的又对又快。（每小题2分，共20分）

1、任意掷一枚均匀硬币两次，两次都是同一面朝上的概率是　　　　

2、小明、小刚、小亮三人正在做游戏，现在要从他们三人中选出一人去帮王奶奶干活，则小明被选中的概率为=_____　, 小明未被选中的概率

为　　　　 

3、抛物线经过点（3，5），则 = 　　　 .

4、抛物线的顶点坐标是___________

5、计算2sin30⁰+3tan30⁰ ·tan45⁰=___________。

6、如右下图，在坡度为1︰2的山坡上种树，要求株距（相邻两树间的水平距离）是6米，斜坡上相邻两树间的坡面距离是　　　　 米．

7、某水坝迎水坡的坡度是，则它的坡角等于___________ ．

8、已知二次函数y=x²＋bx＋c，其图象的顶点为（5，－2）则b=　　　，c=　　  ．

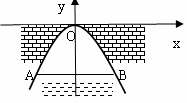9、.如图，某涵洞的截面是抛物线形，现测得水面宽是AB=1.6m,涵 洞 顶点O到水面的距离CO为2.4m,在图中直角坐标系内，涵洞截面所在　　抛物线的解析式是　　　　　 。

10．已知抛物线，请回答以下问题：

⑴　它的开口向　　　　 ，对称轴是直线　　　　　 ，顶点坐标为　　　 　 ；

⑵　图象与轴的交点为　　　　　　　　 ，与轴的交点为　　　　  。

三、细心做一做，你一定能行（每小题6分，共计30分）

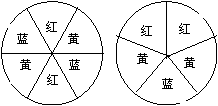
1. 如图,用树状图或表格求右面两个转盘配成紫色的概率.

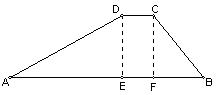
2、如图，水库大坝的横断面积是梯形，坝顶宽是，坝高为，斜坡的坡度为,斜坡的坡度为i′=1：2，求斜坡的坡角，坝度宽和斜坡的长。

3、一条抛物线经过点A（-2，0）、B（4，0）且抛物线的顶点是（1，－3），求满足此条件的函数解析式。

4、某商人如果将进货价为8元的商品按每件10元出售，每天可销售100件，现采用提高售出价，减少进货量的办法增加利润，已知这种商品每涨价1元其销售量就要减少10件，问他将售出价(x)定为多少元时，才能使每天所赚的利润(y )最大？并求出最大利润。

5、如图，海岛A四周20海里范围内是暗礁区，一艘货轮由东向西航行，在B处见岛A在北偏西，航行24海里后到C处，见岛A在北偏西，货轮继续向西航行，有无触礁危险？

四、我来解答（每小题6分，共计12分）

1、如图，在一块三角形区域ABC中，∠C=90°，边AC=8m，BC=6m，现要在△ABC内建造一个矩形水池DEFG，如图的设计方案是使DE在AB上。　

⑴求△ABC中AB边上的高h;

⑵设DG=x,当x取何值时，水池DEFG的面积(S)最大？

　　　　　　　　　　　　　　　

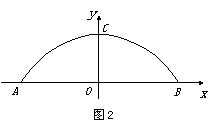
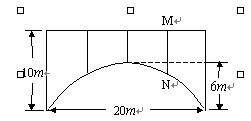
2、一座拱桥的轮廓是抛物线型(如图1所示)，拱高6，跨度20，相邻两支柱间的距离均为5；

(1) 将抛物线放在所给的直角坐标系中(如图2所示)，请根据所给的数据求出抛物线的解析式。

(2) 求支柱MN的长度.

(3) 拱桥下地平面是双向行车道(正中间是一条宽2 m的隔离带)，其中的一条行车道能否并排行驶宽2 、高3 的三辆汽车(汽车间的间隔忽略不计)？请说说你的理由

五、我来探究：（本小题8分）

如图（单位：m），等腰直角三角形ABC以2m／s的速度沿直线L向正方形移动，设xs时，三角形与正方形重叠部分的面积为ym².

（1）写出0≤t≤5时y与x的关系表达式.

（2）写出5≤t≤10时y与x的关系表达式.

（3）当x=2s，8s时，y分别是多少？

（4）当重叠部分的面积是正方形面积的一半时，三角形移动了

多长时间？