初三数学练习题（一）
（时间：120分钟 满分：150分）
一、选择题（每小题3分，共30分，每小题给出的四个选项中，只有一个符合题目要求，请把它选出来，用2B铅笔涂在答题卡上）
1、下列等式成立的是（ ）
A．
B．
C．
D．
2、方程
的解为（ ）
A．
B．
C．
D．
3、下面图案中，是中心对称图形的有（ ）
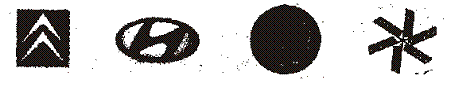
A．1个 B．2个 C．3个 D．4个
4、若直角三角形的两条直角边长分别为
、
，则它斜边上的高应为（ ）
A．
B．
C．
D．
5、如图，是一水库堤坝的截面图，已知坝高BC=6米，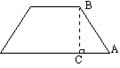
BC:AC=2:1，则斜坡AB的长是（ ）
A．
米
B．
米
C．9米 D．
米
6、如图，∠APB是⊙O的圆周角，则∠APB+∠OAB
的度数是（ ）
A．60° B．80° C．90° D．无法确定
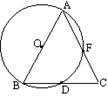
7、如图，AB是⊙O的直径，BD是弦，延长BD到点C，
使DC=BD，连结AC交⊙O于点F，则△ABC一定是不是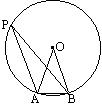
下列哪一类三角形（
）
A．等腰三角形 B．等边三角形
C．锐角三角形 D．钝角三角形
8、如图，方格纸上一圆经过（2，5），（2，-1），（-1，2），
（5，2）四点，则该圆圆心的坐标为（ ）
A．（2，-1）
B．（2，2） C．（2，1） D．（3，1）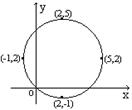
9、等腰三角形两边的长分别是方程
的两
个不相等的实数根，则这个三角形的周长是（ ）
A．8 B．10 C．8或10 D．8和10
10、如图，BC是半圆O的直径，点D是半圆上一点，
过D作⊙O的切线，BA⊥DA于点A，BA交半圆于点E，
已知BC=10，AD=4，那么直线CE与以点O为圆心，
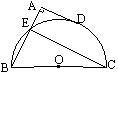
为半径的圆的位置关系是（ ）
A．相切 B．相交 C．相离 D．无法确定
二、填空题（每小题4分，共32分，将答案直接填写在题中横线）
11、使代数式
在实数范围内有意义，
的取值范围是
。
12、实数、在数轴上对应的点如图所示，
化简：
。
13、点A（-2，5）关于原点对称点的坐标为 。
14、四边形ABCD内接于⊙O，若
:
:
:
=9:7:12:8，
则四边形ABCD中最长边所对的圆心角为 度。
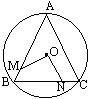
15、如图，已知⊙O的半径为5，弦AB=8，P是弦AB
上任意一点，则OP长度的取值范围是 。
16、如图，⊙A、⊙B、⊙C、⊙D、⊙E两两不相交，且半径
都为1cm，则图中的五个扇形（即阴影部分的面积）
之和为 。
17、观察下列各式
请你将猜想的规律用含自然数n（n≥1）的代数式表示出来是
。
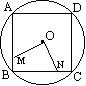
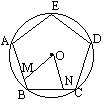
18、如图M、N分别是⊙O的内接正三角形ABC，正方形ABCD，正五边形ABCDE……、正n边形ABCDE…的边AB，BC上的点，且BM=CN，连接OM、ON。
……
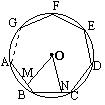⑴ ⑵ ⑶ (n)
通过研究，图⑴、⑵、⑶中∠MON度数的变化规律，你得到图(n)中∠MON的度数为 。
三、解答题（本大题共7小题，共88分，解答题应写出文字说明、证明过程或演算步骤）
19、（共12分，每小题6分）：(1)计算：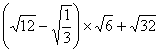
⑵已知：
求：
的值。
21、（共16分，每小题8分）⑴有一张矩形广告牌长为6米，宽为4米，现要在四周镶上宽度相同的边框，使整个面积是原来的2倍，求：镶后整个广告牌的长和宽。
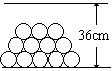
⑵超市的货架由宽为36cm的长方形隔板组成，现要在其中一层上摆放底面直径为10cm的酱油瓶，若按如图所示的两两外切方式摆放，最多能摆放几排？为什么？（参考数据：
）
22、（12分）已知关于的方程
。①当m为可值时，方程有两个实数根？②为m选择一个合适的整数，使方程有两个不相等的实数根，并求这两个实数根。③根据②的情况探索，任意一个一元二次方程
的两根
、
与系数、、
的关系为
，
=
。
22、（12分）如图，在平面直角坐标系中，△ABC的三个顶点的坐标分别是A（2，3）、
B（2，1）C（3，2）。
⑴判断△ABC的形状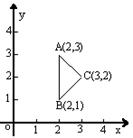
。（6分）
⑵如果将△ABC沿着边AB旋转，求所得旋转体的表面积。（6分）
23、（12分）如果一个三角形的三边长分别为a、b、c，设
，则三角形面积为
称为海伦公式，现有一块三角形铁板△ABC，AB=6，BC=5，AC=4，要用此三角形铁板切割出一个圆形工件。
⑴用尺规作图方法，画出所能切割出的最大的圆形工件示意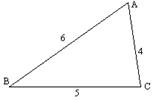
图。（不写画法，保留画图痕迹）（4分）
⑵试计算此最大圆形工件的面积。
24、（12分）如图，已知AD是∠ABC的平分线，以AB上一点O为圆心，AD为弦作⊙O。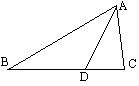
⑴若BC恰为⊙O的切线，则△ABC是什么三角形？（4分）
⑵在所给图中作出与BC边相切的⊙O（不写作法，保留作图痕迹）；（3分）
⑶若在上述条件下AC=3，∠B=30°，求⊙O与△ABC重叠部分的面积。（5分）
25、（12分）如图A（-1，0），B（m，0）（m>0）的横坐标是一元二次方程
的两个根，⊙M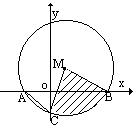
经过A，B两点，并与
轴交于负半轴上的C点，AC的长为
。
⑴试探究a、b之间的数量关系；（6分）
⑵欲使图中阴影部分扇形的面积S不小于6
，求m的最小整数值。（6分）