初三数学月考卷 班级 姓名 学号
一、选择题(每小题3分)
1、在![]() 中,
中,![]() ,AB=15,sinA=
,AB=15,sinA=![]() ,则BC等于( )
,则BC等于( )
A、45 B、5 C、![]() D、
D、![]()
2、李红同学遇到了这样一道题:![]() tan(α+20°)=1,你猜想锐角α的度数应是(
)
tan(α+20°)=1,你猜想锐角α的度数应是(
)
A.40° B.30° C.20° D.10°
3、如果![]() ,那么
,那么![]() 等于……………………………………………… ( )
等于……………………………………………… ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
4.如果两个相似三角形的相似比为1:4,那么它们的周长比为…………( )
(A)1:16 (B)1:8 (C)1:4 (D)1:2
5.如图所示,在长为8cm,宽为6cm的矩形中,截去一个矩形(图中阴影部分),如果剩下矩形与原矩形相似,那么剩下矩形的面积是………………………… ( )
 A.28cm2
B.27cm2 C.21cm2 D.20cm2
A.28cm2
B.27cm2 C.21cm2 D.20cm2
(第5题) (第6题)
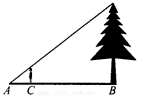
6.如图,身高为1.6m的某学生想测量一棵大树的高度,他沿着树影BA由B点向A点走去,当走到C点时,他的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,则树的高度为……………………………………………………( )
(A)4.8m (B)6.4m (C)8m (D)10m
7. 在平面直角坐标系中,以点(2 , l)为圆心、1为半径的圆必与( )
A. x轴相交 B.y轴相交 C. x轴相切 D. y轴相切
8.已知⊙O1与⊙O2内切,它们的半径分别为2和3,则这两圆的圆心距d满足( )
 (A)d=5 (B)d=1 (C)1<d<5 (D)d >5
(A)d=5 (B)d=1 (C)1<d<5 (D)d >5
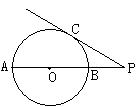
9.如图,AB是⊙O的直径,P是AB延长线上的一点,
PC切⊙O于点C,PC=3、PB:AB=1:3,则⊙O的半
径等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]() (第9题)
(第9题)
 10.如图,在矩形ABCD中,E是AD边上的点,且∠BEC=Rt∠,
10.如图,在矩形ABCD中,E是AD边上的点,且∠BEC=Rt∠,
AE=5,ED=4,则CE的长是………………………………( )
(A)5 (B) 6 (C) 7 (D)7.5
 二、填空题(每小题3分)
二、填空题(每小题3分)
1.如图,PA、PB是⊙O的切线,A、B为切点,若
∠APB=60°,则∠ABO= .
|
 ⊙A与BC相切于点D,则⊙A的半径为 cm.
⊙A与BC相切于点D,则⊙A的半径为 cm.
3.数3和12的比例中项是 。
4.若点P是线段AB的黄金分割点,且AP >BP,AB=2,
|
 5.如图,在△ABC中,请添加一个条件:
,
5.如图,在△ABC中,请添加一个条件:
,
使 △ACD∽△ABC。
|
 7、在△ABC中,AB=AC=10,BC=16,则tanB=_____。
7、在△ABC中,AB=AC=10,BC=16,则tanB=_____。
8、菱形的两条对角线长分别为2![]() 和6,则菱形较小的内角为______度。
和6,则菱形较小的内角为______度。
|
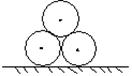 10、如图9,施工工地的水平地面上有三根外径都是2米的水泥管,两两相切地堆放在一起,则其最高点到地面的距离是
.
10、如图9,施工工地的水平地面上有三根外径都是2米的水泥管,两两相切地堆放在一起,则其最高点到地面的距离是
.
|
1.计算题(每题6分)
(1)![]() sin30°+
sin30°+![]() sin45°
(2)6tan2 60°-
sin45°
(2)6tan2 60°-![]() sin 60°-2cos30°
sin 60°-2cos30°
2. 如图7,在Rt△ABC中,∠C=90°,AC=8,∠A的平分线AD=![]()
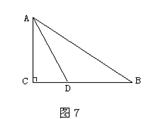 求∠B的度数及边BC、AB的长.(6分)
求∠B的度数及边BC、AB的长.(6分)
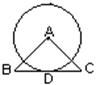
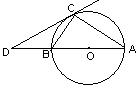 3.(本题6分)如图,△ABC中,∠BCA=90°,∠A=30°,以AB为直径画⊙O,延长AB到D,使BD等于⊙O的半径.
3.(本题6分)如图,△ABC中,∠BCA=90°,∠A=30°,以AB为直径画⊙O,延长AB到D,使BD等于⊙O的半径.
求证:CD是⊙O的切线.
4.(本题8分)如图,在梯形ABCD中,AD∥BC,对角线AC与BD相交于点O,过点O作OE∥AD交AB于点E,若AD=6cm,BC=12cm,△AOD的面积为6cm![]() ,
,
 (1)求△BOC和△DOC的面积;
(1)求△BOC和△DOC的面积;
(2)求OE的长。
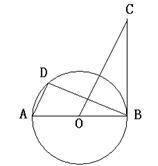
5. (本题8分)如图,AB是⊙O的直径,BC是⊙O的切线,
D是⊙O上一点,且AD∥OC
(1)求证:△ADB∽△OBC
(2)若AB=2,BC=![]() ,求AD的长(结果保留根号)
,求AD的长(结果保留根号)
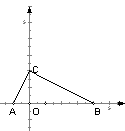 6.如图,已知在△RtABC中,∠ACB=Rt∠,以斜边上的高线CO与斜边AB为轴建立直角坐标系,已知OA=1,AC=
6.如图,已知在△RtABC中,∠ACB=Rt∠,以斜边上的高线CO与斜边AB为轴建立直角坐标系,已知OA=1,AC=![]() ,
,
求经过A、B、C三点的抛物线的解析式;(6分)
加试题
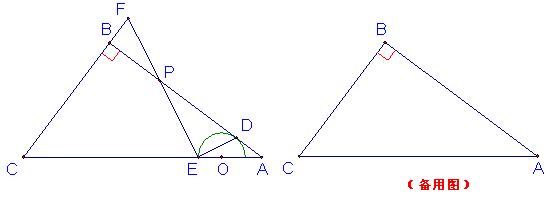
在△ABC中,∠ABC=90°,AB=4,BC=3,O是边AC上的一个动点,以点O为圆心作半圆,与边AB相切于点D,交线段OC于点E,作EP⊥ED,交射线AB于点P,交射线CB于点F。
(1) 如图,求证:△ADE∽△AEP;
(2) 设OA=x,AP=y,求y关于x的函数解析式,并写出x的取值范围;
(3) 当BF=1时,求线段AP的长.
![]()