初三数学周周清（十一）
命题人：李跃平
时间：90分 满分：100分 姓名
一、填空题（每空2分，共20分）
1、若
是二次函数，则m＝
2、抛物线y=－x2＋4x＋ｃ的最大值等于3，则ｃ=
3、已知二次函数y=-x2+2x+c2的对称轴与x轴交于点（m,0）,则m的值为
4、一条抛物线的对称轴是x=1，且与x轴有唯一的公共点、开口方向向下，则这条抛物线的解析式是 （任写一个）
5、抛物线
的对称轴是x=2，且过点（3,0），则a+b+c=
6、二次函数y=x2-2x-3与x轴两交点之间的距离为
7、二次函数
的图象如图所示，则一次函数y=ax+bc的图象不过第 象限
8、将抛物线
先向右平移1个单位，再绕顶点旋转180°，所得抛物线的解析式是
9、抛物线y=x2-4x-5交x轴于A、B两点，交y轴于点C，则△ABC面积为 。
10、汽车刹车距离s(m)与速度v(km/h)之间的函数关系是
，在一辆车速为100km/h的汽车前方120m处，发现停放一辆故障车，此时刹车 有危险（填“会”或“不会”）
二、选择题（每小题3分，共30分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
1、二次函数y=kx2-3x+2k- k2图象过原点，则k的值：
A、2 B、0 C、2或0 D、不能确定
2、二次函数y=a(x-k)2+k(a
)不论k取何实数时，图象的顶点一定在
A、直线y=－x上； B、直线y=x上 C、x轴上 D、y轴上
3、若二次函数过原点和第一、二、三象限，则
A、a>0,b>0,c=0; B、a>0,b<0,c=0; C、a<0,b>0,c=0 D、a<0,b<0,c=0
4、从y=x2的图象可看出，当－3≤ｘ≤－1时，ｙ的取值范围是
A、ｙ≤0或
B、0≤ｙ≤9 C、0≤ｙ≤1 D、1≤ｙ≤9
5、二次函数y=(k-1)x2-2kx+k+3的图象与x轴无交点，且抛物线的开口向上，则k的取
值范围 A、k＜1 B、k＞3/2 C、1<k<3/2 D、k>3/2或k<1
6、已知抛物线y=kx2-7x-7与x轴有交点，则k的取值范围是
A、
B、
C、
D、
7、在同一坐标系中，函数
的图象大致是
8、若一元二次方程ax2+bx+c＝0的两根是－3和1，那么二次函数y= ax2+bx+c的图象的对称轴是直线 A、x=-3 B、x=-2 C、x=-1 D、x=1
9、二次函数y=2x2+bx-5(b<0)的顶点在
A、第一象限 B、第二象限 C、第三象限 D、第四象限
10、无论m为任何实数，二次函数y=x2+(2-m)x+m的图象总过点
A、(-1，3) B、(1，0) C、(1，3) D、(-1，0)
三、解答题
1、（5分）已知矩形的周长为36cm，矩形绕它的一边旋转形成一个圆柱，矩形的长、宽各为多少时，旋转形成的圆柱的侧面积最大？
2、（8分）二次函数y=－3x2－2x+c的顶点A在直线
上,且直线与x轴的交点为B ① 求函数解析式 ② 求出△OAB的面积
3、（8分）已知二次函数y=-x2+(m－1)x+m与y轴交于点（0,3）
（1） 求出m的值并画出这条抛物线；
（2） 求它与x轴的交点和抛物线顶点的坐标；
（3） x取何值时，抛物线在x轴的上方？
（4） x取何值时，y随x的增大而减小？
4、（6分）如图，一抛物线型拱桥，拱顶离水面高4米，水面宽度AB＝10米。现有一竹排运送一只货箱欲从桥下经过，已知货箱长10米，宽6米，高2.25米（竹排与水平面持平），问该货箱是否顺利通过该桥？
5、（12分）忻州汽车城销售某种型号的汽车，每辆进货价为25万元，市场调研表明：当销售价为29万元时，平均每周能售出8辆；而当销售价每降低0.5万元时，平均每周能多售出4辆。如果设每辆汽车降价x万元，每辆汽车的销售利润为y万元。
（1） 求y与x的函数关系式；在保证商家不亏本的前提下，写出x的取值范围；
（2） 假设这种汽车平均每周的销售利润为W万元，试写出W与x的函数关系式；
（3） 当每辆车的定价为多少万元时，平均每周的销售利润最大？最大利润是多少？
6、（11分）心理学家研究发现，一般情况下，学生的注意力随着教师讲课时间的变化而变化，讲课开始时，学生的注意力逐步增强，中间有一段时间学生的注意力保持较为理想的状态，随后学生的注意力开始分散，经过实验分析可知，学生的注意力y随时间t的变化规律有如下解析式：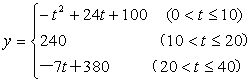
(1) 讲课开始后第5分钟时与讲课后第25分钟时比较，何时学生的注意力更集中？
(2) 讲课开始后多少分钟，学生的注意力最集中？能持续多少分钟？
(3) 一道数学难题，需要讲解24分钟，为了效果较好，要求学生的注意力最低达到180，那么经过适当安排，老师能否在学生注意力达到所需的状态下讲解完这道题目？