26.1 二次函数(三)
一、双基整合:
1.抛物线y=20-![]() x2可以看作抛物线y=______沿y轴向______平移_____个单位得到的.
x2可以看作抛物线y=______沿y轴向______平移_____个单位得到的.
2.抛物线y=-3x2上两点A(x,-27),B(2,y),则x=_______,y=_______.
 3.抛物线y=-
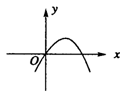
3.抛物线y=-![]() x2-3的图象开口_____,对称轴是_____,顶点坐标为________,当x=________时,y有最_____值为________.
x2-3的图象开口_____,对称轴是_____,顶点坐标为________,当x=________时,y有最_____值为________.
4.若二次函数y=ax2+bx+a2-1(a≠0)的图像如图所示,则a的值是________.
5.二次函数y=x2的图象向上平移2个单位,得到新的图象的二次函数表达式是( )A.y=x2-2 B.y=(x-2)2 C.y=x2+2 D.y=(x+2)2
6.函数y=ax2-a与y=![]() (a≠0)在同一直角坐标系的图象可能是( )
(a≠0)在同一直角坐标系的图象可能是( )
 7.二次函数y=mx2+m-2的图象的顶点在y轴的负半轴上,且开口向上,则m的取值范 围为( )A.m>2 B.m<2 C.0<m<2 D.m<0
7.二次函数y=mx2+m-2的图象的顶点在y轴的负半轴上,且开口向上,则m的取值范 围为( )A.m>2 B.m<2 C.0<m<2 D.m<0
8.二次函数的图象如图所示,则它的解析式为( )
A.y=x2-4 B.y=4-x2 C.y=![]() (4-x2) D.y=
(4-x2) D.y=![]() (2-x2)
(2-x2)
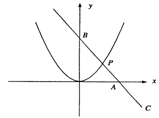 9.如图所示,直线L过A(4,0)和B(0,4)两点,它与二次函数y=ax2的图象在第一象限内交于P点,若△AOP的面积为
9.如图所示,直线L过A(4,0)和B(0,4)两点,它与二次函数y=ax2的图象在第一象限内交于P点,若△AOP的面积为![]() .(1)求P点的坐标;
.(1)求P点的坐标;
(2)求二次函数的解析式;
(3)能否将抛物线y=ax2平移,使平移后的抛物线经过点A?
二、探究创新
10.若二次函数y=ax2+c,当x取x1,x2(x1≠x2)时,函数值相等,则当x取x1+x2时,函数值为( ) A.a+c B.a-c C.-c D.c
11.对于反比例函数y=-![]() 与二次函数y=-x2+3,请说出它们的两个相同点,再说出它们的两个不同点.
与二次函数y=-x2+3,请说出它们的两个相同点,再说出它们的两个不同点.
12.如图,宜昌西陵长江大桥属于抛物线形悬索桥,桥面(视为水平的)与主悬钢索之间用竖直钢拉索连接,桥两端主塔塔顶的海拔高度均是187.5米,两主塔之间的距离为900米,这里水面的海拔高度是74米.
若过主塔塔顶的主悬钢索(视为抛物线)的最低点离桥面的高度为0.5米,桥面离水面的高度为19米,请你计算距离桥两端主塔100米处竖直钢拉索的长.(结果精确到0.1米)

三、智能升级
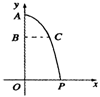 13.今年夏季我国部分地区遭受水灾,空军某部奉命赶赴灾区空投物资,已知空投物资离开飞机后在空中沿抛物线降落,抛物线的顶点在机舱口A处,如图.
13.今年夏季我国部分地区遭受水灾,空军某部奉命赶赴灾区空投物资,已知空投物资离开飞机后在空中沿抛物线降落,抛物线的顶点在机舱口A处,如图.
(1)如果空投物资离开A处后下落的垂直高度AB=160米时,它到A处的水平距离为BC=200米,那么要使飞机在垂直高度AO=1000米的高空进行空投,物资恰好准确落在P处,飞机到P处的水平距离OP为多少米?
(2)如果根据空投时的实际风力和风向测算,当空投物资离开A处的垂直距离为160米时,它到A处的水平距离为400米,要使飞机仍在(1)中O点的正上方空投,且使空投物资准确地落在P处,那么飞机空投的高度应调整为多少米?
26.1 二次函数(二)
一、双基整合:1.二次函数y=mx![]() 的图象有最高点,则m=______.
的图象有最高点,则m=______.
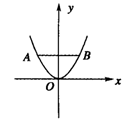
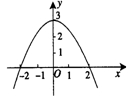
 2.二次函数的图象如图1所示,则它的解析式为____________,如果另一函数图象与该图象关于x轴对称,那么它的解析式是______________.
2.二次函数的图象如图1所示,则它的解析式为____________,如果另一函数图象与该图象关于x轴对称,那么它的解析式是______________.
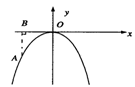
3.如图2所示,点A是抛物线
y=-x2上一点,AB⊥x轴于B,若B点坐标为(-2,0),则A点坐标为______,S△AOB______.
4.抛物线y=x2与双曲线y=![]() 的交点A的坐标为________.
的交点A的坐标为________.
5.在同一坐标系中,抛物线y=4x2,y=![]() x2,y=-
x2,y=-![]() x2的共同特点是( )
x2的共同特点是( )
A.关于y轴对称,抛物线开口向上; B.关于y轴对称,y随x的增大而增大
C.关于y轴对称,y随x的增大而减小; D.关于y轴对称,抛物线顶点在原点
6.下列关于抛物线y=x2和y=-x2的关系的说法错误的是( )
A.它们有共同的顶点和对称轴; B.它们都关于y轴对称;
C.它们的形状相同,开口方向相反; D.点A(-2,4)在抛物线y=x2上也在抛物线y=-x2上
7.已知h关于t的函数关系式为h=![]() gt2(t为正常数,t为时间),则函数图象为( )
gt2(t为正常数,t为时间),则函数图象为( )
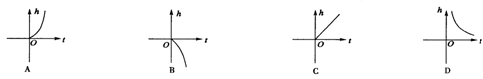
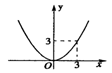
8.如图3,A,B分别为y=x2上两点,且线段AB⊥y轴,若AB=6,则直线AB的表达式为( )A.y=3 B.y=6 C.y=9 D.y=36
9.正方形的边长为xcm,面积为Scm2.
(1)写出S与x的函数关系式,指出自变量x的取值范围;
(2)画出S随x的变化而变化的图象;
(3)设正方形的边长增加2cm2时,面积增加ycm2,你能画出y随x的变化而变化的图象吗?
二、探究创新
10.二次函数y=-![]() x2,当x1>x2>0时,则y1与y2的大小关系是_________.
x2,当x1>x2>0时,则y1与y2的大小关系是_________.
11.已知二次函数y=mx![]() 中,当x>0时,y随x的增大而增大,则m=________.
中,当x>0时,y随x的增大而增大,则m=________.
12.已知a<-1,点(a-1,y1),(a,y2),(a+1,y2)都在函数y=x2的图象上,则( ) A.y1<y2<y3 B.y1<y3<y2 C.y3<y2<y1 D.y2<y1<y3
13.已知二次函数y=ax2经过点A(-2,4)(1)求出这个函数关系式;
(2)写出抛物线上纵坐标为4的另一个点B的坐标,并求出S△AOB;
(3)在抛物线上是否存在另一个点C,使得△ABC的面积等于△AOB面积的一半?如果存在,求出点C的坐标;如果不存在,请说明理由.
三、智能升级
14.若点P(1,a)和Q(-1,b)都在抛物线y=-x2上,则线段PQ的长是______.
15.汽车刹车距离s(m)与速度V(km/h)之间的函数关系是S=![]() V2,在一辆车速为100km/h的汽车前方80m处,发现停放一辆故障车,此时刹车______有危险.(填“会”或“不会”)
V2,在一辆车速为100km/h的汽车前方80m处,发现停放一辆故障车,此时刹车______有危险.(填“会”或“不会”)
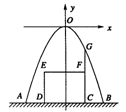 16.如图所示,有一城门洞呈抛物线形,拱高为4m(最高点到地面的距离),把它放在直角坐标系中,其解析式为y=-x2.
16.如图所示,有一城门洞呈抛物线形,拱高为4m(最高点到地面的距离),把它放在直角坐标系中,其解析式为y=-x2.
(1)求城门洞最宽处AB的长;
(2)现在有一高2.6m,宽2.2m的小型运货车,问它能否完全通过此城门?